Burada arkkotanjantın türevinin formülünü bulacaksınız ve bir fonksiyonun arkkotanjantının nasıl türetileceğini örneklerle açıklayacağız.
arkkotanjant türev formülü
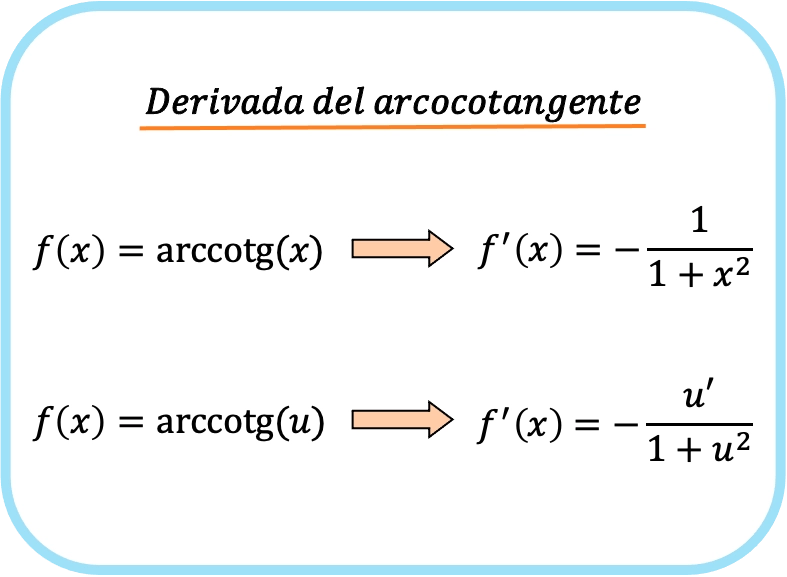
X’in arktanjantının türevi negatif bir bölü bir artı x karedir.
![]()
Bu nedenle, bir fonksiyonun arkkotanjantının türevi, eksi o fonksiyonun türevinin bir artı kare fonksiyonuna bölünmesine eşittir.
![]()
Birinci ve ikinci formüllerin aynı olduğuna dikkat edin, tek fark ikinci ifadeye zincir kuralının uygulanmasıdır. Aslında u yerine x koyarsanız x fonksiyonunun türevi 1 olduğundan ilk formülü elde edersiniz.
Arkotanjant kotanjantın ters fonksiyonu olmasına rağmen türevleri oldukça farklıdır. Aslında bir fonksiyonun kotanjantının türetilmesinin üç yolu vardır; bunların hepsini burada görebilirsiniz:
➤ Bakınız: kotanjantın türevinin formülü
Arkotanjantın türevi örnekleri
Arkotanjantın türevinin formülünün ne olduğunu gördükten sonra, bu tür trigonometrik türevin çözülmüş iki alıştırmasını burada bulabilirsiniz. Ayrıca sorularınız olursa aşağıya yorum olarak bırakabileceğinizi de unutmayın.
örnek 1
Bu örnekte ikinci dereceden x 2 fonksiyonunun arkkotanjantının türevinin ne kadar olduğunu göreceğiz.
![]()
Arkotanjant argümanında x dışında bir fonksiyonumuz var, dolayısıyla arkkotanjantın türevi formülünü zincir kuralıyla uygulamamız gerekiyor:
![]()
X’in ikiye yükseltilmiş türevi 2x’tir, dolayısıyla paya 2x’i ve paydaya kare argümanının fonksiyonunu koymalıyız:
![]()
Örnek 2
Bu ikinci örnekte üçüncü dereceden bir polinom fonksiyonunun arkkotanjantını türeteceğiz.
![]()
Türetilmesini gerçekleştirmek için arkkotanjant türev kuralını kullanırız:
![]()
Dolayısıyla fonksiyonun arkkotanjantının türevi şöyledir:
![]()