Bu makalede bir fonksiyonun arktanjantının nasıl türetileceğini öğreneceksiniz. Ayrıca bu tür türev örneklerini görebileceksiniz ve hatta arktanjantın türevi üzerine çözülmüş alıştırmalar yapabileceksiniz. Son olarak arktanjantın türevinin formülünün ispatını da gösteriyoruz.
Arktanjantın türevi nedir?
X’in arktanjantının türevi bir bölü bir artı x’in karesidir.
![]()
Bu nedenle, bir fonksiyonun arktanjantının türevi, o fonksiyonun türevinin bir artı adı geçen fonksiyonun karesine bölünmesine eşittir.
![]()
Bu durumda fonksiyon au ile temsil ediliyordu, yani u fonksiyonunun arktanjantının türevinin formülü bu olurdu.
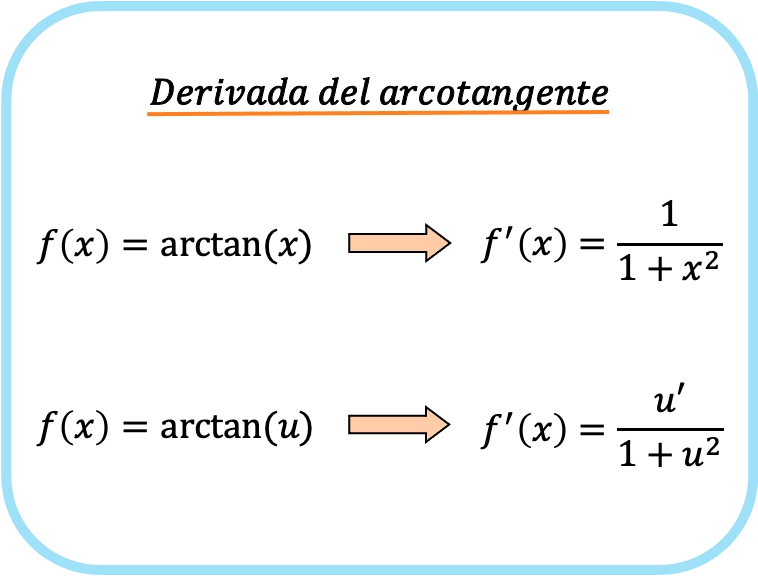
Gördüğünüz gibi, ters tanjantın türevinin formülü, arksinüs ve arkkosinüs türevlerinin formüllerine çok benzer.
Arktanjant türevi örnekleri
Arktanjantın türevinin formülünü öğrendikten sonra, bu tip trigonometrik türevlerin çeşitli örneklerinin türetilmesini açıklayacağız. Bu şekilde bir fonksiyonun arktanjantının nasıl türetildiğini anlamanız daha kolay olacaktır.
Örnek 1: 2x’in arktanjantının türevi
![]()
Türevi çözmek için formülü uyguluyoruz:
![]()
2x’in türevi 2’dir, yani 2x’in arktanjant türevi 2 bölü bir artı 2x karedir:
![]()
Örnek 2: x karenin arktanjantının türevi
![]()
Bu örneğin türevinin sonucunu bulmak için arktanjantın türevinin formülünü kullanmamız gerekir:
![]()
Dolayısıyla, x 2 fonksiyonunun türevi 2x’tir, yani x’in arktanjantının 2’ye yükseltilmiş türevi şöyledir:
![]()
Örnek 3: Sinüs x’in arktanjantının türevi
![]()
Mantıksal olarak türevi hesaplamak için ilgili formülü uygulamanız gerekir:
![]()
Bu durumda bileşik bir fonksiyonumuz var, dolayısıyla arktanjantın türevini hesaplamak için zincir kuralını uygulamamız gerekiyor:
![]()
Arktanjantın türevine ilişkin çözülmüş alıştırmalar
Aşağıdaki arktanjant fonksiyonlarını türetin:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
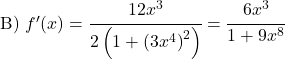
![]()
![]()
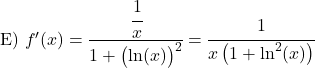
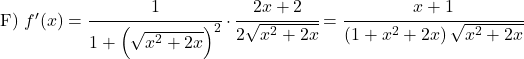
Arktanjant türevinin formülünün gösterilmesi
Daha sonra arktanjantın türevinin formülünü kanıtlayacağız.
![]()
Arktanjantın, tanjantın ters fonksiyonu olması gerçeğinden yararlanarak ilk olarak arktanjantı bir teğete dönüştürüyoruz:
![]()
Denklemin iki tarafını farklılaştırıyoruz:
![]()
Siliyoruz ve’:
![]()
Öte yandan, temel trigonometrik özdeşlik sayesinde sinüs ve kosinüsün karelerinin toplamının 1’e eşit olduğunu biliyoruz. Dolayısıyla önceki ifadeyi kesire dönüştürebiliriz:
![]()
![]()
Tüm terimleri kosinüsün karesine bölüyoruz:
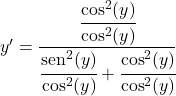
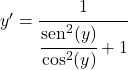
Sinüs bölü kosinüs teğete eşittir, yani:
![]()
![]()
Yukarıda gördüğümüz gibi, tanjant x değişkenine eşdeğerdir, dolayısıyla arktanjantın türevinin formülüne ulaşmak için ifadeyi değiştirebiliriz:
![]()