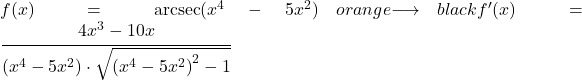Arsekant türevi

Bu sayfada arksekantın (formül) türevinin ne olduğunu göreceksiniz. Bir fonksiyonun arksekantının türevlerine ilişkin çözümlü alıştırmalar bulacaksınız.

Arsekant türevi formülü

X’in arksekantının türevi, bir bölü x çarpı kök x kare eksi 1’in çarpımıdır.

f(x)=\text{arcsec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x\cdot \sqrt{x^2-1}}

Bu nedenle, bir fonksiyonun arksekantının türevi, o fonksiyonun türevinin bölümünün fonksiyon çarpı o fonksiyonun kökünün karesi eksi bire bölünmesine eşittir.

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Açıkçası ikinci formül birinci formüle benzer, ikisi arasındaki tek fark ikinci formülde zincir kuralının uygulanmasıdır.

arksekantın türevi

Ters fonksiyonlar oldukları için tuhaf görünse de arksekantın türevinin sekantın türeviyle hiçbir ilgisi yoktur. Sekantın türevinin formülünü buraya tıklayarak görebilirsiniz:

➤ Bakınız: sekantın türevi

Arsekant türevi örnekleri

örnek 1

Bu örnekte doğrusal fonksiyonun 7x arksekantının türevinin ne kadar olduğunu göreceğiz.

f(x)=\text{arcsec}(7x)

Arsekantın türevini bulmak için aşağıdaki gibi karşılık gelen formülünü uygulamanız gerekir:

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

7x fonksiyonunun türevi 7’dir, dolayısıyla 7x fonksiyonunun arksekantının türevi şöyledir:

f(x)=\text{arcsec}(7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{7}{7x\cdot \sqrt{(7x)^2-1}}=\cfrac{1}{x\cdot \sqrt{49x^2-1}}

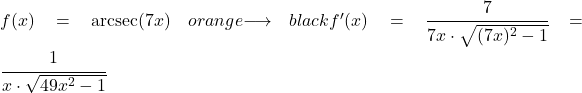
Örnek 2

Bu ikinci örnekte potansiyel bir fonksiyonun arksekantını türeteceğiz.

f(x)=\text{arcsec}(x^4-5x^2)

Yaysekant fonksiyonunun argümanında x dışında bir terim olduğundan, fonksiyonun tamamını türetmek için yaysekant türev kuralını zincir kuralıyla birlikte uygulamamız gerekir.

f(x)=\text{arcsec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Yani payda fonksiyonun argümanının türevini yazıyoruz ve paydada potansiyel fonksiyonu yeniden yazıyoruz ve bunu 2 eksi 1’in gücüne yükseltilmiş argümanın fonksiyonunun kareköküyle çarpıyoruz:

f(x)=\text{arcsec}(x^4-5x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{4x^3-10x}{(x^4-5x^2)\cdot \sqrt{\left(x^4-5x^2\right)^2-1}}

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top