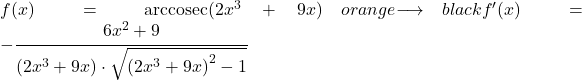Kosekant yayının türevi

Bu sayfada arkkozantın türevinin formülünün ne olduğunu göreceksiniz. Ayrıca bir fonksiyonun yay kosekantının türevlerine ilişkin çözülmüş alıştırmaları da görebileceksiniz.

Arccosekant türevi formülü

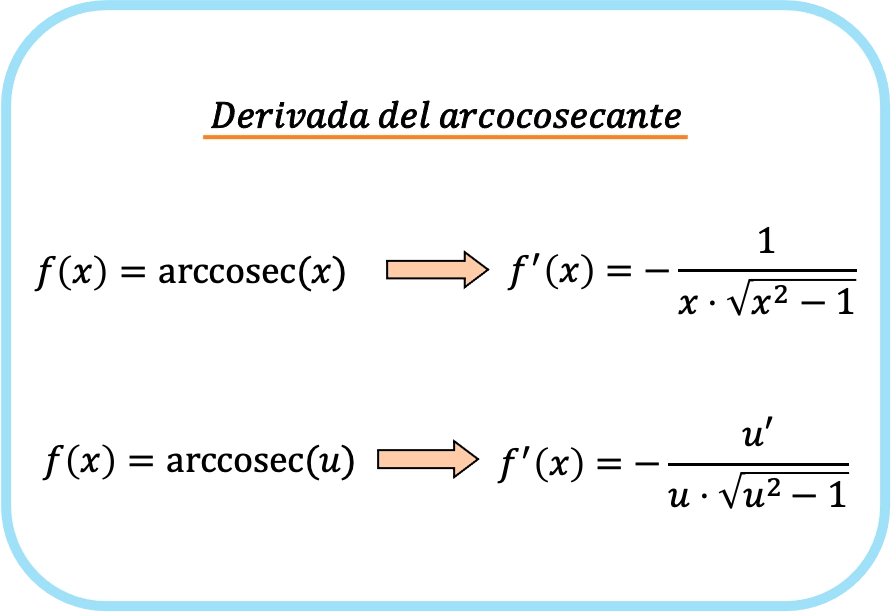
X’in arkkozekantının türevi negatif bir bölü x çarpı kök x kare eksi 1’in çarpımıdır.

f(x)=\text{arccosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{x\cdot \sqrt{x^2-1}}

Bu nedenle, bir fonksiyonun yay kosekantının türevi, eksi o fonksiyonun türevinin bölümü, fonksiyon çarpı o fonksiyonun kökünün karesi eksi bire eşittir.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Aslında önceki iki formül aynı ancak ikinci ifadede zincir kuralı uygulanıyor. Aslında, x’in birim fonksiyonunu u’da yerine koyarsanız, x’in türevi bir olduğundan, x’in arkkosekantının türevini elde edersiniz.

arkkozakant türetilmiş formül

Bildiğiniz gibi arkkosekant, kosekantın ters trigonometrik fonksiyonudur ancak türevleri oldukça farklıdır. Bu diğer trigonometrik fonksiyon türünün formülünü aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız:kosekantın türevi

Kosekant yayın türevi örnekleri

Arkosekant türev kuralının ne olduğunu görerek, bu türevin iki örneğini çözeceğiz. Ancak kosekant yayının nasıl türetileceği konusunda hala sorularınız varsa yorumlarda bize sorabilirsiniz.

örnek 1

Bu örnekte ikinci dereceden x 2 fonksiyonunun yay kosekantının türevinin ne kadar olduğunu göreceğiz.

f(x)=\text{arccosec}(x^2)

X karenin arkkozakantının türevini hesaplamak için yukarıda gördüğümüz formülü uyguluyoruz:

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

x üzeri ikinin türevi 2x olduğundan bileşik fonksiyonun türevi şöyle olur:

f(x)=\text{arccosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{x^2\cdot \sqrt{\left(x^2\right)^2-1}}=-\cfrac{2x}{x^2\cdot \sqrt{x^4-1}}

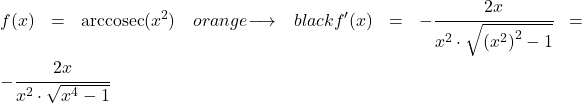
Örnek 2

Bu ikinci örnekte potansiyel bir fonksiyonun arkkozantını türeteceğiz.

f(x)=\text{arccosec}(2x^3+9x)

Tüm fonksiyonun türevini bulmak için arksekant türev kuralını kullanmamız gerekir.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

Yani payda fonksiyonun argümanının türevini yazıyoruz ve paydada potansiyel fonksiyonu yeniden yazıyoruz ve bunu argümanın fonksiyonunun karesi eksi 1’in kareköküyle çarpıyoruz:

f(x)=\text{arccosec}(2x^3+9x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{6x^2+9}{(2x^3+9x)\cdot \sqrt{\left(2x^3+9x\right)^2-1}}

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top