Bu sayfada antisimetrik matrislerin ne olduğunu açıklıyoruz. Ayrıca, onu mükemmel bir şekilde anlamak için çeşitli örneklerin yanı sıra tipik yapısını da görebileceksiniz. Ayrıca antisimetrik bir matrisin determinantını hesaplamanın özelliğini ve bu tip matrisin tüm özelliklerini açıklıyoruz. Ve son olarak, herhangi bir kare matrisi, bir simetrik matris artı başka bir antisimetrik matrisin toplamına nasıl ayrıştıracağınızı keşfedeceksiniz.
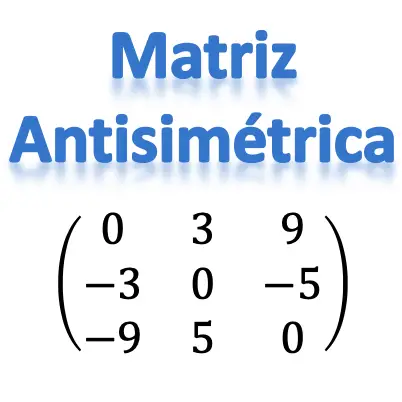
Antisimetrik matris nedir?
Antisimetrik matrisin tanımı aşağıdaki gibidir:
Antisimetrik bir matris, transpozu matrisin negatifine eşit olan bir kare matristir.
![]()
Altın
![]()
transpoze matrisini temsil eder
![]()
Ve
![]()
matris
![]()
tüm unsurlarıyla birlikte işaret değişti.
Antisimetrik matris örnekleri
Antisimetrik matris kavramını öğrendikten sonra, onu daha iyi anlamak için birkaç antisimetrik matris örneği göreceğiz:
2 × 2 mertebesinde bir antisimetrik matris örneği
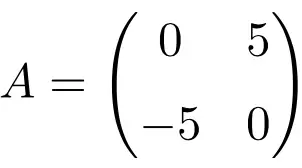
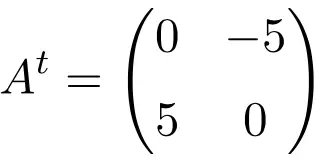
3×3 boyutlu antisimetrik matris örneği
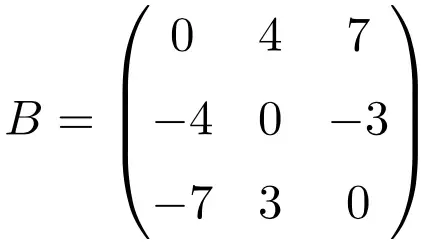
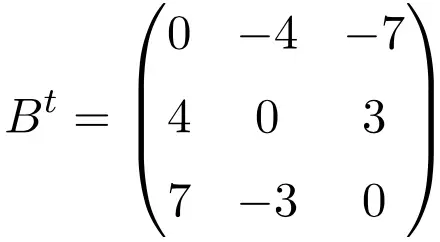
4 × 4 boyutunda bir antisimetrik matris örneği
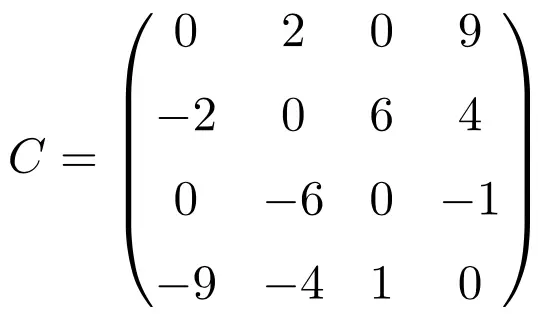
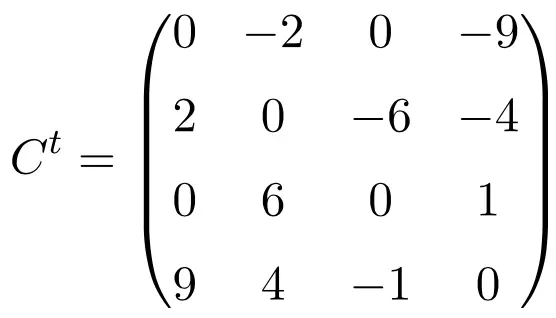
Bu üç matrisin transpozisyonunu yaparken bunların antisimetrik olduklarını doğrularız çünkü transpoze edilmiş matrisler ilgili orijinal matrislerin değişen işaretlerine eşdeğerdir.
Antisimetrik bir matrisin yapısı
Antisimetrik matris koşulunun karşılanması için, bunların her zaman aynı tip yapıya sahip olmaları gerekir: ana köşegendeki sayıların tümü sıfıra eşittir ve i . satır ile j sütununun elemanı, j satırı ve sütununun elemanının negatifidir. ben . Başka bir deyişle antisimetrik matrislerin formu aşağıdaki gibidir:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21250d80d061affcf74ef1338b4d1314_l3.png)
Bu nedenle, antisimetrik bir matrisin ana köşegeni, antisimetrinin ekseni görevi görür. Bu özel matrisin adı buradan gelmektedir.
Antisimetrik bir matrisin determinantı
Antisimetrik bir matrisin determinantı söz konusu matrisin boyutuna bağlıdır. Bu, belirleyicilerin özelliklerinden kaynaklanmaktadır:
![]()
Dolayısıyla antisimetrik matris tek sıralıysa determinantı 0’a eşit olacaktır . Öte yandan antisimetrik matris eşit boyutlu ise determinant herhangi bir değeri alabilir.
Bu nedenle, tek boyutlu bir antisimetrik matris, tekil veya dejenere bir matristir. Öte yandan, çift sıralı bir antisimetrik matris düzenli bir matristir.
Antisimetrik matrislerin özellikleri
Antisimetrik matrislerin özellikleri aşağıdaki gibidir:
- İki antisimetrik matrisin eklenmesi (veya çıkarılması) başka bir antisimetrik matris verir. Toplanan (veya çıkarılan) iki matrisin transpozisyonunun her matrisin ayrı ayrı transpozisyonuna eşdeğer olması nedeniyle:
![]()
- Herhangi bir antisimetrik matrisin bir skalerle çarpılması aynı zamanda başka bir antisimetrik matrisin ortaya çıkmasına neden olur.
- Antisimetrik bir matrisin gücü, bir antisimetrik matrise veya simetrik bir matrise eşdeğerdir. Üs çift sayı ise kuvvet sonucu simetrik bir matristir, ancak üs tek sayı ise kuvvet sonucu antisimetrik bir matristir. Bu bağlantıdan simetrik matrisin ne olduğuna danışabilirsiniz.
- Antisimetrik bir matrisin izi her zaman sıfıra eşittir.
- Herhangi bir antisimetrik matris artı üniter matrisin toplamı, tersinir bir matrise yol açar.
![]()
- Bir antisimetrik matrisin tüm gerçek özdeğerleri (veya özdeğerleri) 0’dır. Bununla birlikte, bir antisimetrik matris aynı zamanda karmaşık özdeğerlere de sahip olabilir.
- Tüm antisimetrik matrisler normal matrislerdir. Bu nedenle antisimetrik bir matrisin üniter bir matris tarafından köşegenleştirilebileceğini söyleyen spektral teoreme tabidirler.
Bir kare matrisin simetrik bir matrise ve bir antisimetrik matrise ayrıştırılması
Kare matrislerin özel bir özelliği, bir simetrik matris artı bir antisimetrik matrisin toplamına ayrıştırılabilmeleridir.
Bunu yapmamızı sağlayan formül şu şekildedir:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b9aa2b7ed0e9ce31587d4f00f1144e_l3.png)
C, ayrıştırmak istediğimiz kare matris olduğunda, C t’nin devriği yapılır ve son olarak S ve A, C matrisinin ayrıştırıldığı sırasıyla simetrik ve antisimetrik matrislerdir.
Aşağıda formülü göstermek için çözülmüş bir alıştırma bulacaksınız. Aşağıdaki matrisi ayrıştıralım:
![Rendered by QuickLaTeX.com \displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5534c773c54b15eab3d0ab4a5823ce6c_l3.png)
Simetrik ve antisimetrik matrisi aşağıdaki formüllerle hesaplıyoruz:
![Rendered by QuickLaTeX.com \displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44ecbf11344f1de645aed313f801fa0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8bc3c78415b6596b99186207efde54e7_l3.png)
Ve iki matrisi toplayarak denklemin yerine getirilip getirilmediğini kontrol edebiliriz:
![]()
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2725b1e3a2de74b4446145ef32b61d1f_l3.png)
![]()
✅