Antihermitian (veya antihermitian) matris

Bu sayfada antihermit matris olarak da adlandırılan antihermit matrisin ne olduğunu göreceksiniz. Anti-Hermitian matrislerin örneklerini, bunların tüm özelliklerini ve bu tür karmaşık kare matrislerin şeklini bulacaksınız. Son olarak, herhangi bir karmaşık matrisin, bir anti-Hermit matrisi artı başka bir Hermit matrisinin toplamına nasıl ayrıştırılacağına ilişkin açıklamayı bulacaksınız.

Antihermitian veya antihermitian matris nedir?

Bir anti-Hermit matrisi veya aynı zamanda anti-Hermit matrisi olarak da adlandırılan, eşlenik devri aynı matrise eşit ancak farklı işaretli karmaşık sayılara sahip bir kare matristir.

$A^*=-A$

Altın

$A^*$

aktarılan eşlenik matrisidir

$A$

Meraktan dolayı, bu tür matrislere, Hermit matrisinin zıt koşulunu yerine getirdiği için bu isim verilmiştir; bu matrisin adı, 19. yüzyılda matematik profesörü ve araştırmacısı olan ve önemli çalışmalar yapan önemli Fransız matematikçi Charles Hermite’den gelmektedir. doğrusal cebir alanı.

Antihermit matris örnekleri

Antihermitian matrisin (veya antihermitian matrisin) tanımını gördükten sonra, farklı boyutlardaki antihermitian matrislerin bazı örneklerini göreceğiz:

2 × 2 mertebesinden bir anti-Hermit matris örneği

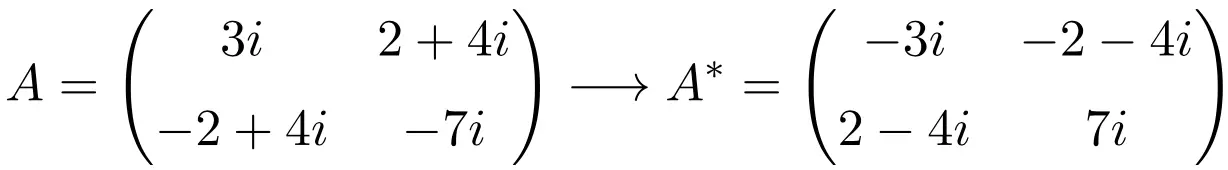
2x2 boyutunda antihermitian veya antihermitian matris

3 × 3 boyutunda bir antihermit matris örneği

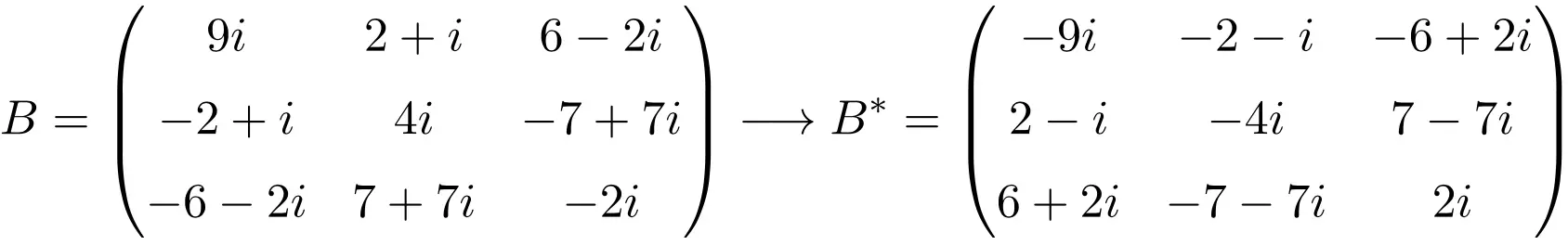
3x3 boyutunda antihermitian veya antihermitian matris

4 × 4 boyutunda bir anti-hermit matris örneği

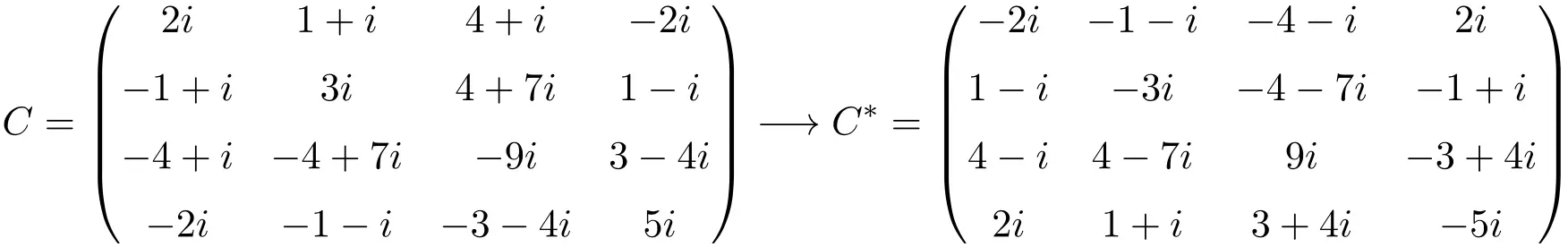
4x4 boyutunda antihermitian veya antihermitian matris

Gördüğünüz gibi, A, B ve C matrisleri anti-Hermitseldir çünkü her birinin eşlenik transpoze matrisi matrisin kendisine eşittir, ancak tüm elemanların işareti değişmiştir.

Bir antihermit matrisinin yapısı

Önceki örneklere daha önce bakmışsanız, Hermit karşıtı matrisler her zaman aynı yapıya sahiptir: ana köşegendeki hayali sayılardan (gerçek kısım olmadan) ve i’inci çizgi ve j’de yer alan karmaşık elemandan oluşurlar. astar. sütun aynı hayali kısma ve aynı gerçek kısma sahip olmalı, ancak j’inci satırın ve i’inci sütunun elemanı olarak işaret değiştirmelidir.

Her ne kadar bu biraz karmaşık görünse de aşağıdaki örnekle kesinlikle daha iyi anlaşılacaktır:

2 × 2 boyutunda bir antihermit matrisinin yapısı

$\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}$

Gördüğünüz gibi, anti-Hermit matrisinin ana köşegeninin elemanları tamamen sanaldır ve ikincil köşegenin elemanları aynı sanal kısma sahiptir ve gerçek kısım işaret değiştirmiştir.

Bu nedenle, bir anti-Hermit matrisinin gerçek kısmı antisimetrik ve sanal kısmı simetrik olmalıdır.

Antihermitian matrisin özellikleri

Şimdi bu tip kare karmaşık matrisin özelliklerinin neler olduğunu göreceğiz:

Her antihermit matrisi normal bir matrisin bir örneğidir . Her ne kadar normal matrislerin tümü antihermitik matrisler olmasa da.

Herhangi bir Hermit karşıtı matris köşegenleştirilebilir. Ayrıca ortaya çıkan diyagonal matris yalnızca tamamen hayali öğeler içerir.

Bu nedenle, Hermit karşıtı bir matrisin özdeğerleri (veya özdeğerleri) her zaman sanal sayılardır.

Benzer şekilde, bir anti-Hermit matrisinin farklı özdeğerlerinin özvektörleri (veya özvektörleri) diktir.

Gerçek sayılardan oluşan bir matris, yani hiçbir elemanın imajiner kısmı olmadığı anlamına gelir, ancak ve ancak antisimetrik bir matris olması durumunda anti-Hermitian’dır.

Bir anti-Hermit matrisi, gerçek bir antisimetrik matris ile hayali bir simetrik matrisin toplamı olarak ifade edilebilir.

$A =B+Ci$

İki Hermit karşıtı matrisin toplamı (veya çıkarılması), başka bir Hermit karşıtı matrise eşittir.

Bir anti-Hermit matrisinin ve bir skalerin çarpımının sonucu, eğer skaler bir gerçek sayı ise, başka bir anti-Hermit matrisidir.

Üs tek ise, Hermit karşıtı bir matrisin gücü, Hermit karşıtı bir matrise eşittir; Öte yandan, eğer çift bir üsse yükseltilirse sonuç bir Hermit matrisi olacaktır.

Evet
$A$

bir antihermit matrisidir, o zaman ürün

$iA$

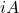
bir Hermit matrisidir.

Karmaşık bir matrisin bir anti-Hermit matrisine ve bir Hermit matrisine ayrıştırılması

Karmaşık sayılar içeren herhangi bir matris , bir anti-Hermit matrisi artı başka bir Hermit matrisinin toplamına ayrıştırılabilir . Ancak bunun için bu tür matrislerin aşağıdaki özelliklerini bilmeniz gerekir:

Bir kare kompleks matris artı bunun transpoze eşleniğinin toplamı bir Hermit (veya Hermit) matrisine eşdeğerdir:

$C + C^* = \text{Matriz Hermitiana}$

Bir kare kompleks matris ile onun transpoze eşleniği arasındaki fark, bir anti-Hermit matrisine eşittir:

$C - C^* = \text{Matriz Antihermitiana}$

Bu nedenle, tüm karmaşık matrisler, bir Hermit matrisi ve bir anti-Hermit matrisinin toplamına ayrıştırılabilir. Bu teorem Teoplitz ayrışımı olarak bilinir:

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

C, ayrıştırmak istediğimiz karmaşık matris olduğunda, C* onun transpoze eşleniğidir ve son olarak A ve B, C matrisinin ayrıştırıldığı sırasıyla Hermit ve anti-Hermit matrisleridir.