Bu fonksiyonu oluşturan farklı değişkenler arasındaki ilişkiyi grafiksel olarak analiz edebilmek için fonksiyonları temsil etmek çok yaygındır. Veya bazen bu tür temsiller birden fazla özelliği satın almak için bile kullanılır. Bu özellikle istatistiksel çalışmalar yürütülürken kullanılır. Bununla birlikte, bugün size herhangi bir fonksiyonun grafiğini çizebilmek için yalnızca 3 adımdan oluşan çok basit bir yöntem açıklayacağız. Ek olarak, sonuçlara varmak için grafiksel sonuçların nasıl analiz edileceğini de tartışacağız.
Fonksiyon türleri
İlk olarak, farklı fonksiyon türlerinin özelliklerini ve bunları temsil ederken hangi farklılıkların dikkate alınması gerektiğini anlamamız gerekir. Bu şekilde grafiksel gösterimi yapmamız daha kolay olacaktır, bu yüzden şimdi her tür hakkında kısaca yorum yapacağız. Pek çok fonksiyon tipinin bulunduğunu belirtmekte fayda var, bu nedenle polinom fonksiyonlarının en önemli iki tipine ve parçalı fonksiyonlara odaklanacağız.
doğrusal fonksiyonlar
Birinci derecenin doğrusal fonksiyonu veya polinom fonksiyonu, ifadesi 1. dereceden bir polinom olan fonksiyondur. Bu durumda, ifadesi f(x) = mx + n modelini takip eder; burada m eğim ve n ordinattır. Temel olarak bu fonksiyonlar çizgiye eşdeğer bir grafik forma sahiptir. Aşağıda bir örnek görebilirsiniz:
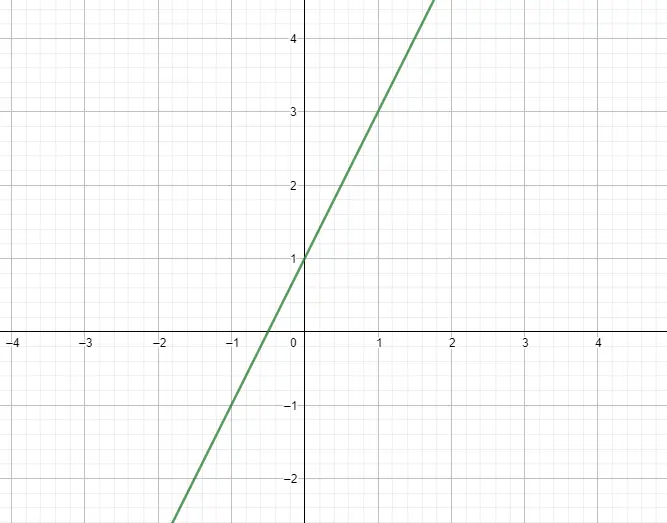
ikinci dereceden fonksiyonlar
İkinci dereceden fonksiyon veya parabolik fonksiyon, ikinci dereceden bir polinom aracılığıyla ifade edilir ve bu nedenle parabolik bir forma sahiptir. İzlenecek model olarak şu ifadeyi dikkate alacağız: f(x) = ax² + bx + c, burada a ≠ 0. Ayrıca bu fonksiyonların iki önemli özelliği daha vardır: genlik ve büyüme. Aşağıda bir örnek görebilirsiniz:
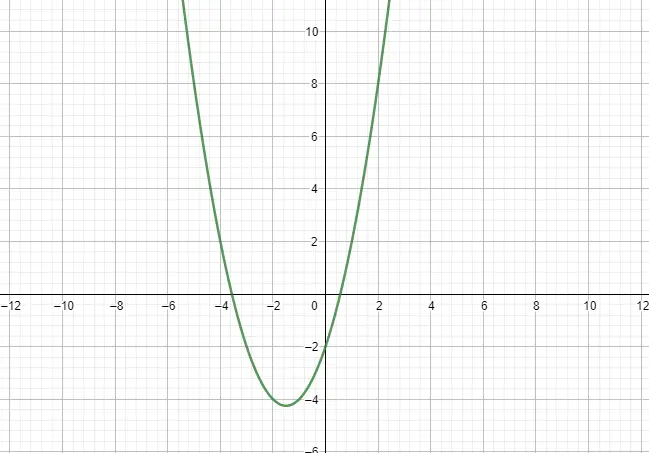
Parçalı fonksiyonlar
Parçalı tanımlı fonksiyon, x değerine bağlı olarak farklı tanımları olan bir fonksiyondur. Dolayısıyla x belirli bir değer aralığını kapladığında bir ifade denememiz gerekir. Oysa x başka değerleri işgal ettiğinde farklı bir ifadenin işlenmesi gerekir. Süreksizlikleri ve dolayısıyla sınırları burada buluyoruz. Çünkü bir işlevin bittiği yerde diğeri başlayabilir, ancak doğrudan bağlanmadan. Aşağıda bir örnek görebilirsiniz:
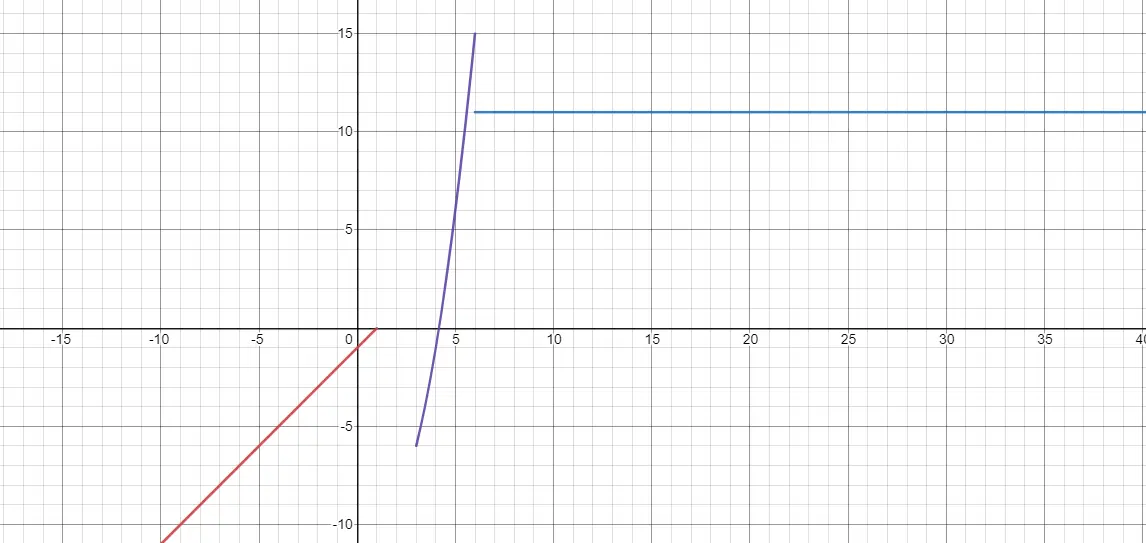
Doğrusal fonksiyonlar nasıl temsil edilir?
Doğrusal bir fonksiyonun grafiğini çizmek için çok basit üç adımı izlememiz gerekir. Daha sonra prosedürü açıklayacağız, ancak parabolik fonksiyonların grafiğinin nasıl çizileceğini öğrenmek istiyorsanız bir sonraki bölüme başvurmanızı öneririz.
Bir değerler tablosu oluşturun
Bir fonksiyonun grafiğini çizebilmek için değişkenlerin tüm değerlerini yazacağımız bir değerler tablosu oluşturmamız gerekiyor. Temel olarak bu, iki değişken arasında bir ilişki kurmamızı sağlayacak ve bu şekilde fonksiyonun yolunu izleyebileceğiz. Eğer değerler tablosu yapmayı bilmiyorsanız bu son bağlantıya bakabilirsiniz. Özet olarak bağımsız değişkene bir değer verilmesi ve bilinmeyenin onunla ilgili fonksiyona yerleştirilmesinden ibarettir. Böylece ilişkili iki sayıya sahip olacağız; aşağıdaki tabloda bir örnek gösterilmektedir:
f(x) = 2x+1 fonksiyonundan:
| X | f(x) |
| 0 | 1 |
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
Grafiğe noktalar çizin ve fonksiyonu çizerek bunları birleştirin
Tabloyu oluşturduktan sonra noktaları grafik üzerinde çizmeye başlayabiliriz. Bunu bağımsız değişkeni x eksenine, diğerini y eksenine ilişkilendirerek yapıyoruz ve bu şekilde puanları elde etmiş oluyoruz. İstediğiniz kadar nokta çizebilirsiniz, ancak bu stildeki işlevleri temsil etmek için genellikle beş noktayı hesaplamak yeterlidir. O günden bu yana düz bir yol izlemişlerdir ve dolayısıyla ne kadar ilerlerseniz ilerleyin, bu aynı şekilde devam edecektir.
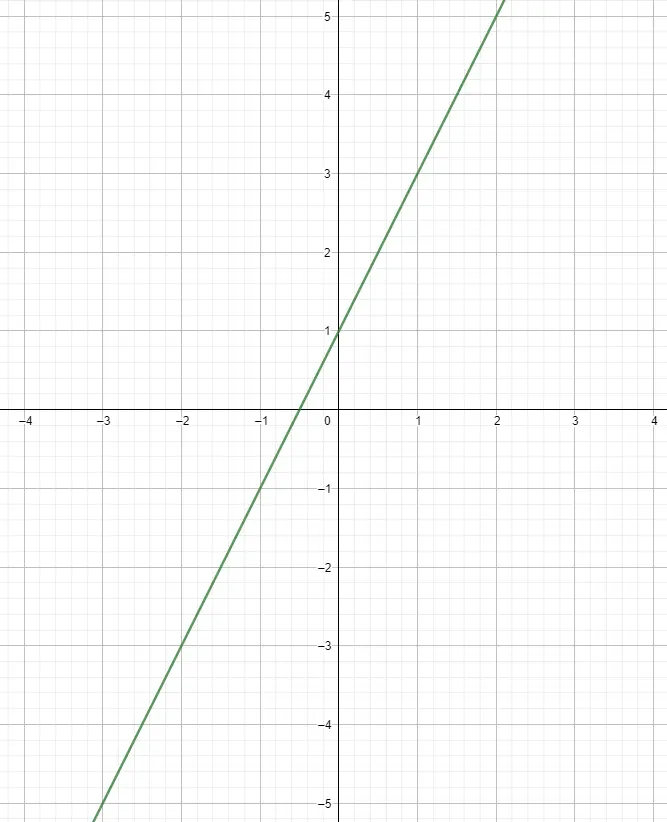
Doğrusal Bir Fonksiyonun Grafiğinin Çizilmesinde Eğimin Kullanılması
Doğrusal fonksiyonları değer tabloları olmadan grafiksel olarak temsil edebilmek için fonksiyonun eğiminin hesaplanmasından oluşan ikinci bir yöntem vardır: m = (dikey değişim / yatay değişim). Yani eğimi hesapladıktan sonra başlangıç noktasına bakmamız gerekiyor. Önceki örneğe dönersek f(x) = 2x+1, başlangıç noktasının (0, 1) olacağını biliyoruz çünkü x = 0’da bilgisayar = 1 (bunu ifadedeki +1’den çıkarıyoruz) . Ve sonra sadece eğimi ekleyin; bu durumda bu, 1 yatay için +2 dikeye eşittir. O zaman bir sonraki noktanın (1,3) olacağını bileceğiz.
İkinci dereceden fonksiyonlar nasıl temsil edilir?
İkinci dereceden bir fonksiyonu temsil etmek için iki yöntemi takip edebiliriz; ilki değer tablolarını içerir. İkincisi ise bir dizi kilit noktanın hesaplanmasından oluşur: tepe noktası, X ekseniyle kesişme noktaları ve Y ekseniyle kesişme noktası. İkincisi aşağıda açıklayacağımız şeydir:
Bir parabolün tepe noktasını hesaplayın
Bir parabolik fonksiyonun tepe noktasını hesaplamamızı sağlayan iki formül vardır, temel olarak biri bize X ekseninin tepe noktasını, diğeri ise Y ekseninin tepe noktasını verir. Her iki formülü de aşağıda bulabilirsiniz ancak her ikisi de benzer yapıya sahiptir.
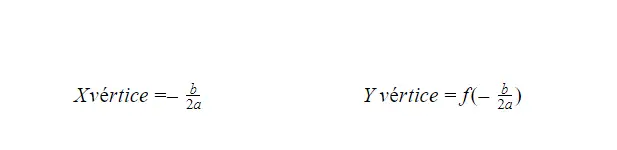
İkinci dereceden bir fonksiyonun X ekseni ile kesişme noktalarını hesaplama
Kesişme noktalarını elde etmek için tek yapmamız gereken denklemi çözmek ve aradığımız X değerlerini zaten elde etmiş olacağız. İkinci dereceden bir fonksiyon olarak sadece bir değil iki sonuç elde edeceğimizi belirtmekte fayda var.
İkinci dereceden bir fonksiyonun Y ekseni ile kesişme noktasını hesaplayın
Son olarak, Y ekseni ile kesişme noktasını elde etmek için c = f(0) değerini hesaplamanız yeterlidir. Ve x = 0 olduğunda bir parabol her zaman dikey eksenle (koordinatlarla) kesiştiği için, Y ekseninin kesme noktasının (0,c) olacağını söyleyeceğiz. Tüm bu noktaları elde ettikten sonra bunları grafik üzerinde çizebiliriz ve parabolü bu şekilde çizerek birleştirmemiz yeterlidir.
Fonksiyonlar parçalı olarak nasıl temsil edilir?
Fonksiyonları parçalar halinde temsil edebilmek için daha önce anlattığımız tüm yöntemleri karıştırabilirsiniz. Çünkü bu tarzdaki fonksiyonlar bahsettiğimiz tüm fonksiyon türlerinden oluşmaktadır. Bu nedenle, bazılarını bir değerler tablosu aracılığıyla hesaplamanız gerekecek, bazılarını ise başka yöntemlerle hesaplamanız gerekecek. Ancak bu yazımızda anlattıklarımıza hakim olduğunuzda artık fonksiyonları parçalı olarak temsil etmekte sorun yaşamazsınız.
Öte yandan, bunları temsil ederken bir süreklilik çalışması yapmanız gerektiğinden, henüz bilmiyorsanız, sınırları nasıl çözeceğinizi öğrenmenizi öneririz. Bu, her işlevin uç noktalarını doğru şekilde temsil etmenize yardımcı olacaktır. Bununla birlikte, artık parçalı fonksiyonların ve diğer fonksiyon türlerinin grafiğini çizmeye hazır olacaksınız. Şimdi sizi bir dizi grafik ipucuyla ve hesap makinesinin grafik oluşturma becerisine ilişkin çok yararlı bir açıklamayla baş başa bırakıyoruz.
Hesap makinesiyle grafikler nasıl yapılır?
Bir grafik hesap makineniz varsa, grafik oluşturma yeteneğine sahip olacaktır. Prosedürü öğrendikten sonra bunu yapmak çok kolay olabilir, ancak hala nasıl yapacağınızı bilmiyorsanız, şimdi size açıklayacağız.
- Grafik moduna erişim: İlk adım, menüden grafikler veya grafik gösterimler seçeneğine erişmektir. Bu seçenek hesap makineniz için farklı bir adla etiketlenmiş olabilir, ancak grafik çizmeye benzer veya daha önce bahsettiğimiz sözcükleri içerecektir.
- Grafik seçeneklerini özelleştirin: Grafik düzenleyiciye girdikten sonra dosyaya bir ad vermeli, eksenleri etiketlemeli, grafiği oluşturulacak öğe sayısını seçmeli ve gösterimin estetik seçeneklerini yapılandırmalıyız. Bu çok hızlı bir adımdır.
- Fonksiyonun noktalarını ekleyin: Daha sonra şekli oluşturacak noktaları eklemeye başlayabilirsiniz. Bunu, noktaları aşağıdaki notasyonla yazarak yapabilirsiniz: (0,1), (3,2)… Ve grafiği bitirinceye kadar noktaları eklemeye devam edeceksiniz.
- “Önizleme” işlevini kullanın: Projeyi bitirdikten sonra sonucu önizleyebilir ve beklendiği gibi çıkıp çıkmadığını görebilirsiniz. Ayrıca birçok şablonun bu önizlemede düzenleme seçenekleri vardır, böylece sonucu mükemmel olana kadar değiştirebilirsiniz.
- Projeyi kaydedin: Tüm düzenleme prosedürü tamamlandıktan sonra, onu hatırlanması kolay bir konuma kaydetmeyi unutmayın. Bu sayede ihtiyaç duyduğunuz anda projeye tekrar ulaşarak projeyi görüntüleyebilir veya istediğiniz iyileştirmeleri yapabilirsiniz.
İşlevleri temsil etmek için en iyi hesap makineleri
Aynı hesap makinesindeki işlevleri temsil edebilecek bir grafik modeli satın almakla ilgileniyorsanız iki model öneririz: HP 50G ve HP Prime . Bunlar pahalı olmalarına rağmen en kaliteli modellerden ikisidir, bu nedenle yatırımın sizin için değip değmeyeceğini kendinize sormanız gerekir. Örneğin mühendislik gibi matematik açısından oldukça karmaşık bir kariyer okuyacaksanız bu iki modelden birini satın almanız şiddetle tavsiye edilecektir. Ancak çok fazla bilgi işlem veya grafik gücüne ihtiyacınız yoksa belki Casio FX-9750GII sizin için yeterli olacaktır.
Fonksiyonların çevrimiçi grafiği nasıl çizilir?
Her zaman çevrimiçi grafik programlarını kullanma seçeneğini seçebilirsiniz, örneğin: Desmos , Geogebra ve diğerleri. Bu şekilde hızlı bir şekilde çok doğru grafikler elde edeceksiniz. Fonksiyonların grafiklerini kolay ve hızlı bir şekilde çizmek istediğinizde sayı formunun kullanıldığını söyleyebiliriz. Öte yandan, fonksiyonları düzenleyebilmeniz (tüm niteliklerini değiştirebilmeniz) ve yüksek kaliteli fonksiyon analizi kaynaklarının parmaklarınızın ucunda olması için grafiklerini oluşturmak istiyorsanız, o zaman bir bilimsel hesap makinesi satın almanızı öneririz.