Ruffini kuralı, Paolo Ruffini tarafından geliştirilen ve (x – a) formundaki polinomları bölmemize izin veren matematiksel bir prosedürdür . Bu matematiksel yöntem aynı zamanda sentetik bölme olarak da bilinir. Peki bu prosedür nasıl kullanılır ve adımları nelerdir? Ve bir Ruffini egzersizini hesap makinesiyle nasıl çözebilirim? Tüm bunları bu yazımızda sizlere özetlenmiş ve anlaşılması kolay bir şekilde anlatacağız, ayrıca Ruffini için en iyi hesap makinelerini önereceğiz.
Ruffini hesaplayıcı çevrimiçi
Bir polinomu çarpanlara ayırmak istiyorsanız, aşağıdaki sembolleri kullanarak yazdığınız sürece herhangi bir ifadeyi çarpanlara ayırmanıza olanak tanıyan bu hesap makinesini kullanabilirsiniz: ^ (yükselt) ve / (böl). Ve içiniz rahat olsun, çünkü bu hesap makinesi 3. derece ve hatta daha yüksek dereceli polinomları çarpanlarına ayırma yeteneğine sahiptir. Bu nedenle çevrimiçi polinomları çarpanlara ayırmak için en iyi hesaplama aracıdır.
Ruffini nasıl uygulanır?
Bu bölümde Ruffini’nin nasıl gerçekleştirileceğini açıklayacağız ve yöntemi kullanarak belirli bir örneği çözeceğiz, böylece tüm prosedürü net ve grafiksel olarak görebileceksiniz. Bu da bu kavramı kökünden anlamanızı sağlayacak ve daha sonra sınavda hatırlayacaksınız. Ayrıca yazılı anlatımla ilgili tereddütleriniz olsa bile bu kavramı anlamanızı sağlayacak açıklayıcı bir videoya da yer verdik.
Ruffini yöntemini kullanmak için gerekenler
Polinomların bir bölümünü çözmeye başlamadan veya bir polinomu çarpanlarına ayırmadan önce bölene bakmanız gerekir. Birinci derece ise Ruffini yöntemine geçebiliriz. Öte yandan bölenin derecesi 1’den büyükse bu işlemi uygulayarak hesaplamayı çözemeyiz. Bu nedenle polinomları bölmek için başka bir yöntem kullanmak zorundayız. Bu, hesaplamalara başlamadan önce kontrol edilmesi gereken bir faktördür, aksi takdirde çok fazla zaman kaybedebilirsiniz.
Ruffini kuralını kullanarak polinomları bölme prosedürü
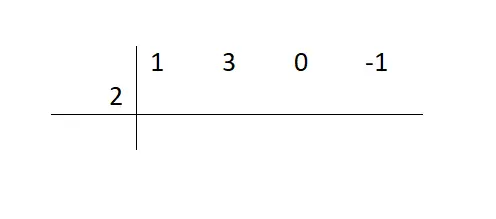
Artık bu matematiksel kaynağın ne zaman kullanılabileceğini bildiğimize göre, bir polinomu çarpanlara ayırabilmek için izlenecek farklı adımları göreceğiz. Dolayısıyla, (x³+3x²-1) / (x-2) örneğinden yola çıkarak, öncelikle bölünme katsayılarını, eksik terimleri sıfırla temsil eden yatay bir çizgiye yazmalıyız . Daha sonra bölenin bağımsız terimini resimde gösterildiği gibi ayrı zıt işarete koyacağız.
Daha sonra, ilk katsayıyı (daha yüksek bir üsse yükselen değişkene eşlik eden katsayı) düşürmeliyiz . Bu sayıyı azaltıp bir sonraki adıma geçeceğimiz için herhangi bir şey yapmayacağız.
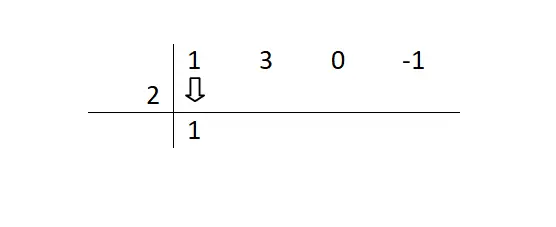
Daha sonra, oldukça tekrarlayan bir dizi adımla başlayacağız: düşürdüğümüz sayıyı bölenle çarpacağız ve sonucu bir sonraki terime koyacağız. Daha sonra bu sonucun arasına bir sonraki terimi ekleyip ilk yazdığımız sayının yanına yazacağız.
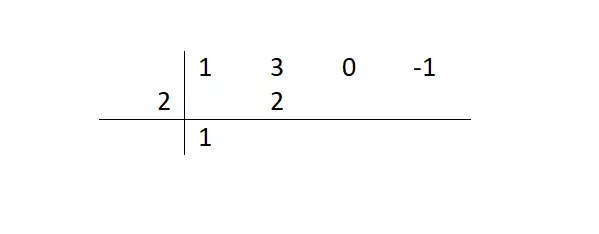
Tabloyu tamamlayana kadar bu adımları takip edersek aşağıdaki düzene sahip oluruz. Böylece kalanın 19’a eşit olduğunu (son hesapladığımız sayı) ve kalan ifadesinin (bölüm) x²+5x+10 olacağını bileceğiz. Tüm bu bilgileri alt satırdaki rakamlardan aldık. Ve bir polinomun çarpanlarına ayrılması durumunda, diğer kökleri bulmaya devam etmek için bu bölümü kullanmalıyız.
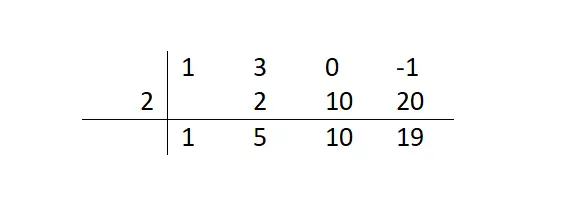
Ruffini’yi hesap makinesine nasıl koyabilirim?
Hesap makinesinde polinomları Ruffini ile bölebilmek için hesap makinesinin çözücülerine, yani denklem hesaplama moduna erişmeniz yeterlidir. İçeri girdikten sonra polinom denklemleri seçeneğini seçeceğiz çünkü bir polinomu çarpanlara ayırmak istiyoruz. Daha sonra ifadenin derecesini seçeceğiz ve matematik editörüne girebileceğiz, dolayısıyla ifadeyi tanıtacağız. Yani polinomun köklerini bulduğumuzda, onu yalnızca (x – a) biçiminde yazmamız gerekecek. Bu prosedürün tamamı (kök kısım hariç), denklemleri hesap makinesiyle çözmek için kullanacağımız prosedürle aynıdır.
Ruffini teoremini hesaplamak için en iyi hesap makineleri
Şu anda polinomlarla işlemleri çözebilen ve bunları çarpanlarına ayırabilen birçok hesap makinesi bulabiliriz. Ancak kullanım kolaylığı ve fiyat açısından öne çıkan bazı modeller var. Bunun iki güzel örneği Casio FX-991SPX II ve Casio FX-991ES PLUS’tur , aslında bir önceki bölümde yaptığımız açıklama bu iki modelin işleyişini temel alıyor. Bununla birlikte, daha önce de söylediğimiz gibi, Ruffini’yi mükemmel bir şekilde yapmanıza yardımcı olacak başka bilimsel hesap makineleri de bulabilirsiniz.
Ruffini Örnekleri ve Alıştırmaları
Ruffini kuralı, başlangıçta yorumladığımız kurallara uydukları sürece iki polinomun rastgele alınmasıyla uygulanabilir. Bununla birlikte, bu matematiksel prosedür aracılığıyla birden büyük dereceli polinomları çarpanlara ayırmayı da deneyebilirsiniz. Böylece aynı matematiksel mekanizmayı inceleyecek ve ardından bir polinomun kökü kavramını gözden geçireceksiniz. Daha sonra, çarpanlarına ayırmanız gereken iki polinomu ve Ruffini yöntemini kullanarak çözmeniz gereken oldukça basit bir bölme işlemini göstereceğiz.
1. Egzersiz
Polinomu çarpanlara ayırın: 2x³-7x²+8x-3
Kökler: x=1 ve x=1, dolayısıyla elimizde (x-1)²(2x-3) kalır
Alıştırma 2
Polinomu çarpanlara ayırın: x³+2x²-x-2
Kökler: x=-2, x=-1 ve x=1, yani elimizde (x+2)(x+1)(x-1) kalır
Alıştırma 3
Polinomlar arasındaki aşağıdaki bölmeyi çözün: (3x³-5x²+2) / (x-2)
Bölüm: 3x²+x+2, kalan: 6
Daha fazla Ruffini egzersizi istiyorsanız, bu makaledeki prosedürlerin aynısını açıklayan bu Superprof makalesini izlemenizi öneririz. Ancak Ruffini’den biraz farklı örnekler ve alıştırmalarla, daha fazla pratik yaparak bazı şüphelerinizi giderebilirsiniz. Her iki durumda da içeriğimizi ve Ruffini Hesaplayıcıyı faydalı bulduğunuzu umuyoruz.