▷ 3 (veya daha fazla) noktanın hizalı olup olmadığını nasıl anlarım? ✅

Bu sayfada hizalanmış noktaların ne olduğuna dair açıklama bulacaksınız. Ayrıca 3 (veya daha fazla) noktanın hizalanıp hizalanmadığını belirlemek için mevcut tüm yöntemleri göreceksiniz. Dahası, pratik yapabilmeniz için çeşitli örnekler ve hatta çözülmüş alıştırmalar bulacaksınız.

Noktaların hizalanması ne anlama geliyor?

Analitik geometride üç veya daha fazla nokta, hepsi aynı çizgi üzerindeyse, yani aralarına düz bir çizgi çizilerek birleştirilebiliyorsa hizalanır .

Açıkçası, iki nokta arasına her zaman bir çizgi çizebildiğiniz için 2 nokta her zaman hizalanacaktır. Ancak üç noktanın aynı doğru üzerinde olması şart değildir. Temel olarak 3 veya daha fazla noktanın hizalanıp hizalanmadığını anlamanın iki yöntemi vardır:

Vektör yöntemi : Noktaları oluşturan vektörlerin orantılı olup olmadığına bakmaktan oluşur.
Doğru denklemi yöntemi : Noktaların aynı doğruya ait olup olmadığının belirlenmesinden oluşur.

Aşağıda her bir prosedürün açıklaması ve örnekleri verilmiştir; böylece hangisinin sizin için en iyi olduğuna karar verebilirsiniz.

3 (veya daha fazla) noktanın vektör yöntemiyle hizalanıp hizalanmadığı nasıl anlaşılır?

Üç nokta göz önüne alındığında:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Vektörler eğer üç nokta hizalanırsa

$\vv{AB}$

$\vv{BC}$

aynı yöne sahiptirler, yani bileşenleri orantılıdır.

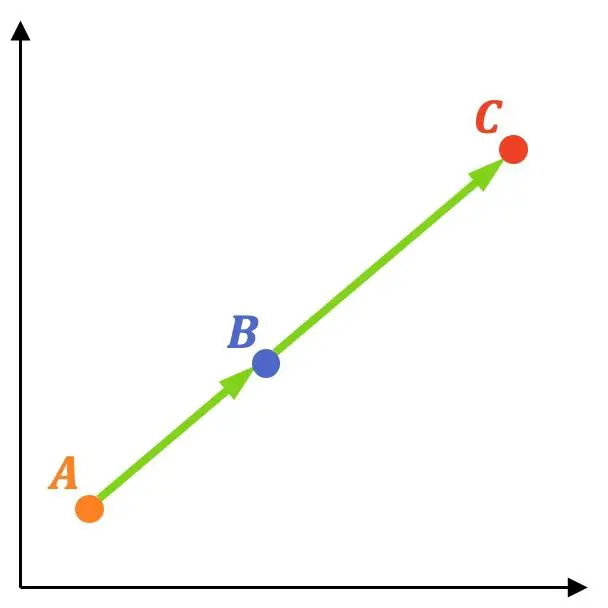
Bunun nasıl yapıldığına dair bir örnek görelim:

Aşağıdaki 3 noktanın hizalı olup olmadığını belirleyin:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Öncelikle noktalar arasındaki vektörleri hesaplıyoruz. İki farklı vektörü hesaplamak yeterlidir:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

Daha sonra vektörlerin koordinatlarının orantılı olup olmadığını kontrol ederiz:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

İki vektörün X bileşenlerini ve Y bileşenlerini bölerek aynı sonucu (-2) elde ederiz, dolayısıyla vektörler aynı yöne sahiptir ve dolayısıyla noktalar hizalıdır .

Bu yöntem aynı zamanda uzayda (R3’te) üç veya daha fazla noktanın hizalı olup olmadığını bulmak için de kullanılabilir, eklenmesi gereken tek şey, iki vektörün üçüncü bileşeninin (Z bileşeni) de orantılı olup olmadığını kontrol etmektir.

Bu makale sizin için yararlıysa, muhtemelen iki nokta arasındaki orta noktanın nasıl hesaplanacağını bilmek de ilginizi çekecektir, çünkü açıkçası, 2 noktanın orta noktasını bulmak, diğer iki noktayla hizalanmış üçüncü bir noktayı belirlemenin bir yoludur. Bağlantılı sayfada bunun nasıl yapıldığını görebilir, ayrıca adım adım çözülmüş örnekleri ve alıştırmaları da görebileceksiniz.

Düz çizgi denklemi yöntemiyle 3 (veya daha fazla) noktanın hizalı olup olmadığı nasıl anlaşılır?

Önceki bölümde gördüğümüz gibi, 3 veya daha fazla noktanın hizalamasını incelemenin bir yolu, aralarında oluşabilecek vektörleri kullanmaktır. Başka bir yöntem ise bir doğrunun denklemiyle başlamaktır:

Üç nokta göz önüne alındığında:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Üç noktanın tümü aynı çizgiye aitse hizalanır. Bu nedenle üç veya daha fazla noktanın hizalı olup olmadığını bilmek için aşağıdaki adımlar izlenmelidir:

Üç noktadan ikisinden geçen doğrunun denklemini bulun.
Üçüncü noktanın da doğruya ait olup olmadığını kontrol edin. Bu durumda 3 noktanın hizalı olduğu, ancak koşulun karşılanmaması durumunda noktaların hizalı olmadığı anlamına gelir.

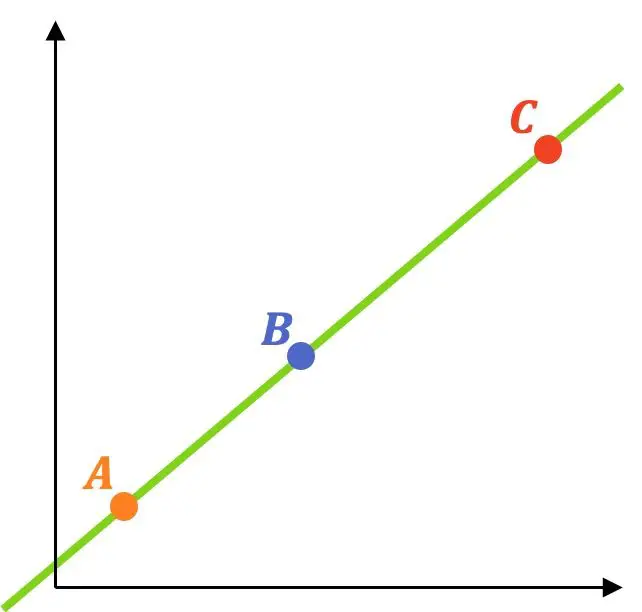
Örnek olarak, bu yöntemi kullanarak bir alıştırmayı çözeceğiz:

Aşağıdaki 3 noktanın hizalı olup olmadığını kontrol edin:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Öncelikle A ve B noktalarından geçen doğrunun denklemini hesaplamamız gerekiyor. Böylece doğrunun yön vektörünü buluyoruz:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Şimdi doğrunun denklemini oluşturmanız gerekiyor, istediğiniz türü seçebilirsiniz: parametrik, örtülü, genel vb. Ancak bu durumda sürekli denklemi kullanacağız. A noktasından ve B noktasından geçen doğrunun sürekli denklemi şöyle olacaktır:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Doğrunun denklemini bulduktan sonra diğer noktanın da aynı doğruya ait olup olmadığını kontrol etmeliyiz. Bunu yapmak için C noktasının koordinatlarını çizginin denkleminde yerine koyarız:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

Beraberlik elde ettik, yani nokta doğrunun denklemini karşılıyor. Ve bu nedenle 3 nokta doğrusaldır .

Bir dizi hizalı noktanın eşit uzaklıkta olması gerekmediği, yani birkaç hizalı nokta arasındaki mesafenin farklı olabileceği dikkate alınmalıdır. İki nokta arasındaki mesafenin (geometri) açıklamasında iki kavram arasındaki farkı görebilir, ayrıca adım adım çözülmüş örnekleri ve alıştırmaları da görebilirsiniz.

Çözülmüş hizalanmış noktalar egzersizleri

1. Egzersiz

Aşağıdaki 3 noktanın hizalı olup olmadığını belirleyin:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Çözümü görün

Sorunun çözümü için gördüğümüz iki yöntemden birini seçebiliriz. Bu durumda vektör yöntemini kullanacağız.

İlk önce noktalar arasındaki vektörleri hesaplıyoruz:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

Şimdi vektörlerin Kartezyen koordinatlarının orantılı olup olmadığını kontrol ediyoruz:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

İki vektörün X bileşenlerini ve Y bileşenlerini birbirine bölerek aynı sonucu (-4) elde ederiz, dolayısıyla vektörler aynı yöne sahiptir. Noktaların hizalandığını gösteren olgu.

Alıştırma 2

3 puan verildi:

$A(6,3) \quad B(4,-3) \quad C(4,5)$

Hangilerinin aşağıdaki iki noktayla aynı hizada olduğunu belirleyin:

$D(3,-1) \quad E(2,1)$

Çözümü görün

Bu durumda düz çizgi denklemi yöntemini kullanacağız, böylece bazı hesaplamaları kaydedeceğiz.

Bu nedenle D ve E noktalarından geçen doğrunun sürekli denklemini hesaplıyoruz:

$\vv{DE} = E-D = (2,1) - (3,-1) = (-1,2)$

$\cfrac{x-3}{-1}=\cfrac{y+1}{2}$

Şimdi hangi noktaların çizginin denklemine karşılık geldiğini ve dolayısıyla D ve E noktalarıyla hizalandığını ve hangilerinin olmadığını kontrol edelim.

A noktasını kontrol ediyoruz:

$\cfrac{6-3}{-1}=\cfrac{3+1}{2}$