Bu sayfada vektörler arasındaki doğrusal kombinasyonun ne anlama geldiğinin açıklamasını bulacaksınız. Ayrıca bir vektörün doğrusal kombinasyon olarak nasıl ifade edildiğine dair bir örnek görebileceksiniz ve ayrıca adım adım çözülen alıştırmalar ve problemlerle pratik yapabileceksiniz.
Vektörlerin doğrusal birleşimi nedir?
Doğrusal kombinasyonun tanımı aşağıdaki gibidir:
Bir vektör kümesinin doğrusal birleşimi, kümedeki tüm vektörlerin skalerlerle (gerçek sayılar) çarpılmasıyla elde edilen vektördür.
Başka bir deyişle, bir dizi vektör verildiğinde
![]()
bunların doğrusal bir kombinasyonu şöyle olacaktır:
![]()
Katsayılar nerede
![]()
Bunlar gerçek sayılardır.
Bu nedenle, diğer vektörlerin doğrusal birleşimi olan bir vektör, birincisinin ikinci cinsinden ifade edilebileceği anlamına gelir.
Bu kavram, iki vektörün doğrusal birleşimi olan bir vektörün düzlemde grafiği çizilerek daha iyi anlaşılabilir:
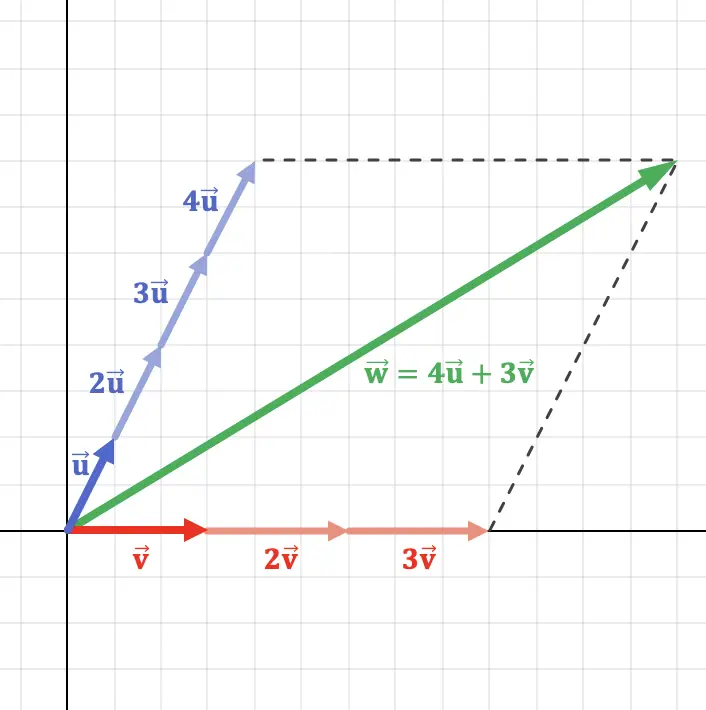
Yukarıdaki grafiksel gösterimde görebileceğiniz gibi, vektör
![]()
vektörlerden elde edilebilir
![]()
Ve
![]()
Vektör işlemlerini gerçekleştirin. Bu nedenle vektör
![]()
diğer iki vektörün doğrusal birleşimidir.
Bu doğrusal kombinasyonun benzersiz olduğunu, başka bir deyişle her vektör için yalnızca bir tane uygulanabilir doğrusal kombinasyonun bulunduğunu vurgulamak gerekir. Önceki örneği takip ederek çarparsak
![]()
4 yerine 6 için başka bir farklı vektör elde ederiz.
Ayrıca, düzlemdeki (R2’deki) doğrusal kombinasyonun özelliklerinden biri, herhangi bir vektörün, eğer farklı yönlere sahiplerse, yani paralel değillerse, diğer iki vektörün doğrusal birleşimi olarak yerleştirilebilmesidir.
Ayrıca bazen iki vektörün doğrusal bir kombinasyon olduğunu gözle tespit edebiliriz. Bunu yapmak için bileşenlerinin orantılı olması yeterlidir. Örneğin, aşağıdaki iki vektörün koordinatları orantılıdır ve dolayısıyla vektörler doğrusal bir kombinasyondur:
![]()
![Rendered by QuickLaTeX.com \cfrac{3}{1} = \cfrac{6}{2} = \cfrac{-3}{-1} = 3 \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac41542948764e158ebe590c6b36e67_l3.png)
Son olarak, ister iki boyutlu (R2’de) ister üç boyutlu (R3’te) vektör uzayında, eğer bir vektör kümesi içinde doğrusal bir kombinasyon varsa, bu onların birbirlerine doğrusal olarak bağımlı oldukları anlamına gelir. Öte yandan, vektörler arasında doğrusal bir kombinasyon mümkün değilse bu onların doğrusal olarak bağımsız olduğu anlamına gelir.
Bu son kavram sizin için tamamen açık değilse, doğrusal olarak bağımlı ve bağımsız vektörlere ilişkin açıklamamıza göz atmanızı öneririz; burada vektörlerin doğrusal olarak bağımlı veya bağımsız olmasının ne anlama geldiğini, her türün örneklerini ve aralarındaki farkları bulacaksınız. . Bu kavram çok kullanılıyor ve aslında sınavlarda da çok soruluyor, bu yüzden onu iyi anlamanız önemli.
Bir vektör diğer vektörlerin doğrusal birleşimi olarak nasıl ifade edilir?
Daha sonra bir vektörün doğrusal birleşimini bulmamızın istendiği tipik bir problemi nasıl çözeceğimizi göreceğiz.
- Vektörü ifade edin
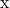
doğrusal bir kombinasyonu olarak
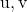
Ve
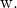
![]()
![]()
Böylece vektör
![]()
diğer vektörlerin doğrusal birleşimi olması için aşağıdaki denklemin yerine getirilmesi gerekir:
![]()
Katsayılar nerede
![]()
Ve
![]()
Bunlar bulmamız gereken bilinmeyenler.
Bu nedenle her vektörü koordinatlarıyla değiştiririz:
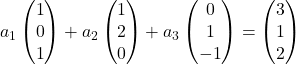
Her vektörü katsayısıyla çarpıyoruz:
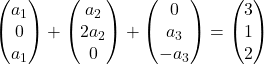
Vektörleri ekliyoruz:
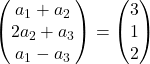
Her sol koordinat her sağ koordinata eşit olmalıdır. Bu nedenle 3 denklemimiz var:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] a_1-a_3 = 2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8e5fe050102a285a325dcd81d07ef5d5_l3.png)
Geriye kalan tek şey elde edilen denklem sistemini çözmektir. Bunu yapmak için tercih ettiğiniz yöntemi kullanın (ikame yöntemi, Cramer kuralı, Gauss-Jordan yöntemi vb.), bu durumda Gauss yöntemini kullanacağız:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8aa4e245614f286e0697797a18ba4465_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 1&0&-1&2 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f1d9c941fe239bb40297b998eb6929_l3.png)
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&-1&-1&-1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2F_3+F_2}\end{array} \left( \begin{array}{ccc|c} 1&1&0& 3 \\[2ex] 0&2&1&1\\[2ex] 0&0&-1&-1 \end{array}\right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-02a8a00406479f367627b682099e05c0_l3.png)
Dolayısıyla elde edilen adımların sistemi şu şekildedir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2 = 3 \\[2ex] 2a_2+a_3 =1\\[2ex] -a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-74ed1b18779582d6683ecaa1a9085e3d_l3.png)
Artık yapmamız gereken tek şey bilinmeyenleri açıklığa kavuşturmak ve değerini bulmak. Yani bulduğumuz son denklemden
![]()
![]()
Sistemin ikinci denkleminden değerini hesaplıyoruz.
![]()
![]()
![]()
![]()
![]()
Ve son olarak, adımlar sisteminin ilk denkleminden bilinmeyeni buluyoruz
![]()
![]()
Dolayısıyla doğrusal denklem sisteminin çözümü şu şekildedir:
![]()
Yani vektör
![]()
Aşağıdaki doğrusal kombinasyonla ifade edilebilir:
![]()
![]()
![]()
Bu nedenle vektörler arasında etkin bir doğrusal bağımlılık vardır. Öte yandan, denklem sisteminin hiçbir çözümü elde edilmemiş olsaydı, bu, vektörün şu anlama geleceği anlamına gelirdi:
![]()
Diğer vektörlere göre doğrusal olarak bağımsızdır ve dolayısıyla söz konusu vektörü diğer vektörlerden elde etmek için olası bir doğrusal kombinasyon olmayacaktır.
Vektörlerin doğrusal kombinasyonuna ilişkin çözülmüş alıştırmalar
1. Egzersiz
Aşağıdaki üç vektör arasında hangi çiftlerin birbirinin doğrusal birleşimi olduğunu belirtin. Ek olarak söz konusu vektör çiftlerinin doğrusal kombinasyon ilişkisini bulun.
![]()
Bir vektör çiftinin doğrusal bir kombinasyon olup olmadığını bilmek için koordinatlarının orantılı olup olmadığına bakmalıyız.
İlk önce vektörü kontrol ediyoruz
![]()
vektör ile
![]()
![]()
İkinci olarak vektörü kontrol ediyoruz
![]()
vektör ile
![]()
![]()
Son olarak vektörü test ediyoruz
![]()
vektör ile
![]()
![Rendered by QuickLaTeX.com \cfrac{1}{-3} = \cfrac{2}{-6} = \cfrac{-3}{9} = -\cfrac{1}{3} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \begin{array}{c} \text{Combinaci\'on}\\[2ex] \text{lineal} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f818eb5ae0825dd43290331519599c21_l3.png)
Yani doğrusal kombinasyon olan tek vektör çifti
![]()
Ve
![]()
Ayrıca aralarındaki ilişki şu şekildedir:
![]()
Veya eşdeğer:
![]()
İfade bunu gerektirmese de, birbirine doğrusal olarak bağlı olan tek vektörler
![]()
Ve
![]()
çünkü aralarında doğrusal bir kombinasyon var. Diğer çiftler doğrusal olarak birleştirilemedikleri için doğrusal olarak bağımsızdırlar.
Alıştırma 2
Vektör arasındaki doğrusal ilişkiyi bulun
![]()
ve vektörler kümesi
![]()
Ve
![]()
![]()
![]()
Böylece vektör
![]()
diğer vektörlerin doğrusal birleşimi olması için aşağıdaki denklemin yerine getirilmesi gerekir:
![]()
Bu nedenle her vektörü koordinatlarıyla değiştiririz:
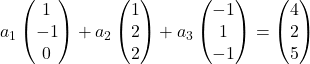
Her vektörü sabitiyle çarpıyoruz:
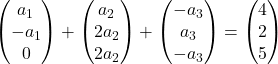
Vektörleri ekliyoruz:
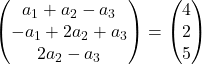
Bu nedenle aşağıdaki denklem sistemini elde ederiz:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +a_2-a_3 = 4 \\[2ex] -a_1+2a_2+a_3 =2\\[2ex] 2a_2-a_3 = 5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ea3ca998fc7d9d9b2cf42d43a5bf0a4_l3.png)
Gauss yöntemiyle elde edilen sistemi çözüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c808441bc71bd26e333ebe2169b738ca_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] -1&2&1&2\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2+F_1}\\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-941792a2de155bc284b14e34dc561418_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&2&-1&5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3F_3-2F_2} \end{array} \left( \begin{array}{ccc|c} 1&1&-1& 4 \\[2ex] 0&3&0&6\\[2ex] 0&0&-3&3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7105de2fa579f40818bccc2df48961ab_l3.png)
Dolayısıyla elde edilen adımların sistemi şu şekildedir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +a_2-a_3 = 4 \\[2ex] 3a_2 =6\\[2ex] -3a_3 = 3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd5b2d564f66cd225c1a5987241ba14_l3.png)
Artık yapmamız gereken tek şey bilinmeyenleri açıklığa kavuşturmak ve değerini bulmak. Yani bulduğumuz son denklemden
![]()
![]()
![]()
Sistemin ikinci denkleminden değerini hesaplıyoruz.
![]()
![]()
![]()
Ve son olarak, adımlar sisteminin ilk denkleminden bilinmeyeni buluyoruz
![]()
![]()
![]()
![]()
Dolayısıyla doğrusal denklem sisteminin çözümü şu şekildedir:
![]()
Yani vektör
![]()
Aşağıdaki doğrusal kombinasyonla ifade edilebilir:
![]()
![]()
![]()
Alıştırma 3
Vektörü ifade edin
![]()
vektörlerin doğrusal birleşimi olarak
![]()
Ve
![]()
![]()
![]()
Vektöre göre doğrusal kombinasyon denklemini öneriyoruz
![]()
![]()
Bu nedenle her vektörü kendi bileşenleriyle değiştiriyoruz:
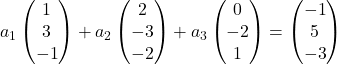
Her vektörü kendi bilinmeyeniyle çarpıyoruz:
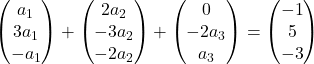
Vektörlerin eklenmesini gerçekleştiriyoruz:
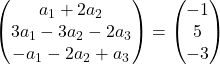
Bu nedenle aşağıdaki denklem sistemini elde ettik:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1 +2a_2 = -1 \\[2ex] 3a_1-3a_2-2a_3 =5\\[2ex] -a_1-2a_2+a_3 = -3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-acdcf13a945bca16684be340d27e3523_l3.png)
Gauss yöntemiyle elde edilen sistemi çözüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e49ae26fc68a865214bd9b6146b7aa99_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 3&-3&-2&5\\[2ex] -1&-2&1&-3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{F_2-3F_1}\\[2ex] \xrightarrow{F_3+F_1} \end{array} \left( \begin{array}{ccc|c} 1&2&0& -1 \\[2ex] 0&-9&-2&8\\[2ex] 0&0&1&-4\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4c56b420242d0abe6f77b3ed1a60e54_l3.png)
Dolayısıyla elde edilen adımların sistemi şu şekildedir:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1 +2a_2 = -1 \\[2ex] -9a_2-2a_3 =8\\[2ex] a_3 = -4 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-03461ed9ebda463d2f0a1bb6894657be_l3.png)
Artık yapmamız gereken tek şey bilinmeyenleri açıklığa kavuşturmak ve değerini bulmak. Yani bulduğumuz son denklemden
![]()
![]()
Sistemin ikinci denkleminden değerini buluyoruz.
![]()
![]()
![]()
![]()
![]()
![]()
Ve son olarak, adımlar sisteminin ilk denkleminden bilinmeyeni çözüyoruz
![]()
![]()
Dolayısıyla doğrusal denklem sisteminin çözümü şu şekildedir:
![]()
Yani vektör
![]()
diğer vektörlerin doğrusal olarak birleştirilmesiyle ifade edilebilir:
![]()
![]()
![]()
Alıştırma 4
Vektörün olup olmadığını belirleyin
![]()
vektörlerden doğrusal bir kombinasyon olarak ifade edilebilir
![]()
Ve
![]()
Bu durumda onları birbirine bağlayan ifadeyi bulun.
![]()
![]()
Böylece vektör
![]()
diğer vektörlerin doğrusal birleşimi olması için aşağıdaki denklemin yerine getirilmesi gerekir:
![]()
Bu nedenle her vektörü koordinatlarıyla değiştiririz:
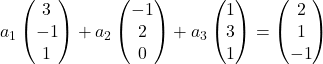
Her vektörü katsayısıyla çarpıyoruz:
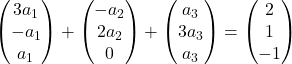
Vektörleri ekliyoruz:
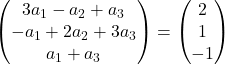
Bu nedenle önceki ifade aşağıdaki denklem sistemine eşdeğerdir:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} 3a_1 -a_2+a_3 = 2 \\[2ex] -a_1+2a_2+3a_3 =1\\[2ex] a_1+a_3 = -1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f51b7e801b8314c51b983f1f24be15e4_l3.png)
Şimdi Gauss yöntemiyle elde edilen sistemi çözüyoruz:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-031b14d5aca6a41d897ca575440b1197_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] -1&2&3&1\\[2ex] 1&0&1&-1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{3F_2+F_1}\\[2ex] \xrightarrow{3F_3-F_1} \end{array} \left( \begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2caf1e1104b8b67e13d452bbd20d13b0_l3.png)
![Rendered by QuickLaTeX.com \left(\begin{array}{ccc|c} 3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&1&2&-5 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5F_3-F_2} \end{array} \left( \begin{array}{ccc|c}3&-1&1& 2 \\[2ex] 0&5&10&5\\[2ex] 0&0&0&-30\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4deec2426c0b9bb0b8e8a3d95155fd9_l3.png)
Bu nedenle aşağıdaki denklem sistemini elde ettik:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3a_1 -a_2+a_3 = 2 \\[2ex] 5a_2 +10a_3=5\\[2ex] 0 = -30 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e537d5c481ceedeaebf95334d72199ad_l3.png)
Ancak bilinmeyenlerin aldığı değerler ne olursa olsun 0 hiçbir zaman -30’a eşit olmayacağından son denklem asla sağlanamaz. Bu nedenle sistemin çözümü yoktur ve bu, vektörü hesaplayacak doğrusal bir kombinasyonun olmadığı anlamına gelir.
![]()