Tüm doğrusal bağımsız ve bağımlı vektörler

Bu sayfada doğrusal bağımsız ve doğrusal bağımlı vektörlerin ne olduğunu açıklıyoruz. Ayrıca bir vektör kümesinin doğrusal bağımlı mı yoksa bağımsız mı olduğunu nasıl anlayacağınıza dair örnekler göreceksiniz. Ayrıca, doğrusal bağımsızlık ve bağımlılık konusunda adım adım alıştırmalar ve çözülmüş problemler bulacaksınız.

Doğrusal bağımsız vektörler nelerdir?

Hiçbiri diğerlerinin doğrusal birleşimi olarak yazılamıyorsa, bir serbest vektör kümesi doğrusal olarak bağımsızdır .

Başka bir deyişle, bir dizi vektör verildiğinde

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Aşağıdaki denklemin tek çözümü ise bunlar doğrusal olarak bağımsızdır:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

Bunların hepsi katsayılar

$a_i$

0’a eşit:

$a_1=a_2=\dots = a_n=0$

Geometrik olarak iki vektör aynı yöne sahip değillerse, yani paralel değillerse doğrusal olarak bağımsızdırlar.

Kısaca anlatmak gerekirse bazen doğrudan bunların LI vektörleri olduğunu söyleriz. Veya vektörlerin doğrusal bağımsızlığa sahip olduğunu.

Doğrusal bağımlı vektörler nelerdir?

Açıkçası, doğrusal olarak bağımlı vektörler, doğrusal olarak bağımsız vektörlerin tersi anlamına gelir. Bu nedenle tanımı şu şekildedir:

Düzlemin serbest vektörlerinden oluşan bir küme, bunlardan herhangi biri sistemi oluşturan diğer vektörlerin doğrusal bir kombinasyonu olarak ifade edilebiliyorsa doğrusal olarak bağımlıdır .

Başka bir deyişle, bir dizi vektör verildiğinde

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

Aşağıdaki denklemin bir çözümü varsa bunlar doğrusal olarak bağımlıdır:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

belirli bir katsayıya sahip olan

$a_i$

0’dan farklıdır:

$a_i\neq 0$

Bunun tersi de doğrudur: Eğer bir vektör diğer vektörlerin doğrusal birleşimi ise, o zaman kümedeki tüm vektörler doğrusal olarak bağımlıdır.

Ek olarak, eğer iki vektör paralelse, bu onların doğrusal olarak bağımlı olduğu anlamına gelir.

Bazen bunlar kısaltılır ve basitçe LD vektörleri olarak adlandırılır. Veya vektörlerin doğrusal bir bağımlılığı olduğu bile.

Vektörlerin doğrusal olarak bağımlı mı yoksa bağımsız mı olduğunu nasıl bileceğimize dair örnek

Daha sonra doğrusal olarak bağımlı ve bağımsız vektörlerin tipik bir örneğini göreceğiz.

Aşağıdaki 3 3 boyutlu vektörün doğrusal bağımlılığa mı yoksa bağımsızlığa mı sahip olduğunu belirleyin:

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

Öncelikle doğrusal kombinasyon koşulunu belirtmemiz gerekir:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

Şimdi her vektörü koordinatlarıyla değiştiriyoruz. Sıfır vektörüne karşılık gelen sıfır gibi:

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

Katsayılar vektörleri çarptığı için aşağıdaki ifade eşdeğerdir:

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

Vektörleri ekliyoruz:

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

Yakından bakarsak, sol vektörün her koordinatı sağ vektörün her koordinatına eşit olması gerektiğinden önceki ifade 3 denkleme karşılık gelir. Dolayısıyla 3 bilinmeyenli 3 denklemden oluşan homojen bir sistemimiz var:

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

O halde yapmamız gereken tek şey bilinmeyenleri eşit olan denklem sistemini çözmektir.

$a_1, a_2$

$a_3.$

Bunu yapmak için herhangi bir yöntemi kullanabilirsiniz (ikame yöntemi, Gaus yöntemi, Cramer kuralı vb.). Ancak vektörlerin LI mı yoksa LD mi olduğunu bilmek için önemsiz çözümden başka bir çözümün olup olmadığını belirlemek yeterlidir (tüm katsayılar sıfıra eşittir). BU YÜZDEN:

Vektörlerin bileşenlerinden oluşan matrisin determinantı sıfırdan farklı ise bu, denklem sisteminin tek bir çözümü olduğu anlamına gelir (
$a_1=a_2=a_3=\dots=0$

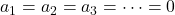
) ve dolayısıyla vektörler doğrusal olarak bağımsızdır
Öte yandan, vektörlerin bileşenlerinden oluşan matrisin determinantının sıfıra eşit olması, denklem sisteminin birden fazla çözümü olduğu ve dolayısıyla vektörlerin doğrusal bağımlı olduğu anlamına gelir.

Yani hesaplanması gereken tek şey vektörlerin koordinatları olan determinanttır (3×3 determinant olduğundan Sarrus kuralıyla çözülebilir). Bu determinant önceki denklem sisteminin katsayılarına karşılık gelir:

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

Bu durumda determinant 0’dan farklıdır, dolayısıyla vektörler doğrusal olarak bağımsızdır .

Bu nedenle denklem sisteminin mümkün olan tek çözümü, tüm bilinmeyenlerin sıfıra eşit olduğu önemsiz çözümdür:

$a_1=a_2=a_3=0$

Doğrusal bağımlı ve bağımsız vektörlerin özellikleri

Vektörlerin doğrusal bağımlılığı veya bağımsızlığı aşağıdaki özelliklere sahiptir:

İki orantılı vektör paraleldir ve aynı yöne sahip oldukları için doğrusal olarak bağımlıdırlar.

Benzer şekilde iki vektör aynı yöne sahip değilse veya orantılı değilse doğrusal olarak bağımsızdırlar.

Üç ortak düzlemli vektör (aynı düzlemde olan) doğrusal olarak bağımsızdır.

Boş vektör
$(\vv{\text{v}}=(0,0,0))$

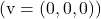
herhangi bir vektöre doğrusal olarak bağımlıdır.

Doğrusal olarak bağımsız vektörlerden oluşan bir küme, bir vektör uzayı oluşturur ve bir vektör tabanı oluşturur. Üç vektör birbirine dik ise bu bir dik tabandır. Ve eğer modülü de 1’e eşitse, bu ortonormal bir tabana karşılık gelir.

Çözülmüş doğrusal bağımlılık ve bağımsızlık egzersizleri

Aşağıda doğrusal bağımlı ve bağımsız vektörlerle ilgili pratik yapabileceğiniz birkaç çözülmüş alıştırma var.

1. Egzersiz

Aşağıdaki vektörlerin doğrusal olarak bağımlı mı yoksa bağımsız mı olduğunu belirleyin:

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

Çözümü görün

İlk önce doğrusal kombinasyon koşulunu ortaya koyuyoruz:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

Önceki eşitlik aşağıdaki doğrusal denklem sistemine karşılık gelir:

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

Denklem sistemini ifade ettikten sonra matrisin determinantını terimleriyle çözüyoruz:

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

Bu durumda determinant 0’dan farklıdır, yani üç vektör birbirinden doğrusal olarak bağımsızdır .

Alıştırma 2

Aşağıdaki vektörleri doğrusal olarak bağımlı veya bağımsız olarak sınıflandırın:

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

Çözümü görün

Öncelikle doğrusal kombinasyonun denklemini ortaya koyuyoruz:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

Önceki eşitlikten aşağıdaki homojen denklem sistemini elde ederiz:

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

Denklem sistemini belirledikten sonra matrisin determinantını vektörlerin koordinatlarıyla çözüyoruz:

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

Bu durumda determinant 0’a eşit olduğundan üç vektör birbirine doğrusal olarak bağlıdır .

Alıştırma 3

Aşağıdaki üç vektör için hangi vektör çiftlerinin doğrusal bağımlı, hangi çiftlerin doğrusal bağımsız olduğunu belirtin.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

Çözümü görün

Bir vektör çiftinin doğrusal olarak bağımlı mı yoksa bağımsız mı olduğunu anlamanın en basit yolu, bunların orantılı olup olmadığını kontrol etmektir.

İlk önce vektörü kontrol ediyoruz

$\vv{\text{u}}$

vektör ile

$\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

İkinci olarak vektörü kontrol ediyoruz

$\vv{\text{u}}$

vektör ile

$\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

Son olarak vektörü test ediyoruz

$\vv{\text{v}}$

vektör ile

$\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

Dolayısıyla birbirine doğrusal olarak bağlı olan tek vektör çifti

$\vv{\text{v}}$

$\vv{\text{w}}.$

Ayrıca aralarındaki ilişki şu şekildedir:

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

Veya eşdeğer:

$\vv{\text{w}}= -2\vv{\text{v}}$

Öte yandan diğer vektör çiftleri doğrusal olarak bağımsızdır.

Alıştırma 4

Aşağıdaki 4 vektörün birbirine doğrusal bağımlılığını veya bağımsızlığını inceleyin:

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

Çözümü görün

İlk önce doğrusal kombinasyon koşulunu ortaya koyuyoruz:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

Bu durumda 4 bilinmeyenli 3 denklemden oluşan bir sistemimiz var:

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

Yalnızca kare matrisler belirlenebildiği için tüm sistem matrisinin determinantını çözemeyiz. Bu nedenle 3×3 determinantların tüm olası kombinasyonlarını hesaplamalı ve bunlardan birinin 0’a eşit olup olmadığına bakmalıyız; bu durumda vektörler doğrusal olarak bağımlı olacaktır; diğer taraftan, tüm determinantlar 0’dan farklıysa 4 vektör doğrusal bağımsız olsun.

Katsayıların determinantını hesaplıyoruz

$a_1, a_2$

$a_3:$

$\displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}$

İlk 3 katsayıların (veya ilk 3 vektörün) determinantı sıfırdan farklıdır. Şimdi katsayıların determinantını deneyelim

$a_1, a_2$

$a_4:$

$\displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}$

Sıfır determinantı elde ettik, dolayısıyla diğer determinantları hesaplamaya gerek yok çünkü 4 vektörün doğrusal olarak bağımlı olduğunu zaten biliyoruz.