Bir matris nasıl köşegenleştirilir -

Bu sayfada köşegenleştirilebilir matrisler hakkında her şeyi bulacaksınız: ne oldukları, ne zaman köşegenleştirilebileceği ve ne zaman köşegenleştirilemeyeceği, matrisleri köşegenleştirme yöntemi, bu belirli matrislerin uygulamaları ve özellikleri, vb. Hatta adım adım çözülmüş birkaç alıştırmanız bile var, böylece pratik yapabilir ve bunların nasıl köşegenleştirildiğini mükemmel bir şekilde anlayabilirsiniz. Son olarak, çok sık kullanıldığı için MATLAB bilgisayar programıyla matris köşegenleştirmelerinin nasıl yapıldığını da öğreniyoruz.

Köşegenleştirilebilir matris nedir?

Aşağıda göreceğimiz gibi, bir matrisin köşegenleştirilmesi lineer cebir alanında oldukça faydalıdır. Bu yüzden birçok kişi şunu soruyor: Matris köşegenleştirme nedir? Köşegenleştirilebilir bir matrisin tanımı şöyledir:

Köşegenleştirilebilir bir matris, köşegen bir matrise, yani ana köşegen dışında sıfırlarla dolu bir matrise dönüştürülebilen bir kare matristir. Matrislerin köşegenleştirilmesi şu şekilde bozulur:

$A = PDP^{-1}$

Veya eşdeğer,

$D = P^{-1}AP$

Altın

$A$

köşegenleştirilecek matris,

$P$

sütunları özvektörleri (veya özvektörleri) olan matristir.

$A$

$P^{-1}$

ters matrisi ve

$D$

özdeğerlerinin (veya özdeğerlerinin) oluşturduğu diyagonal matristir

$A$

Matris

$P$

baz değişim matrisi gibi davranır, yani aslında bu formülle tabanı matrise dönüştürüyoruz

$A$

, böylece matris köşegen bir matris haline gelir (

$D$

) yeni üssünde.

Bu nedenle matris

$A$

ve matris

$D$

Bunlar benzer matrislerdir. Ve açıkçası,

$P$

Düzenli veya dejenere olmayan bir matristir.

Bir matrisi ne zaman köşegenleştirebilirsiniz?

Tüm matrisler köşegenleştirilemez; yalnızca belirli özellikleri karşılayan matrisler köşegenleştirilebilir. Bir matrisin köşegenleştirilebilir olup olmadığını farklı yollarla anlayabilirsiniz:

n mertebesinden bir kare matris, n tane doğrusal bağımsız özvektöre (veya özvektöre) sahipse veya başka bir deyişle, bu vektörler bir temel oluşturuyorsa köşegenleştirilebilir. Bunun nedeni matrisin
$P$

Bir matrisi köşegenleştirmek için kullanılan matrisin özvektörleri tarafından oluşturulur. Özvektörlerin LI olup olmadığını bilmek için matrisin determinantının olması yeterlidir.

$P$

0’dan farklıdır, bu da matrisin maksimum dereceye sahip olduğu anlamına gelir.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

Özdeğerlerin ve özvektörlerin bir özelliği, farklı özdeğerlerin özvektörlerinin doğrusal olarak bağımsız olmasıdır. Dolayısıyla matrisin tüm özdeğerleri benzersizse matris köşegenleştirilebilir.

Bir matrisin köşegen bir matriste yer alıp alamayacağını belirlemenin başka bir yolu cebirsel ve geometrik çoklukların kullanılmasıdır. Cebirsel çokluk, bir özdeğerin (veya özdeğerin) tekrarlanma sayısıdır ve geometrik çokluk, matrisin çekirdeğinin (veya çekirdeğinin), özdeğerin ana köşegeninden çıkarılmasıyla elde edilen boyutudur. Dolayısıyla, her bir özdeğer için cebirsel çokluk geometrik çokluğa eşitse , matris köşegenleştirilebilir.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

Son olarak, simetrik matrislerin gerçel sayılarla köşegenleştirilmesini garanti eden bir teorem vardır: Spektral teorem. Başka bir deyişle, herhangi bir gerçek ve simetrik matris köşegenleştirilebilir .

Bir matris nasıl köşegenleştirilir

Bir matrisi köşegenleştirme prosedürü, bir matrisin özdeğerlerini (veya özdeğerlerini) ve özvektörlerini (veya özvektörlerini) bulmaya dayanır. Bu nedenle herhangi bir matrisin özdeğerlerini (veya özdeğerlerini) ve özvektörlerini (veya özvektörlerini) nasıl hesaplayacağınızı öğrenmeniz önemlidir. Bunları nasıl bulacağınızı ve hesaplamaları çok daha kolaylaştıran bazı püf noktalarını adım adım açıkladığımız bağlantıya tıklayarak nasıl yapıldığını hatırlayabilirsiniz. Ayrıca pratik yapabileceğiniz çözümlü alıştırmalar da bulacaksınız.

Aşağıdaki yöntemle herhangi bir boyuttaki bir matrisi köşegenleştirebilirsiniz: 2×2, 3×3, 4×4 vb. Bir matrisi köşegenleştirmek için izlenecek adımlar şunlardır:

Matrisin özdeğerlerini (veya özdeğerlerini) elde edin.
Her bir özdeğerle ilişkili özvektörü hesaplayın.
Matrisin oluşturulması
$P$

Sütunları köşegenleştirilecek matrisin özvektörleridir.
Matrisin köşegenleştirilebildiğini kontrol edin (önceki bölümde açıklanan koşullardan birini karşılamalıdır).
Çapraz matrisi oluşturun
$D$

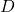
1. adımda bulunan özdeğerler olan ana köşegendekiler hariç tüm elemanları 0 olan.

Uyarı: Matrisin özvektörleri

$P$

herhangi bir sıraya yerleştirilebilir ancak köşegen matrisin özdeğerleri

$D$

Aynı sıraya yerleştirilmelidirler. Örneğin köşegen matrisin ilk öz değeri

$D$

matrisin ilk sütununun özvektörüne karşılık gelen olmalıdır

$P$

Aşağıda pratik yapabileceğiniz birkaç adım adım matris köşegenleştirme alıştırmaları bulunmaktadır.

Matris köşegenleştirme alıştırmaları çözüldü

1. Egzersiz

Aşağıdaki 2×2 boyutlu kare matrisi köşegenleştirin:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

Çözümü görün

İlk önce A matrisinin özdeğerlerini belirlemeliyiz. Bu nedenle aşağıdaki determinantı çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

Şimdi karakteristik polinomun köklerini hesaplayalım:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

Özdeğerler elde edildikten sonra her biriyle ilişkili özvektörü hesaplarız. İlk olarak, özdeğer 1’e karşılık gelen özvektör:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

Daha sonra özdeğer 4 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

Matris’i oluşturuyoruz

$P$

matrisin özvektörleri tarafından oluşturulan:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

Tüm özdeğerler farklı olduğundan A matrisi köşegenleştirilebilir. Dolayısıyla karşılık gelen köşegen matris, ana köşegen üzerinde özdeğerlere sahip olan matristir:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Özvektörlerin matrise yerleştirildiği sırada özdeğerlerin de aynı sıraya yerleştirilmesi gerektiğini unutmayın.

$P$

Sonuç olarak, temel değişim matrisi ve köşegenleştirilmiş matris şu şekildedir:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

Alıştırma 2

Aşağıdaki 2. dereceden kare matrisi köşegenleştirin:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

Çözümü görün

İlk önce A matrisinin özdeğerlerini belirlemeliyiz. Bu nedenle aşağıdaki determinantı çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

Şimdi karakteristik polinomun köklerini hesaplayalım:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

Özdeğerler elde edildikten sonra her biriyle ilişkili özvektörü hesaplarız. İlk olarak, özdeğer -1’e karşılık gelen özvektör:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

Daha sonra özdeğer 2 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

Matris’i oluşturuyoruz

$P$

matrisin özvektörleri tarafından oluşturulan:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

Tüm özdeğerler birbirinden farklı olduğundan A matrisi köşegenleştirilebilir. Dolayısıyla karşılık gelen köşegen matris, ana köşegendeki özdeğerleri içeren matristir:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Özvektörlerin matrise yerleştirildiği sırada özdeğerlerin de aynı sıraya yerleştirilmesi gerektiğini unutmayın.

$P$

Sonuç olarak, temel değişim matrisi ve köşegenleştirilmiş matris şu şekildedir:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

Alıştırma 3

Aşağıdaki 3×3 boyutlu kare matrisi köşegenleştirin:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

Çözümü görün

İlk adım, A matrisinin özdeğerlerini bulmaktan oluşur. Bu nedenle, aşağıdaki matrisin determinantını çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

Şimdi karakteristik polinomun köklerini hesaplamamız gerekiyor. Üçüncü dereceden bir polinom olduğu için Ruffini kuralını uyguluyoruz:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

Daha sonra elde edilen polinomun köklerini buluruz:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

Yani matrisin özdeğerleri şöyledir:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

Özdeğerler bulunduktan sonra her biriyle ilişkili özvektörü hesaplarız. İlk olarak, özdeğer 1’e karşılık gelen özvektör:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

Daha sonra özdeğer 3 ile ilişkili özvektörü hesaplarız:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Ve son olarak özdeğer 4 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

Matris’i oluşturuyoruz

$P$

matrisin özvektörleri tarafından oluşturulan:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

Tüm özdeğerler birbirinden farklı olduğundan A matrisi köşegenleştirilebilir. Dolayısıyla karşılık gelen köşegen matris, ana köşegen üzerinde özdeğerlere sahip olan matristir:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Özvektörlerin matrise yerleştirildiği sırada özdeğerlerin de aynı sıraya yerleştirilmesi gerektiğini unutmayın.

$P$

Kısaca temel değişim matrisi ve köşegenleştirilmiş matris şöyledir:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

Alıştırma 4

Mümkünse aşağıdaki 3. mertebeden kare matrisi köşegenleştirin:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

Çözümü görün

İlk adım, A matrisinin özdeğerlerini bulmaktan oluşur. Bu nedenle, aşağıdaki matrisin determinantını çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

Şimdi minimum polinomun köklerini hesaplamamız gerekiyor. Üçüncü dereceden bir polinom olduğundan, bunu çarpanlara ayırmak için Ruffini kuralını uyguluyoruz:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

Daha sonra elde edilen polinomun köklerini buluruz:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

Yani matrisin özdeğerleri şöyledir:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

-2’nin özdeğeri basit cebirsel çokluğa sahipken, 2’nin özdeğeri çift katlıdır.

Özdeğerler bulunduktan sonra her biriyle ilişkili özvektörü hesaplarız. İlk olarak, özdeğer -2’ye karşılık gelen özvektör:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

Şimdi özdeğerler 2 ile ilişkili özvektörleri hesaplayalım.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

Özdeğer 2 iki kez tekrarlandığından, altuzay (veya özuzay) denklemlerini karşılayan başka bir özvektör hesaplamamız gerekir:

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

Matris’i oluşturuyoruz

$P$

matrisin üç özvektörünün oluşturduğu:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

Bununla birlikte, üç vektör doğrusal olarak bağımsız değildir, çünkü özdeğeri 2 olan iki özvektör açıkça birbirinin doğrusal bir kombinasyonudur. Bu aynı zamanda matrisin determinantı nedeniyle de gösterilebilir.

$P$

0’a eşittir (sıfırlarla dolu bir satıra sahiptir):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

Bu nedenle, özvektörler doğrusal olarak bağımlı olduğundan, A matrisi köşegenleştirilemez .

Alıştırma 5

Mümkünse, aşağıdaki 3×3 boyutunda kare matrisi köşegenleştirin:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

Çözümü görün

İlk adım, A matrisinin özdeğerlerini bulmaktan oluşur. Bu nedenle, aşağıdaki matrisin determinantını çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

İlk satır 3 hariç tamamen sıfırlardan oluştuğundan, matrisin determinantını kofaktörlere (veya eklere) göre çözmek için bundan yararlanacağız:

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

Şimdi karakteristik polinomun köklerini hesaplamamız gerekiyor. Parantezleri çarpmamak daha iyidir çünkü o zaman üçüncü dereceden bir polinom elde edersiniz. Öte yandan, eğer iki faktör ayrı ayrı çözülürse özdeğerleri elde etmek daha kolaydır:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

Yani matrisin özdeğerleri şöyledir:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

Özdeğerler bulunduktan sonra her biriyle ilişkili özvektörü hesaplarız. İlk olarak, özdeğer 1’e karşılık gelen özvektör:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

Daha sonra özdeğerler 3 ile ilişkili özvektörleri hesaplıyoruz:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

Özdeğer 3 iki kez tekrarlandığından, özuzay denklemlerini karşılayan başka bir özvektör hesaplamamız gerekir:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

Matris’i oluşturuyoruz

$P$

matrisin özvektörleri tarafından oluşturulan:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

Alıştırma 4’ten farklı olarak, bu durumda özdeğer 3’ün cebirsel çokluğu iki katı olmasına rağmen doğrusal olarak bağımsız 3 vektör oluşturabildik. Bu, matrisin determinantının şu şekilde olduğu görülerek doğrulanabilir:

$P$

0’dan farklı bir sonuç verir:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

Böylece A matrisinin köşegen ayrıştırmasını gerçekleştirebiliriz. Ve karşılık gelen köşegen matris, ana köşegen üzerinde özdeğerlere sahip olan matristir:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Özvektörlerin matrise yerleştirildiği sırada özdeğerlerin de aynı sıraya yerleştirilmesi gerektiğini unutmayın.

$P$

Kısaca matrisi köşegenleştirmek için gereken temel değişim matrisi ve köşegenleştirilmiş hali şunlardır:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

Alıştırma 6

Mümkünse aşağıdaki 4×4 boyut matrisinin köşegenleştirmesini yapın:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Çözümü görün

İlk adım, A matrisinin özdeğerlerini bulmaktan oluşur. Bu nedenle, aşağıdaki matrisin determinantını çözerek karakteristik denklemi hesaplıyoruz:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

Bu durumda, determinantın son sütunu bir öğe dışında yalnızca sıfırlardan oluşur; bu nedenle, determinantı bu sütun aracılığıyla kofaktörlere göre hesaplamak için bundan yararlanacağız:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

Şimdi karakteristik polinomun köklerini hesaplamamız gerekiyor. Parantezlerin çarpımını yapmamak daha iyidir çünkü o zaman dördüncü dereceden bir polinom elde edersiniz. Ancak iki faktör ayrı ayrı çözülürse özdeğerleri hesaplamak daha kolaydır:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

Yani matrisin özdeğerleri şöyledir:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

Tüm özdeğerler bulunduktan sonra özvektörlere doğru ilerliyoruz. Özdeğer 0 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Özdeğer -3 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Özdeğer 2 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

Özdeğer 5 ile ilişkili özvektörü hesaplıyoruz:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

Matris yapıyoruz

$P$

, matrisin özvektörlerinden oluşur:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

Tüm özdeğerler birbirinden farklı olduğundan A matrisi köşegenleştirilebilir. Dolayısıyla karşılık gelen köşegen matris, ana köşegen üzerinde özdeğerlere sahip olan matristir:

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Özvektörlerin matriste konumlandırılmasıyla özdeğerlerin aynı sıraya yerleştirilmesi gerektiğini unutmayın.

$P$

Özetle, A matrisini ve matrisi köşegen formda köşegenleştirmek için gereken temel matris değişiklikleri şunlardır:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

Köşegenleştirilebilir matrislerin uygulamaları

Buraya kadar geldiyseniz muhtemelen şunu merak ediyorsunuzdur: Köşegenleştirilebilir bir matris ne işe yarar?

Köşegenleştirilebilir matrisler çok faydalıdır ve matematikte yaygın olarak kullanılır. Bunun nedeni, diyagonal bir matrisin pratikte sıfırlarla dolu olması ve bu nedenle hesaplamaları çok daha kolay hale getirmesidir.

Bunun açık bir örneği köşegenleştirilebilir matrislerin kuvvetleridir, çünkü sonuçları aşağıdaki formülle basitleştirilmiştir:

$\displaystyle A^k=PD^kP^{-1}$

Bu eşitlik tümevarımla kolaylıkla kanıtlanabilir. Bu nedenle matrisi yükseltmek yeterlidir

$D$

katılımcıya. Ve bu bir köşegen matris olduğu için işlem, ana köşegenin her bir terimini üsse yükseltmeye indirgenir:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

Köşegenleştirilebilir bir matrisin kuvveti örneği

Daha iyi anlamak için örnek olarak köşegenleştirilebilir bir matrisin gücünü hesaplayacağız:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

Temel Değişim Matrisi

$P$

özvektörleri ve köşegenleştirilmiş matris tarafından oluşturulan

$D$

, kendi değerlerinden oluşan, şunlardır:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

Yani bir örnek vermek gerekirse, A matrisinin 7’ye yükseltilmesi şuna eşdeğerdir:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

Şimdi matrisi ters çeviriyoruz

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Matrisin gücünü çözüyoruz

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

Ve son olarak matrislerin çarpımlarını gerçekleştiriyoruz:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

Gördüğünüz gibi kuvveti köşegen bir matrisle hesaplamak, aynı matrisi arka arkaya yedi kez çarpmaktan daha uygundur. Daha sonra çok daha büyük üslü değerlerle hayal edin.

Köşegenleştirilebilir matrislerin özellikleri

Bu tür matrisin özellikleri şunlardır:

Matris ise
$A$

köşegenleştirilebilir, herhangi bir kuvvet

$A$

.

Hemen hemen tüm matrisler karmaşık bir ortamda köşegenleştirilebilir
$\mathbb{C}$

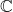
. Aşağıda hiçbir zaman köşegenleştirilemeyen istisnalar bulunmaktadır.

Matris ise
$P$

dik bir matris ise, o zaman matris deriz

$A$

ortogonal olarak köşegenleştirilebilir ve bu nedenle denklem yeniden yazılabilir:

$\displaystyle A=PDP^t$

Bir matris, ancak ve ancak normal bir matris olması durumunda üniter bir matris tarafından köşegenleştirilebilir.

Köşegenleştirilebilen iki matris verildiğinde, bunlar ancak ve ancak aynı anda köşegenleştirilebiliyorlarsa, yani özvektörlerin (veya özvektörlerin) aynı ortonormal tabanını paylaşıyorlarsa değiştirilebilirler.

Bir endomorfizm köşegenleştirilebilirse, benzerlik yoluyla köşegenleştirilebilir diyoruz. Bununla birlikte, tüm endomorfizmler köşegenleştirilebilir değildir veya başka bir deyişle, bir endomorfizmin köşegenleştirilmesi garanti edilmez.

Eşzamanlı Köşegenleştirme

Bir matris kümesinin, bu kümedeki herhangi bir matrisin köşegenleştirilmesi için temel görevi gören tersinir bir matris mevcut olması durumunda, aynı anda köşegenleştirilebildiği söylenir. Başka bir deyişle, eğer iki matris aynı özvektör bazında köşegenleşiyorsa, bu onların aynı anda köşegenleştirilebildiği anlamına gelir.

Ek olarak, matris köşegenleştirmenin özelliklerinde de belirttiğimiz gibi, eğer iki matris aynı anda köşegenleşebiliyorsa birbirleriyle yer değiştirmeleri gerekir.

Örneğin, aşağıdaki iki matris değiştirilebilirdir, dolayısıyla aynı özvektörler veya özvektörler bazında köşegenleşirler.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

Aynı özvektörlere sahip olsalar bile, bu aynı özdeğerlere sahip oldukları anlamına gelmez. Aslında yukarıdaki A ve B matrisleri benzer özvektörlere sahip olmalarına rağmen farklı özdeğerlere sahiptirler.

Köşegenleştirilemeyen matrisler

Karmaşık sayı ortamında matrislerin büyük çoğunluğu köşegenleştirilebilir olmasına rağmen, bazı matrisler hiçbir zaman köşegenleştirilemez.

Bu gerçek, bir özdeğerin (veya özdeğerin) cebirsel çokluğu geometrik çokluk ile örtüşmediğinde ortaya çıkar.

Örneğin aşağıdaki matris hiçbir şekilde köşegenleştirilemez, “köşegenleştirilemez”:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

Ek olarak, gerçek sayı ortamında köşegenleştirme yeteneğine sahip olmayan ancak karmaşık sayılarla çalışırken aşağıdaki matris gibi köşegenleşen matrisler de vardır:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

Son olarak, tamamen köşegenleştirilemeyen ancak biraz daha karmaşık olan bazı matris bloğu köşegenleştirme prosedürleri vardır. En iyi bilinen yöntem Jordan’ın kanonik formuyla köşegenleştirmedir.

MATLAB ile bir matrisi köşegenleştirme

Matrislerin köşegenleştirilmesi söz konusu olduğunda bilgisayar programları çok kullanışlıdır, özellikle de matrisler çok büyükse. Ve en iyi bilinen yazılım kesinlikle MATLAB’dır , bu yüzden bu programı kullanarak bir matrisi köşegensel olarak nasıl çarpanlara ayıracağımızı göreceğiz.

MATLAB ile bir matrisi köşegenleştirmek için kullanılan talimat şöyledir:

$\displaystyle \text{[P, D] = eig(A)}$

Altın

$A$

köşegenleştirilecek matristir ve

$P$

$D$

programın döndürdüğü matrisler şunlardır:

$P$

özvektörlerin oluşturduğu matristir ve

$D$

ana köşegen terimleri özdeğerler olan köşegen formdaki matristir.

Bu nedenle programa bu kodu girmeniz yeterlidir.

Öte yandan, yalnızca özdeğerleri bilmek istiyorsanız aşağıdaki ifadeyi kullanabilirsiniz:

$\displaystyle e= eig(A)}$

Altın

$e$

MATLAB’ın matrisin özdeğerleriyle döndürdüğü sütun vektörüdür

$A$

Köşegenleştirilebilir matris nedir?

Bir matrisi ne zaman köşegenleştirebilirsiniz?

Bir matris nasıl köşegenleştirilir

Matris köşegenleştirme alıştırmaları çözüldü

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Köşegenleştirilebilir matrislerin uygulamaları

Köşegenleştirilebilir bir matrisin kuvveti örneği

Köşegenleştirilebilir matrislerin özellikleri

Eşzamanlı Köşegenleştirme

Köşegenleştirilemeyen matrisler

MATLAB ile bir matrisi köşegenleştirme

Yorum bırakın Yanıtı iptal et