▷ Bir sayının polinom ayrıştırması nasıl yapılır ✅

Bu sayfada bir sayının polinom ayrıştırmasının (veya ifadesinin) nasıl yapılacağını açıklıyoruz. Burada polinom ayrışımı örneklerini görebilir ve ayrıca uygulamaya yönelik adım adım çözülmüş alıştırmalar bulacaksınız.

Bir sayının polinom ayrışımı nedir?

Matematikte, bir sayının polinom ayrışımı, bu sayının bir toplamla ifade edilmesinden oluşur; böylece toplamın her terimi, sayının her basamağının 10 tabanının bir kuvveti ile çarpımı olur.

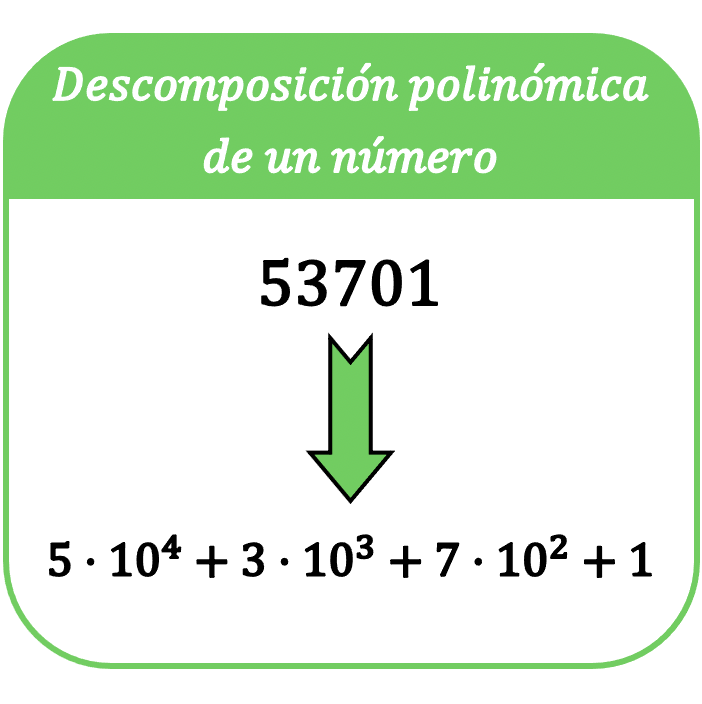
Bir sayının polinom ayrışımı terimi aynı zamanda bir sayının polinom ifadesi olarak da bilinir.

Polinom ayrıştırması nasıl yapılır

Bir sayının polinom ayrıştırmasını gerçekleştirmek için sayının her basamağını sağdaki basamak sayısına yükseltilmiş 10 ile çarpmanız gerekir.

Örneğin aşağıdaki sayının polinom ayrışmasını hesaplamak istiyorsak:

$86293$

Bu durumda 8 sayısı beşinci sırada yer aldığından sağında 4 rakam bulunur. Bu nedenle sekizi on üzeri dörtle çarpmamız gerekir:

$8\cdot 10^4$

Bu nedenle, 86293 sayısını polinom olarak ayrıştırmak için, aynı işlemi sayının tüm rakamlarıyla yapmalı ve tüm çarpmaları bir toplam biçiminde ifade etmelisiniz:

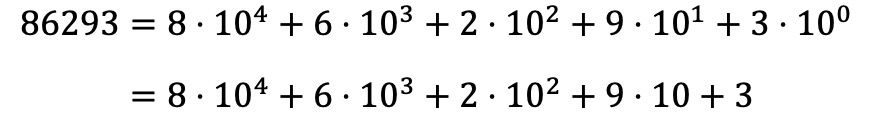
10 ^0’ın kuvvetinin kaybolduğuna dikkat edin, çünkü kuvvetlerin özelliklerine göre, 0’a yükseltilen herhangi bir sayı 1’e eşittir, dolayısıyla 10 ⁰ = 1’dir.

Öte yandan, bir sayının polinom ayrışmasını çarpımsal ayrışımından da bulabilirsiniz:

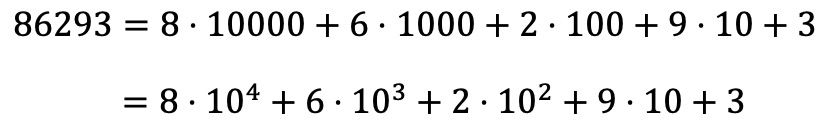
İlkokul için doğal sayıların polinom ayrışımı

Sayıların polinom ayrışımı örnekleri

Bir sayının polinom ayrıştırmasının nasıl yapıldığını gördükten sonra, kavramı tam olarak anlamak için bu tür işlemin farklı örneklerini göreceğiz.

3641’in polinom ayrışımı:

$3641 = 3\cdot 10^3 +6 \cdot 10^2 + 4\cdot 10 + 1$

56912’nin polinom ayrışımı:

$56912 = 5\cdot 10^4 +6\cdot 10^3 +9 \cdot 10^2 + 1\cdot 10 + 2$

27084’ün polinom ayrışımı:

$\begin{aligned} 27084 &= 2\cdot 10^4 +7\cdot 10^3 +0\cdot 10^2 + 8\cdot 10 + 4 \\[2ex] & = 2\cdot 10^4 +7\cdot 10^3 + 8\cdot 10 + 4 \end{aligned}$

Bu son örnekte, sıfırla çarpılan herhangi bir sayı birbirini götürdüğü için üçüncü çarpımı basitleştirebiliriz.

Ondalık sayıların polinom ayrışımı

Az önce doğal sayıların polinom ayrıştırmasının nasıl gerçekleştirileceğini gördük. Ama… ondalık bir sayıyı polinom olarak nasıl ayrıştırırsınız?

Ondalık sayılarla polinom ayrıştırması, tam sayılarla aynı şekilde yapılır, ancak ek olarak, her ondalık basamağın çarpımını, üssü adı geçen rakamın negatif olduğu ondalık konum olan 10 tabanının kuvvetiyle çarparak toplarız. imza.

Kelimelerle açıklamak çok karmaşık görünebilir, ancak bir örnekle her şeyin daha iyi anlaşıldığını göreceksiniz:

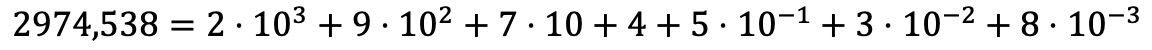
Çözülmüş polinom ayrıştırma alıştırmaları

Polinom ayrıştırmalarını pratik yapabilmeniz için adım adım çözülen birkaç alıştırma hazırladık.

Aklınıza takılan her türlü soruyu bize yorumlarda sorabileceğinizi unutmayın! 🤔🤔🤔

1. Egzersiz

Aşağıdaki sayıların polinom ayrıştırmasını gerçekleştirin:

$\text{A)} \ 7935$

$\text{B)} \ 1548$

$\text{C)} \ 55476$

$\text{D)} \ 287694$

Çözümü görün

Herhangi bir sayının polinom ayrışımı bulmak için o sayının her basamağını sağdaki basamak sayısıyla 10 ile çarpın, ardından tüm çarpımları ekleyin. Henüz:

$\text{A)} \ 7935 = 7 \cdot 10^3+ 9\cdot 10^2 +3 \cdot 10 +5$

$\text{B)} \ 1548 = 1 \cdot 10^3+ 5\cdot 10^2 +4 \cdot 10 +8$

$\text{C)} \ 55476 = 5\cdot 10^4+ 5 \cdot 10^3+ 4\cdot 10^2 +7\cdot 10 +6$

$\text{D)} \ 287694 = 2\cdot 10^5+8\cdot 10^4+ 7 \cdot 10^3+ 6\cdot 10^2 +9\cdot 10 +4$

Alıştırma 2

Aşağıdaki sayıların polinom ayrışımını bulun:

$\text{A)} \ 461$

$\text{B)} \ 3030$

$\text{C)} \ 11950$

$\text{D)} \ 8741866$

Çözümü görün

Bir sayıyı polinom olarak ayrıştırmak için, söz konusu sayının her basamağını sağındaki basamak sayısıyla on ile çarpmanız ve ardından tüm çarpımları toplamanız gerekir. Henüz:

$\text{A)} \ 461 = 4\cdot 10^2 +6 \cdot 10 +1$

$\text{B)} \ \begin{aligned} 3030 & = 3 \cdot 10^3+ 0\cdot 10^2 +3 \cdot 10 +0 \\[2ex] &= 3 \cdot 10^3+3 \cdot 10 \end{aligned}$

$\text{C)} \ 11950 = 1\cdot 10^4+ 1 \cdot 10^3+ 9\cdot 10^2 +5\cdot 10$

$\text{D)} \ 8741866 = 8\cdot 10^6+7\cdot 10^5+4\cdot 10^4+ 1 \cdot 10^3+ 8\cdot 10^2 +6\cdot 10 +6$

Alıştırma 3

Aşağıdaki ondalık sayıların polinom ayrışmasını hesaplayın:

$\text{A)} \ 51,63$

$\text{B)} \ 249,99$

$\text{C)} \ 0,82694$

$\text{D)} \ 5,7201$

Çözümü görün

Bu problemde tüm sayılar ondalıktır, dolayısıyla bunları ayrıştırmak için ondalık olmayan her rakamı, ondalık basamağa kadar sahip olduğu rakam sayısına yükseltilmiş 10 ile çarpmanız ve her ondalık rakamı, ondalık konumuna yükseltilmiş 10 ile çarpmanız gerekir. olumsuz bir işaret.

$\text{A)} \ 51,63 = 5 \cdot 10 +1 + 6 \cdot 10^{-1} +3 \cdot 10^{-2}$

$\text{B)} \ 249,99 = 2\cdot 10^2 + 4 \cdot 10 +9 + 9 \cdot 10^{-1} +9 \cdot 10^{-2}$

$\text{C)} \ \begin{aligned} 0,82694 & = 0 + 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\\[2ex] & = 8 \cdot 10^{-1} +2 \cdot 10^{-2}+6\cdot 10^{-3}+9\cdot 10^{-4} +4\cdot 10^{-5}\end{aligned}$

$\text{D)} \ \begin{aligned} 5,7201 & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+0\cdot 10^{-3}+1\cdot 10^{-4}\\[2ex] & = 5 + 7 \cdot 10^{-1} +2 \cdot 10^{-2}+1\cdot 10^{-4} \end{aligned}$

Bir sayının polinom ayrışımı (veya ifadesi)

Bir sayının polinom ayrışımı nedir?

Polinom ayrıştırması nasıl yapılır

Sayıların polinom ayrışımı örnekleri

Ondalık sayıların polinom ayrışımı

Çözülmüş polinom ayrıştırma alıştırmaları

1. Egzersiz

Alıştırma 2

Alıştırma 3

Yorum bırakın Yanıtı iptal et