Newton'un binom (binom teoremi)

Bu sayfada Newton’un binomunun (veya binom teoreminin) ne olduğu ve formülünün ne olduğuna dair açıklama bulacaksınız. Bunun Tartaglia (veya Pascal) üçgeni ile nasıl basitleştirilebileceğini de görebilirsiniz. Ayrıca Newton’un binomuna ve onun tüm özelliklerine ilişkin adım adım çözülmüş alıştırmalar bulacaksınız. Son olarak bu çok özel teoremin kökeninin ardındaki merakı açıklayacağız.

Newton’un binom’u nedir?

Matematikte, iki terimli teorem olarak da bilinen Newton’un binom’u , bir binomun kuvvetini kolayca hesaplamanızı sağlayan bir formüldür. Başka bir deyişle Newton binom’u, (a+b) formundaki cebirsel ifadelerin çözülebileceği bir formülden oluşur.

Açıkçası, bu teorem fizikçi, matematikçi ve filozof Sir Isaac Newton’un adını almıştır. Ancak bu teoremin halihazırda kullanımda olduğu Orta Doğu metinlerinin bulunması nedeniyle bu konuda bazı tartışmalar vardır. Aşağıda bu matematiksel formülün kökenini derinlemesine tartışacağız.

Newton’un binom formülü

Newton’un binomunun tanımında gördüğümüz gibi bu teorem, binomların kuvvetlerini çözmek için kullanılır. Ama… Newton’un binom’u nasıl uygulanır? Veya başka bir deyişle Newton’un binom formülü nedir?

Newton binomunun matematiksel formülü aşağıdaki gibidir:

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

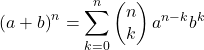
Veya eşdeğer:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

Formül, Newton binom kavramını anlamak için biraz karmaşıktır, bu nedenle daha iyi anlayabilmeniz için en düşük derecedeki binomların kuvvetlerini aşağıda sunduk:

Newton'un binom teoreminin formülü

Gördüğünüz gibi, bir binom’u genişletirken , birinci terimin (a) üsleri azalırken, ikinci terimin (b) üsleri artar , tıpkı kombinatoryal sayıların alt elemanı arttığı gibi.

Bu nedenle, binom teoremini kullanmak için bir kombinatoryal sayının, yani türün cebirsel ifadesinin nasıl çözüleceğini bilmeniz gerekir.

\begin{pmatrix} 4 \\ 2 \end{pmatrix}

. Newton binomunun nasıl hesaplanacağına dair örneklere bakmadan önce, kombinatoryal sayıları kısaca gözden geçirelim.

kombinatoryal sayı

Bir kombinatoryal sayıyı (veya binom katsayısını) belirlemek için aşağıdaki formülü uygulamanız gerekir:

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

Altın

n!

Ve

k!

Bunlar faktöriyel sayılardır . Faktöriyel sayının, 1’in tüm pozitif tam sayılarının bu sayıyla çarpılmasıyla hesaplandığını da hatırlayalım:

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

Örnek olarak, nasıl yapıldığını görebilmeniz için bir kombinatoryal sayı bulacağız:

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

Kombinatoryal sayılar hesap makinesi aracılığıyla da tuşuyla belirlenebilir.

\boxed{nCr}.

Newton Binom Örnekleri

Artık binom teoreminin ne olduğunu bildiğimize göre, iki sayısal örnek kullanarak Newton’un binom formülünü nasıl uygulayacağımızı görelim.

örnek 1

  • Aşağıdaki binomun gücünü hesaplamak için Newton binomunu uygulayın:

(x+3)^2

Açıkçası, bu binomun karesi alındığından, dikkate değer kimlikler için formüllerle de çözülebilir ( dikkate değer kimlikler nasıl çözülür ), ancak bunu örnek olarak binom teoremi ile hesaplayacağız.

Öncelikle Newton’un binom formülünü uygulamalıyız:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

Bu durumda n=2, dolayısıyla:

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

Dikkatli bakın, başlangıçta ilk terimi (x) mümkün olan en yüksek değere, yani bu durumda 2’ye yükseltiyoruz. Öte yandan, ikinci terimi (3) mümkün olan en düşük değere, yani her zaman 0’a yükseltiyoruz. Ama sağa doğru ilerledikçe, ilk terimi öncekinden daha düşük bir sayıya , ikinci terimi ise öncekinden daha yüksek bir sayıya yükseltmemiz gerekiyor.

Şimdi kombinatoryal sayıları hesaplayalım:

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

Güçleri çözüyoruz:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

Son olarak çarpımları hesaplıyoruz:

\left( x+3\right)^2 =x^2 + 6x + 9

Örnek 2

Şimdi biraz daha zor bir problemi çözeceğiz.

  • Aşağıdaki binomun kuvvetini bulmak için Newton’un binom formülünü uygulayın:

(2x+1)^3

Binom teoreminin formülü şöyledir:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

Bu durumda n=3, dolayısıyla:

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

Kombinatoryal sayıları hesaplıyoruz:

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

Şimdi üsleri çözüyoruz, bunun için aşağıdaki iki özelliği hatırlamanız önemlidir:

• Bir tek terimli bir üsse yükseltildiğinde, katsayı ve değişken aynı üsse yükseltilir →

(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• 0’a getirilen herhangi bir terim 1 verir →

(2x)^0=1

Bu nedenle güçleri bu 2 özellik aracılığıyla buluyoruz:

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

Ve son olarak terimleri çarpıyoruz:

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

Newton’un iki terimlisi ve Tartaglia’nın (veya Pascal’ın) üçgeni

Yukarıdaki örneklerde gördüğünüz gibi kombinatoryal sayıları hesaplamak biraz sıkıcıdır. Bu yüzden kombinatoryal sayıları çözmek zorunda kalmamanız için size bir numara öğreteceğiz, çünkü Pascal üçgeni olarak da bilinen Tartaglia üçgenini kullanarak bunların ne kadar değerli olduğunu doğrudan öğrenebilirsiniz.

Ne olduğunu bilmiyorsanız, Pascal üçgeni olarak da adlandırılan Tartaglia üçgeni , üçgen şeklinde düzenlenmiş sayıların matematiksel bir temsilidir.

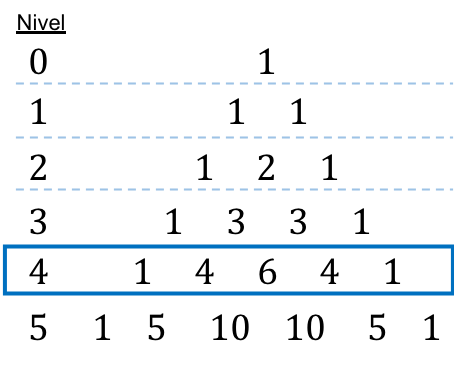
Tartaglia veya Pascal üçgenini oluşturmak için üçgenin her zaman 1 olan tepe noktasından başlamamız gerekiyor ve ardından aşağıdaki çizgilerin numaraları belirleniyor. Aşağıdaki satırlardaki her sayı, her zaman 1 olan satır uçları hariç, hemen üstündeki iki sayının toplamına eşittir.

Newton çifti 1 lise çevrimiçi

Yani Tartaglia üçgenindeki bu sayıların her biri bir kombinatoryal sayının sonucuna karşılık gelir, aşağıdaki şekle bakın:

Örneğin, binom katsayısı

\begin{pmatrix} 3 \\ 1 \end{pmatrix}

3’e eşittir çünkü Tartaglia üçgeninin konumunda 3 vardır.

Bu nedenle Tartaglia (veya Pascal) üçgenini Newton binomunu çok daha hızlı çözmek için kullanabiliriz çünkü bu bizi kombinatoryal sayı hesaplamalarından kurtarır.

Örneğin, bir binomun aşağıdaki potansiyelleştirmesini yapmak istiyorsak:

(x+5)^3

Newton’un binom kuralını uygulayarak aşağıdaki cebirsel ifadeyi elde ederiz:

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

Kombinatoryal sayıları tek tek hesaplamak yerine, her bir kombinatoryal sayıyı Tartaglia üçgeninin karşılık gelen katsayısıyla değiştirebiliriz. Bu durumda binom 3. seviyeye yükseltilir, dolayısıyla üçgenin üçüncü seviyesine karşılık gelir:

Tartaglia veya Pascal üçgeni ve Newton binom

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

Ve şimdi tek yapmamız gereken kalan işlemleri yapmak:

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

Gördüğünüz gibi Tartaglia (veya Pascal) üçgeni, gösterdiğimiz gibi Newton binomunu daha basit ve hızlı bir şekilde hesaplamak için kullanılıyor. Bu yüzden kullanmanızı öneririz.

Şu ana kadar gördüğümüz her şeyi özetlemek için, size Newton binomlarının Tartaglia (veya Pascal) üçgenindeki sayılarla ifadelerinin nasıl göründüğünü gösteren bir resim bırakıyoruz:

Newton binom ve Pascal üçgeni veya Tartaglia

Negatif Newton binom: çıkarma kuvveti

Şu ana kadar Newton binomunun çözdüğümüz tüm örnekleri toplamalardan oluştu. Öte yandan, binomun iki teriminden biri negatif işarete sahip olduğunda prosedür benzer kalır ancak biraz değişir.

Binomun terimlerinden biri negatif olduğunda, yani (ab) n tipinde bir çıkarma olduğunda, Newton binomunun açılımının işaretleri + – + – + – + – … şeklinde değişmelidir.

Aşağıda, ihtiyacınız olan binom ifadesini doğrudan bulabilmeniz için, ilk 5 derecenin negatif binomlarının kuvvetlerini binom teoremi ve Tartaglia üçgeninin katsayıları zaten mevcut olacak şekilde geliştirdik:

bir çıkarma işleminin negatif Newton binom kuvveti 2

Newton binomunun özellikleri

Newton’un binom ifadeleri aşağıdaki özelliklere sahiptir:

  • Newton’un binomunun ayrıştırılması her zaman binomun derecesinden bir terim fazlasıyla sonuçlanır. Veya başka bir deyişle, çift için

    (a+b)^n

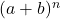
    etkilendiler

    n+1

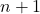
    şartlar.

  • Elementin güçleri

    a

    İle başla

    n

    son çeyrekte 0’a ulaşana kadar azalıyorlar.

  • Elementin güçleri

    b

    diğer yöne giderler: 0’dan başlarlar ve 0’a ulaşana kadar artarlar.

    n

    son dönemde.

  • Newton binomunun her bir elemanı için üslerin toplamı

    a

    Ve

    b

    eşittir

    n.

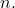
  • Newton’un binom ifadesinin ilk teriminin katsayısı her zaman 1’dir (pozitif), ikinci katsayı ise binomun üssüne (pozitif veya negatif) eşdeğerdir.

Newton binomunun k’inci terimini hesaplayın

Bu alışılmadık bir durum olsa da bazen Newton’un binom açılımını yapmak yerine Newton’un binomunun k’inci terimini, yani k konumunu işgal eden terimi bulmamızın istendiği problemlerle karşılaşabiliriz.

Bu nedenle, Newton binomunda k yerini kaplayan terimi hesaplamak için, binomun toplama mı yoksa çıkarma mı olduğuna bağlı olan bir formül kullanmamız gerekir:

  • Newton binomunun pozitif olması durumunda k’inci terimin değeri aşağıdaki formülle hesaplanır:

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • Newton binomunun negatif olması durumunda k’inci terimin değeri aşağıdaki formülle belirlenir:

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Örnek olarak aşağıdaki 5. derece binomun dördüncü terimini bulacağız:

(x+3)^5

Toplamdan oluşan bir binom olduğundan, ilk formülü uyguluyoruz:

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

Formüldeki değişkenleri karşılık gelen değerleriyle değiştiririz:

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

Ve işlemleri yapıyoruz:

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

Ve bu şekilde Newton’un binom açılımının dördüncü terimini, diğer tüm terimleri hesaplamaya gerek kalmadan hesapladık.

Newton binomuna ilişkin çözülmüş alıştırmalar

Artık binom teoreminin ne olduğunu açıkladığımıza göre, pratik yapabilmeniz için sizi Newton binomuyla ilgili birkaç adım adım çözülmüş alıştırmayla baş başa bırakıyoruz. Ayrıca her türlü soru ve önerinizi bize yorumlarda bırakabileceğinizi unutmayın.

1. Egzersiz

Binom teoremini kullanarak aşağıdaki binom kuvvetini genişletin:

(x+4)^3

İlk önce Newton’un binom formülünü kullanıyoruz:

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

Binom 3’ün kuvvetine yükseltildiğinden, kombinatoryal sayıları doğrudan bulmak için Tartaglia üçgeninin üçüncü seviyesine bakıyoruz:

Newton'un binom teoremi üzerine alıştırmalar adım adım çözüldü lise 1

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

Yetkileri yerine getiriyoruz:

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

Ve son olarak çarpıyoruz:

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

Alıştırma 2

Aşağıdaki gücü Newton’un binom formülüyle hesaplayın:

(3x+2)^3

İlk olarak Newton’un binom formülünü uyguluyoruz:

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

Binomun küpü olduğundan, kombinatoryal sayıların değerlerini doğrudan bilmek için Pascal üçgeninin üçüncü seviyesine bakıyoruz:

Newton'un binom teoremi üzerine alıştırmalar adım adım çözüldü lise 1

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

Monomların kuvvetlerini hesaplıyoruz:

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

Ve son olarak çarpma işlemlerini yapıyoruz:

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

Alıştırma 3

Newton’un binom formülünü kullanarak aşağıdaki polinom ifadesini genişletin:

(2x-2)^3

Öncelikle Newton’un binom formülünü kullanıyoruz. Ancak parantez içinde çıkarma işlemimiz olduğundan, her terimin katsayılarının işaretlerini değiştirmeliyiz:

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

Binom üçün kuvvetine yükseltildiğinden, kombinatoryal sayıları doğrudan hesaplamak için Tartaglia üçgeninin üçüncü seviyesine bakıyoruz:

Newton'un binom teoremi üzerine alıştırmalar adım adım çözüldü lise 1

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

Yetkileri yerine getiriyoruz:

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

Ve çarpmaları çözüyoruz:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

Alıştırma 4

Aşağıdaki Newton binomunun genişletilmiş ifadesini aşağıdaki formülle bulun:

(4x-3y)^4

Newton binomunun genel formülünü uygulamalıyız, ancak bu durumda parantez içinde bir çıkarma işlemimiz olduğundan, her terimin işaretini değiştirmeliyiz:

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

Binom dördüncüye yükseltildiği için, kombinatoryal sayıları doğrudan bulmak için Tartaglia üçgeninin 4. seviyesine bakıyoruz:

Newton'un binom piramidi

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

Tüm güçlerin farkındayız:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

Ve son olarak çarpma işlemlerini çözüyoruz:

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

Alıştırma 5

Aşağıdaki binom ifadesinin açılımındaki yedinci terimi belirleyin:

(2x-5y)^{10}

Negatif bir binom olduğundan aşağıdaki formülü kullanmalıyız:

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

7 terimini belirlemek istiyoruz ve binom 10’un kuvvetine yükseltiliyor, böylece değerleri formülde yerine koyduğumuzda şu hale geliyor:

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

Bu nedenle terimi bilmek için işlem yapmak yeterlidir:

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

Newton binomunun tarihi

Binom teoreminin kökeni ünlü İngiliz bilim adamı Isaac Newton’a (1642-1727) atfedilse de gerçekte teoremin ilk formülasyonu ilk olarak 1000 yıllarında İranlı mühendis Al-Karijí tarafından keşfedilmiştir. 13. yüzyılda Çinli matematikçiler Yang Hui ve Chuh Shih-Chieh küçük dereceli binom açılımlarını zaten biliyorlardı.

Daha sonra, 17. yüzyılda Newton, binom teoremini genişletmek için önceki matematikçilerin attığı temeller üzerine inşa etti. Matematikçi John Walls’un enterpolasyon ve ekstrapolasyon yöntemlerini ve genelleştirilmiş üs kavramlarını kullanarak, bir polinom ifadesini sonsuz bir seriye dönüştürmeyi başardı.

1665 civarında Newton, binom teoremindeki n üssünün aynı zamanda rasyonel bir üs olabileceğini, yani bir binomun kuvvetinin, eğer üs bir kesir ise çözülebileceğini göstermeyi başardı. Öte yandan negatif üs durumunda da bu kanıtlanmıştır. Ve şaşırtıcı bir şekilde, iki ifadenin gelişiminin sonsuz terim dizisi olduğunu keşfetti.

Newton, bu keşifle birlikte sonsuz seriler ile sonlu polinom ifadeleri arasındaki ilişkiyi sorgulamaya başladı ve sonsuz serilerle matematiksel işlemlerin sonlu polinom ifadeleriyle aynı şekilde yapılabileceği sonucunu çıkardı. Newton bu teoremi hiçbir zaman yayınlamamasına rağmen, John Walls sonunda 1685’te bunu yaptı ve bu keşfin Newton’a atfedildiğini belirtti.

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top