▷ Bir sayının faktöriyeli: nedir ve nasıl hesaplanır ✅

Bu sayfada bir sayının faktöriyelinin ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Ayrıca çeşitli örnekler ve en çok kullanılan faktöriyellerin değerlerinin yer aldığı bir tablo sunulmaktadır. Ayrıca hesap makinesiyle bir sayının faktöriyelinin nasıl hesaplanacağını da öğretir. Son olarak faktöriyellerin uygulamaları ve özellikleri anlatılmıştır.

Bir sayının faktöriyeli nedir?

Matematikte bir sayının faktöriyeli , 1’den o sayıya kadar olan tüm pozitif tam sayıların çarpımına eşittir. Ayrıca bir sayının faktöriyeli, sayıdan sonra bir ünlem işareti (!) ile gösterilir.

Örneğin, n sayısının faktöriyelini ( n faktöriyel olarak da bilinir) belirlemek için, n sayısını kendisinden önceki tüm tamsayılarla (birden başlayarak) çarpmanız gerekir:

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

Bir sayının faktöriyeli nasıl hesaplanır

Bir sayının faktöriyelinin anlamını gördükten sonra, bir örnekle herhangi bir faktöriyelin nasıl belirleneceğini görelim:

4’ün faktöriyelini hesaplayın:

Matematiksel tanımında da gördüğümüz gibi bir sayının faktöriyeli, kendisinden küçük veya ona eşit olan tüm pozitif tam sayıların çarpımına eşittir. Bu nedenle 4’ün faktöriyelini hesaplamak için 1, 2, 3 ve 4 sayılarını çarpmamız gerekir:

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

Dolayısıyla 4’ün faktöriyeli 24’ü verir.

Sayıların faktöriyellerine örnekler

Bir sayının faktöriyel kavramını anlamayı tamamlamak için, size farklı sayıların birkaç faktöriyelini hesaplama örneğiyle baş başa bırakıyoruz:

3’ün faktöriyeli:

$3! = 1 \cdot 2 \cdot 3 =6$

5’in faktöriyeli:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

6’nın faktöriyeli:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

1’in faktöriyeli:

$1! = 1$

Mantıksal olarak 1 sayısının faktöriyeli 1’e eşittir çünkü 1’i çarpmak yeterlidir.

0’ın faktöriyeli:

$0! = 1$

Evet, tamam, şaşırtıcı bir şekilde 0’ın faktöriyeli sıfıra değil 1’e eşit. Bu size biraz garip gelebilir çünkü teoride 0’ı 1 ile çarpmanız gerekiyor. Ancak gelenek gereği 0! =1 çünkü ürün özelliği boş . Daha fazla bilgi edinmek isterseniz size bu bağlantıyı bırakıyoruz, sebebini bilmeniz pek önemli olmasa da önemli olan 0’ın faktöriyelinin 1’e eşit olduğunu hatırlamanızdır.

Sayıların faktöriyelleri için sonuçların listesi

Aşağıda en çok kullanılan sayıların faktöriyellerini bir tabloda özetledik, böylece bunları elle hesaplamanıza gerek kalmaz.

Numara	Sayının faktöriyeli
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5.040
8	40.320
9	362.880
on	3.628.800
on bir	39.916.800
12	479.001.600
13	6.227.020.800
14	87 178 291 200
on beş	1.307.674.368.000
16	20.922.789.888.000
17	355.687.428.096.000
18	6.402.373.705.728.000
19	121.645.100.408.832.000
yirmi	2.432.902.008 176.640.000
elli	3.041.409.320 · ^10,64
100	9.332 621.544 · ^10.157
1.000	4.023.872.601 · ^10,2567
10.000	2.846.259.681 · ^10.35.659
100.000	2 824 229 408 · 10 ^{45 6573}
1.000.000	8.263.931.688 · 10 ^5.565.708

Hesap makinesiyle bir sayının faktöriyeli

Önceki örneklerde görüldüğü gibi ardışık iki sayının faktöriyellerinin sonuçları üstel olarak artmaktadır, bu nedenle büyük sayıların faktöriyelini bilmek oldukça zordur. Bu yüzden size hesap makinesiyle bir sayının faktöriyelini nasıl bulacağınızı göstereceğiz.

Bilimsel hesap makinelerinde x sembollü bir anahtar bulunur! veya n! Bir tamsayının faktöriyelini hesaplamak için kullanılır. Dolayısıyla, bir faktöriyelin değerini belirlemek için hesap makinesinde aşağıdaki sırayı uygulamanız gerekir:

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

Normalde CASIO hesap makinelerinde x faktöriyel anahtarı bulunur! veya n! x ^-1 düğmesinin üstünde.

Örnek olarak hesap makinesiyle bir faktöriyel çözeceğiz, böylece nasıl yapılacağını bildiğinizi kontrol edebilirsiniz. Örneğin 9’un faktöriyelini yapacağız:

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

9’un faktöriyelini bulmak için önce 9 sayısını girmeniz, ardından tuşuna basmanız gerekir.

$\boxed{x!}$

ve son olarak eşit düğmesine basın. Bu durumda hesap makinesi bize 362.880 sonucunu göstermelidir.

Faktöriyel numarasının uygulamaları

Bir sayının faktöriyel fonksiyonu çok basit ve saçma bir işlem gibi görünebilir ancak ileri cebirde oldukça fazla kullanılmaktadır. Daha sonra faktöriyelin ana kullanımlarını göreceğiz.

Her şeyden önce, faktöriyel bir kombinatoryal sayının hesaplanması için önemli bir işlemdir, belirli bir işlemden daha fazlasıdır. Kombinatoryal sayının ne olduğunu bilmiyorsanız neyden oluştuğunu ve nasıl hesaplandığını bu linkte görebilir, örnekler, çözümlü alıştırmalar ve özelliklerinin neler olduğunu bulabilirsiniz. Ayrıca gerçek hayatta birçok uygulamaya sahip olduğundan ne için kullanıldığını görebileceksiniz.

Faktöriyel aynı zamanda matematikte bir fonksiyonun Taylor polinomunu belirlemek için de kullanılır.

Benzer şekilde faktöriyel, belirli kombinatoryal problemleri çözmek, özellikle kombinasyonları ve permütasyonları hesaplamak için kullanılır. Bu anlamda, kombinatorik kullanarak olasılıkları hesaplamak için faktöriyeller sıklıkla kullanılır.

N elemanlı bir permütasyon, bu elemanlarla yapılabilecek farklı düzenlemelerin her birine karşılık gelir. Bu nedenle, bir permütasyonu hesaplamak için faktöriyel kullanılır. Örneğin, bir problemde 7 nesnenin düzenlenebileceği olasılıkların sayısını bulmak istiyorsanız, 7’nin faktöriyelini hesaplamanız gerekir.

Şimdi çözülmüş bir alıştırmaya bakalım:

5 farklı ayakkabımız var, bunları kaç farklı şekilde sıralayabiliriz?

Bu alıştırmada, bu 5 çift ayakkabıyı yerleştirdiğimiz sırayı dikkate alarak birleştirmenin tüm olası yollarını keşfetmemiz gerekiyor. Dolayısıyla sorunu çözmek için 5’in faktöriyelini hesaplamanız yeterlidir:

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

Kısaca 5 çift ayakkabı 120 farklı şekilde yerleştirilebiliyor.

Faktöriyel sayısının özellikleri

Faktöriyel numarası aşağıdaki özelliklere sahiptir:

n , m’den büyük olacak şekilde iki pozitif tamsayı n ve m olduğuna göre, bu durumda, açıkçası, n’nin faktöriyelinin değeri, m’nin faktöriyelinin değerinden daha büyüktür.

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

Bir sayının faktöriyeli, faktörlerden biri daha küçük bir sayının faktöriyeli olacak şekilde faktöriyel olarak ayrıştırılabilir.

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> Örneğin 6, 4’ten büyüktür, dolayısıyla 6’nın faktöriyelinin ifadesi şu şekilde basitleştirilebilir: <p class=$ $6! = 6 \cdot 5 \cdot 4!$

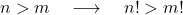
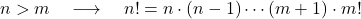
Aşağıdaki cebirsel ifade, 1’in faktöriyeli dışındaki herhangi bir sayının faktöriyeli için geçerlidir:

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

Negatif veya ondalık sayının faktöriyeli

Pozitif bir tam sayının faktöriyelinin değerini nasıl bulacağımızı gördük ama… negatif bir sayının veya ondalık sayının faktöriyelini hesaplayabilir miyiz? Cevap evet ama ileri düzeyde matematik bilgisi gerekiyor.

Negatif bir sayının ve bir ondalık sayının faktöriyeli, Euler’in “Gama fonksiyonu” adı verilen ve aşağıdaki integralle tanımlanan özel bir fonksiyon kullanılarak hesaplanır:

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

Bu nedenle, aşağıdaki denklem her zaman doğru olduğundan, her türlü faktöriyel Gama fonksiyonuyla çözülebilir:

$n! = \Gamma(n+1)$

Yani örneğin 0,5’in faktöriyelini bulmak için değerini bulmalıyız.

$\Gamma(1,5)$

Çünkü:

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

Ve integralin çözümü 0,5’in faktöriyeline karşılık gelecektir.

Açıkçası, Gama fonksiyonunun integralini çözmek kolay değildir ve bunu bu makalede öğretmeyeceğiz çünkü birçok matematiksel kavramın önceden açıklanması gerekecektir. Ancak negatif bir sayının veya ondalık bir sayının faktöriyelini hesaplama imkanının olduğunu bilmenizi istedik.

Aslında örnek olarak bazı negatif faktöriyel ve ondalık değerleri hesapladık:

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$