Cebirsel kesirler: basitleştirme, işlemler, çözülmüş alıştırmalar vb. -

Bu sayfada cebirsel kesirlerin ne olduğunu, ne zaman eşdeğer olduklarını, nasıl sadeleştirileceğini ve cebirsel kesirlerle işlemlerin (toplama, çıkarma, çarpma ve bölme) nasıl yapılacağını açıklıyoruz. Ayrıca cebirsel kesirler için adım adım çözülmüş alıştırmaları görebileceksiniz. Kısacası cebirsel kesirler hakkında herşeyi burada bulacaksınız.

Cebirsel kesirler nelerdir?

Matematikte cebirsel kesir , payında bir polinom ve paydasında başka bir polinom bulunan bir kesirdir.

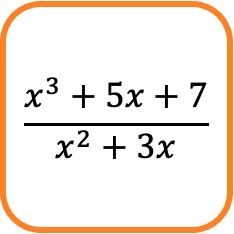
Örneğin yukarıdaki kesirli ifade cebirsel bir kesirden oluşur çünkü pay ve paydası polinomlardan oluşur.

Cebirsel kesir eşdeğeri

Cebirsel kesirlerin tanımını öğrendikten sonra, bu tür iki kesrin ne zaman eşit olduğunu görelim.

Matematiksel olarak, aşağıdaki koşul karşılanırsa iki cebirsel kesir eşdeğerdir :

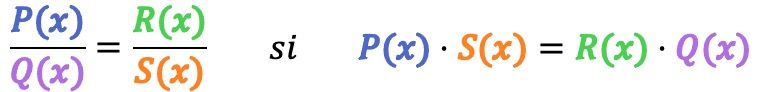
Örnek olarak aşağıdaki 2 cebirsel kesrin eşdeğer olup olmadığını kontrol edeceğiz:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Kesirlerin cebirsel olarak eşit olup olmadığını belirlemek için terimlerini enine çarparız:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Şimdi polinomların çarpımlarını hesaplayalım:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Denklemin her iki tarafında da aynı ifadeyi elde ettik, yani bunlar fiilen iki eşdeğer cebirsel kesirdir.

Cebirsel kesirleri basitleştirin

Cebirsel bir kesri basitleştirmek için önce pay ve paydadaki polinomları çarpanlara ayırmanız, ardından ortak çarpanları ortadan kaldırmanız gerekir.

Açıkçası cebirsel kesirleri basitleştirmek için polinom çarpanlarına ayırmanın ne olduğunu ve nasıl yapıldığını bilmeniz önemlidir. Eğer hala polinomların nasıl çarpanlara ayrıldığını bilmiyorsanız veya tam olarak hatırlamıyorsanız, devam etmeden önce bağlantılı sayfaya gitmenizi tavsiye ederim, aksi halde prosedürü zar zor anlayabilirsiniz. Polinomların çarpanlarına nasıl ayrılacağını adım adım açıklıyor ve ayrıca çeşitli örnekleri görebileceksiniz ve çözülmüş alıştırmalarla pratik yapabileceksiniz.

Şimdi bir örnek kullanarak polinomları çarpanlara ayırma yöntemini uygulayarak cebirsel bir kesirin nasıl basitleştirildiğini görelim:

Aşağıdaki cebirsel kesri sadeleştirin:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Öncelikle kesrin pay ve paydasının polinomlarını çarpanlarına ayırıyoruz:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Polinomların nasıl çarpanlara ayrıldığını bilmiyorsanız yukarıdaki bağlantıya bir göz atın)⬆

Polinomları çarpanlarına ayırdıktan sonra pay ve payda arasındaki ortak çarpanları ortadan kaldırıyoruz, yani tekrarlanan tüm terimleri kaldırıyoruz:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

Basitleştirilmiş cebirsel kesir bu nedenle şuna benzer:

$\cfrac{(x+1)(x+2)}{x-1}$

Bu problemde cebirsel kesirin polinomları kökleri bulunarak çarpanlara ayrıldı; ancak bazen bir polinom ortak çarpanı alınarak doğrudan çarpanlara ayrılabilir (çok daha hızlı yöntem). Bu bağlantıda bir polinomdan ortak çarpan almanın ne anlama geldiğini göreceksiniz ve ortak çarpanı kullanarak cebirsel bir kesri nasıl basitleştireceğinizi keşfedeceksiniz.

Cebirsel kesirlerle işlemler

Her kesir türünde olduğu gibi cebirsel kesirlerle de işlemler yapılabilir. Spesifik olarak cebirsel kesirler toplanabilir, çıkarılabilir, çarpılabilir ve bölünebilir. Aşağıda her bir işlem türünün nasıl hesaplandığını örneklerle adım adım açıklıyoruz.

Cebirsel kesirleri toplama ve çıkarma

Cebirsel kesirleri toplama ve çıkarma prosedürü pratik olarak aynıdır, bu yüzden onları birlikte analiz edeceğiz. İlk önce iki cebirsel kesirin eklenmesine ilişkin bir örnek göreceğiz ve aşağıda cebirsel kesirlerin çıkarılması yöntemi arasındaki farkı inceleyeceğiz.

Cebirsel kesirleri toplama

Cebirsel kesirlerin eklenmesi normal kesirlerle aynı şekilde yapılır: önce kesirleri ortak bir paydaya indirgeyin, sonra payları ekleyin.

Bir örnek kullanarak cebirsel kesirlerin nasıl toplandığını görelim:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Öncelikle kesirlerin paydalarını çarpanlarına ayırıyoruz:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Şimdi kesirleri ortak bir paydaya indirgemek için paydaların lcm’sini (en küçük ortak kat) bulmamız gerekiyor.

İpucu: Paydaların lcm’si her zaman ortak olan faktörlerin çarpımından en büyük üsse kadar ortak olmayan faktörlerle çarpılarak oluşturulur.

Örneğin bizim durumumuzda

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

En büyük üsse yükseltilmiş paydalar arasındaki ortak bölen:

$(x+1)^2.$

Paydalar arasındaki ortak olmayan faktör ise

$x.$

Dolayısıyla bu durumda paydaların lcm’si şöyledir:

$(x+1)^2 \cdot x$

Bu nedenle paydaların lcm’si

$(x+1)^2 \cdot x,$

dolayısıyla bu 2 kesrin yeni paydası olacaktır.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Ortak paydayı bulduktan sonra payları değiştirmeliyiz. Bunu yapmak için normal kesirlerin eklenmesiyle aynı işlemi izliyoruz: her kesir için lcm’yi bölüyoruz

$\bigl( \ x(x+1)^2 \ \bigr)$

orijinal payda arasında ve sonucu payla çarpın:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Şimdi paydaları aynı olduğundan iki kesri bir araya getirebiliriz:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Son olarak pay üzerinde işlem yapıyoruz. İlk önce tek terimli ve polinomun çarpımını yaparız:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Daha sonra benzer terimleri paya ekliyoruz:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Normalde zaten orada olurduk ama bu soruna yakından bakarsak paydan ortak bir çarpanı çıkararak cebirsel kesri daha da basitleştirebiliriz. Henüz:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

Ve böylece iki cebirsel kesrin toplamını zaten tamamladık.

Cebirsel kesirlerin çıkarılması

Cebirsel kesirleri çıkarmak için, cebirsel kesirleri toplamaya benzer bir prosedür izlemeliyiz: önce kesirleri ortak bir paydaya indirgeyin, sonra payları çıkarın.

Bir örnekle cebirsel kesirlerin nasıl çıkarıldığını görelim:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Öncelikle iki kesrin paydalarını çarpanlarına ayırmamız gerekiyor:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Normal kesirlerin çıkarılmasında olduğu gibi, kesirleri ortak bir paydaya indirgemek için şimdi paydaların lcm’sini (en küçük ortak kat) hesaplamamız gerekir. Bu durumda paydaların lcm’si;

$(x+2)^2(x-3) ,$

dolayısıyla bu 2 kesrin yeni paydası olacaktır.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Şimdi normal kesirleri çıkarmak için uyguladığımız işlemin aynısını uyguluyoruz: her kesir için lcm’yi bölüyoruz

$\bigl( \ x(x+1)^2 \ \bigr)$

orijinal payda arasında ve sonucu payla çarpın:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Şimdi paydaları aynı olduğundan iki cebirsel kesri birleştiriyoruz:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

Ve pay üzerinde işlem yapıyoruz. İlk önce polinom çarpımlarını çözüyoruz:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Cebirsel kesirlerde çıkarma işleminde çok sık yapılan bir hata, çarpma işlemini yaptıktan sonra parantez koymayı unutmaktır. Negatif işaret yalnızca ilk terimi değil, çarpımın sonuçta ortaya çıkan tüm öğelerini etkilediğinden bu bir hata olacaktır.

Parantez içindeki işlemleri yapıyoruz:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Böylece negatif işaret sayesinde parantez içindeki tüm terimlerin işaretini değiştiriyoruz:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

Ve son olarak benzer tek terimlileri gruplandırıyoruz:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Cebirsel kesirlerin çarpımı

Cebirsel kesirleri çarpmak için önce söz konusu kesirlerin tüm polinomlarını çarpanlara ayırıyoruz, sonra payları birbirleriyle, paydaları birbirleriyle çarpıyoruz ve son olarak elde edilen kesri sadeleştiriyoruz.

Bu nedenle cebirsel kesirlerin çarpımı aslında normal kesirlerin çarpımı ile aynı şekilde hesaplanır.

Şimdi bir örnekle iki cebirsel kesrin nasıl çarpılacağını görelim:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Öncelikle kesirlerin tüm polinomlarını, hem pay hem de paydalarını çarpanlarına ayırmanız gerekir:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Şimdi kesirleri çarpalım. Bunu yapmak için pay ve paydaları birlikte çarpıyoruz:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

Son olarak payda ve payda tekrarlanan çarpanları basitleştiriyoruz:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Buna göre çarpmanın sonucu:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

Kesir daha fazla basitleştirilemez. Yani cebirsel kesirleri çarpmayı zaten bitirdik.

Cebirsel kesirlerin bölünmesi

Cebirsel kesirlerin bir bölümünü hesaplamak için, önce tüm polinomları çarpanlara ayırırız, sonra kesirleri enine çarparız (birinci pay ikinci paydayla ve birinci payda ikinci payla) ve son olarak cebirsel kesri basitleştiririz.

Bir örnek kullanarak iki cebirsel kesrin nasıl bölündüğünü daha iyi görelim:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

İki cebirsel kesri bölmenin ilk adımı, işlemde yer alan tüm polinomları çarpanlarına ayırmaktır:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Şimdi kesirleri bölmemiz gerekiyor. Bunun için kesirleri enine çarpıyoruz yani birinci pay ikinci payda ile çarpılır ve sonuç yeni kesrin payı olur ve aynı şekilde birinci payda ikinci pay ile çarpılır. ve sonuç yeni kesrin paydası olacaktır:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Payda ve payda tekrarlanan faktörleri basitleştiriyoruz:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

Kesiri daha da basitleştirebiliriz, çünkü

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

Kesir daha fazla basitleştirilemez. Bu nedenle cebirsel kesirleri zaten böldük.

Cebirsel kesirler üzerine çözülmüş alıştırmalar

Aşağıda size cebirsel kesirler konusunda adım adım çözülmüş birkaç alıştırma sunuyoruz, böylece pratik yapabilir ve böylece kavramı anlamayı tamamlayabilirsiniz. Aklınıza takılan tüm soruları bize yorumlarda sorabileceğinizi unutmayın! 💬💬💬

1. Egzersiz

Aşağıdaki cebirsel kesirlerin eşdeğer olup olmadığını belirleyin:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Çözümü görün

İki cebirsel kesrin eşdeğer olup olmadığını kontrol etmek için bunları enine çarpmanız ve eşitlik elde edip etmediğinize bakmanız gerekir. Bu yüzden ilk önce birinci ve ikinci kesri kontrol edeceğiz:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Denklemin solundaki dikkate değer özdeşliği çözüyoruz:

$x^2-9=x^2-9$

✅

Bu durumda bir eşitlik elde ettik, yani birinci ve ikinci kesirler cebirsel olarak eşittir.

Şimdi aynı prosedürü birinci ve üçüncü cebirsel kesirlere uyguluyoruz:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Ancak bu sefer cebirsel kesirler denklemi sağlamadığından birinci ve üçüncü kesirler matematiksel olarak farklıdır.

Sonuç olarak, üçüncü kesir birinci kesirden farklıdır ve dolayısıyla birinci ve ikinci kesirler eşdeğer olduğundan ikinci kesre de eşit değildir.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Alıştırma 2

Aşağıdaki cebirsel kesirleri basitleştirin:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Çözümü görün

Cebirsel bir kesri basitleştirmek için pay ve paydadaki polinomları çarpanlara ayırmamız, sonra tekrarlanan çarpanları elememiz gerekir. Henüz:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Alıştırma 3

Cebirsel kesirlerin aşağıdaki toplama ve çıkarma işlemlerini hesaplayın:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Çözümü görün

Cebirsel kesirleri eklemek (veya çıkarmak) için önce kesirleri ortak bir paydaya indirgemeli, sonra payları eklemeli (veya çıkarmalıyız). BU YÜZDEN:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Alıştırma 4

Cebirsel kesirlerin aşağıdaki çarpma ve bölme işlemlerini çözün:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Çözümü görün

Cebirsel kesirleri çarpmak için önce tüm polinomları çarpanlara ayırmamız, ardından pay ve paydaları çarpmamız ve son olarak elde edilen kesri basitleştirmemiz gerekir.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Öte yandan, cebirsel kesirleri bölmek için önce tüm polinomları çarpanlara ayırırız, sonra kesirleri enine çarparız (birinci pay ikinci paydayla ve birinci payda ikinci payla) ve son olarak bulunan cebirsel kesri basitleştiririz.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Açıklama hakkında ne düşünüyorsunuz? Hoşuna gitti mi? Veya herhangi bir öneriniz var mı? 💬 Yorumlarda bu sayfa hakkında ne düşündüğünüzü bize bildirin! Hepinizi okuyoruz! 👀 Ayrıca tüm sorularınızı bize sorabileceğinizi de unutmayın! ❔👇❔👇

Cebirsel kesirler: sadeleştirme, işlemler, çözümlü alıştırmalar,…

Cebirsel kesirler nelerdir?

Cebirsel kesir eşdeğeri

Cebirsel kesirleri basitleştirin

Cebirsel kesirlerle işlemler

Cebirsel kesirleri toplama ve çıkarma

Cebirsel kesirleri toplama

Cebirsel kesirlerin çıkarılması

Cebirsel kesirlerin çarpımı

Cebirsel kesirlerin bölünmesi

Cebirsel kesirler üzerine çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et