Bu sayfada bir polinomun ortak faktörünün nasıl alınacağını (veya çıkarılacağını) açıklıyoruz. Burada farklı ortak faktör türlerini bulacaksınız ve bunun nasıl başarıldığına dair birkaç örnek görebileceksiniz. Ayrıca adım adım çözülen egzersizlerle antrenman yapabilirsiniz.
Ortak faktör nedir?
Matematikte ortak faktör , bir polinomun tüm terimlerinde bulunan bir faktördür; yani ortak faktör, bir polinomun her terimini çarpan bir sayı veya harften oluşur.
Örnek olarak aşağıdaki polinomun ortak faktörünün ne olduğunu tanımlayacağız:
![]()
4 numarada polinomun tüm terimlerinde tekrarlanır:
![]()
Dolayısıyla bu polinomun ortak çarpanı 4’e eşittir.
![]()
Ortak çarpan nasıl elde edilir (veya çıkarılır)
Ortak faktörün anlamını öğrendikten sonra, bir polinomdan ortak faktörün nasıl elde edileceğine bakalım.
Bir polinomun iki veya daha fazla teriminin ortak bir çarpanı varsa, polinomun toplama veya çıkarma işlemlerini bir çarpmaya dönüştürmek için ortak faktör alınabilir (veya çıkarılabilir) .
Bunu yazmak biraz zor görünebilir, bu yüzden bir örnekle bir polinomdan ortak faktörü nasıl çıkaracağımızı görelim:
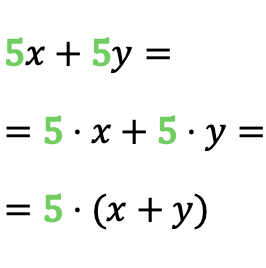
Örnekte gördüğünüz gibi 5 sayısı tek terimli 5x’te ve tek terimli 5y’de tekrarlanıyor, yani polinomun ortak çarpanı 5’tir. Yani ortak çarpanı belirledikten sonra tek terimlilerin toplamını bir sayıya dönüştürebiliriz. ürün.
Ortak çarpanı çıkarırken parantez içine almayı unutmayın çünkü ortak çarpanın tüm toplananları çarpması gerekir.
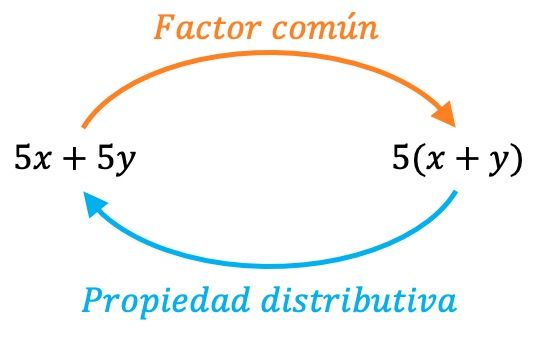
Ortak çarpanı kaldırmak, dağılma özelliğinin ters işlemidir, yani aslında dağılma özelliğini tersten uyguluyoruz. Bu nedenle, ters işlemi gerçekleştirerek ortak çarpanı doğru şekilde çıkardığımızı her zaman doğrulayabiliriz:
- Dağılma özelliğini uygulayarak aynı polinomu baştan elde ediyorsak bu, ortak faktörü doğru bir şekilde elde ettiğimiz anlamına gelir.
- Öte yandan, dağılma özelliğinin kullanılması sonucu orijinal polinomdan farklı başka bir polinom çıkması, ortak çarpanı çıkarma işleminde hata yaptığımızı gösterir.
Ortak Faktör Alma (veya Çıkarma) Örnekleri
Ortak faktör kavramını anlamanızı tamamlamak için size daha fazla örnek bırakıyoruz:
örnek 1
Bu örnekte gördüğünüz gibi, ikiden fazla terimden aynı anda ortak bir çarpan çıkarılabilir:
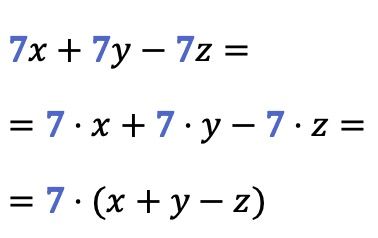
Örnek 2
Ayrıca değişkenlerden (veya harflerden) ortak bir faktör çıkarabilirsiniz:
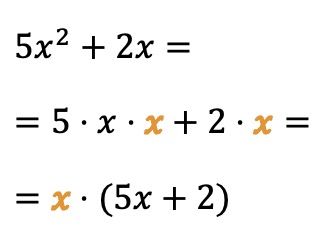
Bu durumda x harfi polinomun iki terimini çarpar, dolayısıyla x değişkenini ortak çarpan olarak alarak cebirsel ifadeyi basitleştirebiliriz.
Örnek 3
Bu örnekte, ilk terimde x değişkeni 3’ün kuvvetine yükseltilmiştir ve ikinci terimde x’in kuvveti 2’ye yükseltilmiştir, dolayısıyla her iki terimde de iki x bulunur. Dolayısıyla ortak çarpan sadece x değil, x 2’dir :
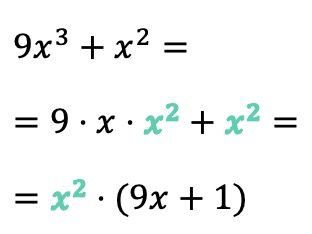
Öte yandan, polinomun ortak çarpanı bir terimle tam olarak çakışıyorsa, ortak çarpanı çıkarırken yerine 1 koymamız gerektiğine dikkat edin . Aksi takdirde yerine herhangi bir şey koymasaydık eşdeğer bir ifade elde edemezdik.

Örnek 4
Bazen ortak çarpan o kadar belirgin değildir ve doğrudan görülmez, daha ziyade tek terimlilerin katsayılarının bir böleni olabilir. Örneğin, 6 ve 9’un faktöriyel ayrışımı 3 içerdiğinden aşağıdaki örnekteki ortak faktör 3’tür:
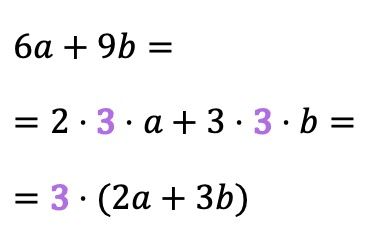
Bu tür ortak faktöre bazı cebir kitaplarında maksimum ortak faktör adı verilir, çünkü ortak faktör aynı zamanda polinom terimlerinin katsayılarının en büyük ortak faktörüdür (GCD).
Buraya kadar geldiyseniz, bu muhtemelen bir polinomun ortak faktörünü nasıl bulacağınızı zaten bildiğiniz anlamına gelir; mükemmel. Ancak ortak faktörün ne işe yaradığını hiç merak etmediniz mi? Ortak çarpanın bir uygulaması da polinomları çarpanlara ayırmak için kullanılmasıdır. Hala ne olduğunu bilmiyorsanız, bu bağlantıda polinom çarpanlara ayırmanın ne olduğunu ve bu polinom işlemini gerçekleştirmek için ortak faktörün neden bu kadar önemli olduğunu görebilirsiniz.
Kesirler için ortak faktör
Ortak faktör aynı zamanda pay ve paydada polinomlar bulunan terimleri kesirlere basitleştirmek için de çok kullanışlıdır.
Bunun nasıl yapıldığını görmek için aşağıdaki kesri örnek olarak basitleştirelim:
![]()
Yapmamız gereken ilk şey pay polinomu ile payda polinomunun ortak faktörünü bulmaktır. Bu durumda iki polinomun ortak çarpanı 2’dir:
![]()
Şimdi iki polinomun ortak faktörünü çıkaralım:
![]()
Her iki polinom için ortak bir faktör elde ettikten sonra pay ve paydada tekrar eden faktörleri çıkarmamız gerekir :
![]()
Sonuç olarak basitleştirilmiş kesir şu şekildedir:
![]()
Gruplandırmaya göre ortak faktör
Bir polinomun terimlerini azaltmanın bir yolu, aynı zamanda çift ortak faktör çıkarma olarak da adlandırılan terimleri gruplandırarak ortak faktör yöntemini kullanmaktır. Adından da anlaşılacağı gibi bu prosedür, bir polinomun ifadesinin, terimlerini iki kez gruplandırarak basitleştirilmesinden oluşur.
Bu yöntem biraz karmaşık olduğundan, aşağıdaki polinomla adım adım nasıl uygulandığını görelim:
![]()
Öncelikle iki farklı olası ortak faktörü belirlememiz gerekiyor, bu nedenle polinomu iki parçaya ayırıyoruz:
![]()
Bu durumda, x 2 ve 2x elemanlarının ortak çarpanı x harfine, 5x ve 10 terimlerinin ortak çarpanı ise 5’e sahiptir (çünkü 10, 5’in katıdır). Yani şu iki ortak noktamız var:
![]()
![]()
Ve son olarak, kalan iki polinom çarpımı (x+2) faktörüne sahip olduğundan, polinomu aşağıdaki şekilde basitleştirebiliriz:
![]()
Gördüğünüz gibi bu yöntem hiç de kolay değil. Bu nedenle aklınıza takılan soruları bize yorum kısmından sormaktan çekinmeyin, en kısa sürede cevaplayacağız.
Ortak faktörler alıştırmaları adım adım çözüldü
Bir polinomdan ortak çarpanı çıkarma konusunda pratik yapabilmeniz için size adım adım çözülmüş birkaç alıştırma bırakıyoruz.
1. Egzersiz
Aşağıdaki polinomlardan ortak faktörü çıkarın:
![]()
![]()
![]()
![]()
A) İlk polinomu oluşturan tüm terimler 6’ya sahiptir, dolayısıyla polinomun ortak çarpanı 6’dır:
![]()
B) İkinci polinomun tüm elemanlarında en az bir x harfi vardır. Polinomun ortak çarpanı şu şekildedir:
![]()
C) Polinomun ilk tek terimlisinin 2 olduğu ve ikinci tek terimlinin de 2’nin katı olduğu açıktır. Yani polinomun ortak çarpanı 2’dir:
![]()
D) Son polinomda tüm değişkenlerin en az kareleri alınır. Dolayısıyla ortak çarpan x 2’dir :
![]()
Ortak çarpan bir terimle aynı olduğunda yerine 1 konulması gerektiğini unutmayın.
Alıştırma 2
Aşağıdaki polinomların ortak faktörünü düşünün:
![]()
![]()
![]()
![]()
A) Birinci polinomu oluşturan elemanların tüm katsayıları 2’nin katıdır, dolayısıyla ortak çarpan çıkarıldığında polinom şu şekilde olur:
![Rendered by QuickLaTeX.com \begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7862ee57cf098358e43d3b669e0cb54d_l3.png)
B) Polinomun tüm terimlerinde en az bir x vardır, dolayısıyla:
![Rendered by QuickLaTeX.com \begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39551a1ffc0b98f8b9c037fdcc793b01_l3.png)
C) Polinomun tüm terimlerinin katsayılarının en büyük ortak böleni 5’tir, dolayısıyla adı geçen polinomun ortak böleni 5’tir:
![Rendered by QuickLaTeX.com \begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fe8cc019c3511734ff278f68c44066df_l3.png)
D) Polinomdaki tüm terimler en az bir x’e sahiptir ve üstelik tüm katsayılar 3’ün katıdır. Dolayısıyla polinomun ortak faktörü 3x’tir:
![Rendered by QuickLaTeX.com \begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fb70701f39b1050eec730f1591671293_l3.png)
Alıştırma 3
Aşağıdaki polinomların her birinin ortak faktörünü bulun ve çıkarın:
![]()
![]()
![]()
![]()
A) Tüm tek terimlilerde en az harf bulunur
![]()
karesi ve harfi
![]()
küp olduğuna göre ortak çarpan
![]()
![Rendered by QuickLaTeX.com \begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b622844f35f4bd4411c545c352331943_l3.png)
B) Polinomun tüm katsayıları 8’in katıdır ve ayrıca değişmez kısımlar olarak en az x 2 ve y 2’ye sahiptirler. Dolayısıyla polinomun ortak faktörü 8x 2 y 2’dir .
![Rendered by QuickLaTeX.com \begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2d7018f427d800f6db67335a4d4f238b_l3.png)
C) Bu durumda ortak faktör ara monomiyalin değeriyle çakışır
![]()
diğer monomların katsayıları katları olduğundan
![]()
ve kesinlikle herkes var
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76f91563726822a51c7bfe88aa461e6d_l3.png)
D) Bu özel durumda polinomun tüm terimlerinde hiçbir faktör tekrarlanmadığından polinomun ortak çarpanı yoktur. Bu nedenle polinom ifadesi cebirsel olarak basitleştirilemez.
![]()
Alıştırma 4
Aşağıdaki cebirsel kesirleri ortak çarpanı alarak basitleştirin:
![]()
![]()
![]()
![]()
Cebirsel bir kesri, yani polinomlu bir kesri basitleştirme prosedürü, kesrin pay ve paydasından ortak faktörü çıkarmak, ardından yukarıda ve aşağıda tekrar eden faktörleri ortadan kaldırmaktır. fraksiyonun altındadır. BU YÜZDEN:
![Rendered by QuickLaTeX.com \text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ce28a7207aa3bccea5a8afae54c8ad5_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a6024cf2af6c13d0d27f7e5d3e675362_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5678b7c6d631a693a86fad40aa79d030_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82199184b3594c18db6888c58fa0bdfc_l3.png)
Alıştırma 5
Aşağıdaki polinom ifadelerinin ortak faktörünü alın:
![]()
![]()
![]()
![]()
A) Polinomun tüm terimleri faktöriyel olarak üçüncüye ayrıştırılabilir, dolayısıyla:
![Rendered by QuickLaTeX.com \begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66174ecc5c7264ae95507f632d1f2630_l3.png)
B) Polinomun kök içindeki ortak faktörü 4’tür, ancak o zaman ortak faktörün karekökünü hesaplayarak çıktısını alabiliriz:
![Rendered by QuickLaTeX.com \begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a362644fe5b22fefc962f164db26f5e_l3.png)
C) Bu polinomda ortak faktörün çıkarılması işlemini gruplandırarak uygulayabiliriz:
![Rendered by QuickLaTeX.com \begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd43d5f40797c39b0401769ff392d9e5_l3.png)
D) Polinomun tüm kesirli katsayıları yarının katı olduğundan polinomun ortak faktörü ½’dir.
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a35ab3db2e1f1197d6652e6d4d0a8a8a_l3.png)
👇👇👇 Açıklama hakkında ne düşündünüz? Hoşuna gitti mi? Ayrıca unutmayın, bir polinomun ortak faktörünün nasıl belirlendiğine dair sorularınız varsa veya bir alıştırmayı anlamadıysanız, bize her zaman yorumlarda sorabilirsiniz, biz de size cevap vereceğiz. 👇👇👇