Bu sayfada polinomları bölmek için Ruffini kuralının nasıl uygulanacağını açıklıyoruz. Açıklamaya ek olarak polinomların Ruffini kuralıyla bölünmesine ilişkin adım adım çözülmüş örnekleri ve alıştırmaları görebileceksiniz. Ayrıca bu yöntemin tüm uygulamalarını bulacaksınız ve aslında birden fazlası sizi kesinlikle şaşırtacaktır.
Ruffini kuralı nedir?
Matematikte Ruffini kuralı, herhangi bir polinomu xr biçimindeki polinomlara hızlı bir şekilde bölmenize olanak tanıyan cebirsel bir yöntemdir. Ruffini kuralı, adını bu yöntemi icat eden matematikçi Paolo Ruffini’den almıştır.
Ancak Ruffini kuralı yalnızca polinomları bölmek için kullanılmaz, başka birçok kullanım alanı vardır. Örneğin, Ruffini kuralı aynı zamanda bir polinomun köklerini bulmak, bir polinomun sayısal değerini bulmak, bir polinomu çarpanlara ayırmak ve hatta üçüncü derece veya daha yüksek denklemleri çözmek için de kullanılır. Aşağıda tüm bu işlemleri gerçekleştirebilmek için Ruffini kuralının nasıl uygulandığını göreceğiz.
Son olarak, Ruffini kuralı aynı zamanda Ruffini yöntemi, Ruffini teoremi veya polinomların sentetik bölümü olarak da bilinir.
Ruffini kuralı nasıl uygulanır?
Gördüğümüz gibi, Ruffini kuralının ana kullanımı bir polinomu bir binomla bölmektir, yani aşağıdaki türden bir bölme işlemi yapmaktır:
![]()
Ruffini kuralını kullanmak için, bölen polinomun her zaman bir x (katsayısı 1’e eşit) ve bir sayıdan (pozitif veya negatif) oluşması gerektiğini unutmayın; aksi takdirde Ruffini algoritması kullanılamaz.
Ruffini kuralını uygulamak için tam bir prosedür izlenmelidir; bu nedenle aşağıda Ruffini kuralının (veya Ruffini yönteminin) nasıl uygulandığını görmek için adım adım bir örnek çözeceğiz.
Ruffini kuralına örnek
- Aşağıdaki polinom bölümünü Ruffini kuralını kullanarak çözün:
![]()
Öncelikle birbiriyle kesişen iki dik çizgi çizmeniz, ardından böleni ve böleni aşağıdaki gibi yerleştirmeniz gerekir:
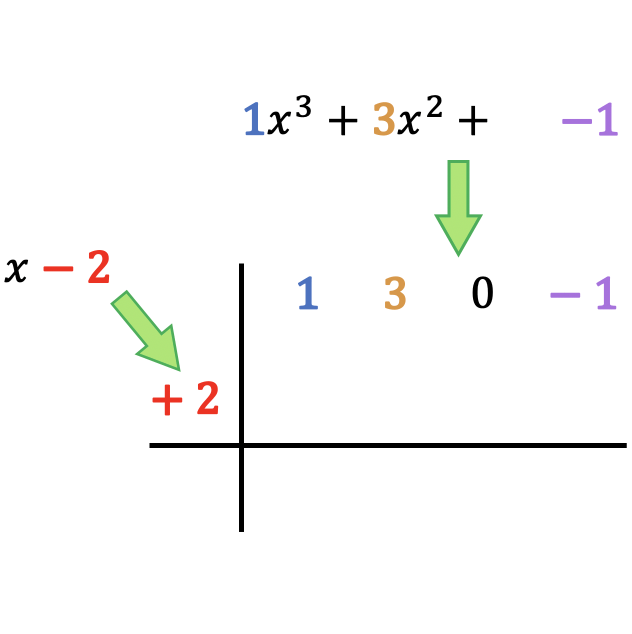
Gördüğünüz gibi, bölen polinomunun katsayılarını en yüksek dereceden en düşüğe doğru sıralayarak en üste koymamız gerekiyor ve bölen polinomunun bağımsız terimini işaret değişikliği ile kutunun soluna yerleştirmeliyiz.
Uyarı: Bölünme polinomunun belirli derecede bir terimi yoksa (eksik polinom), yerine 0 konur. Örneğin, bu durumda polinom
![]()
1. derece monomiye sahip olmadığı için yerine 0 koyduk.
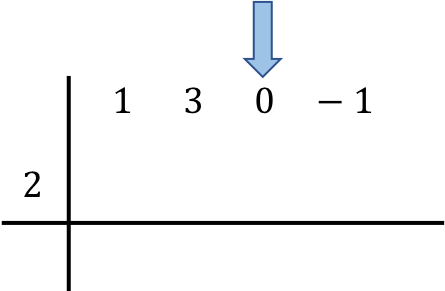
İşlemde yer alan polinomları konumlandırdıktan sonra ilk sayıyı doğrudan aşağıdaki satıra indiriyoruz:
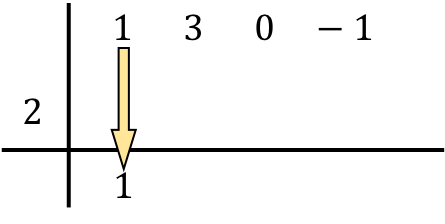
Şimdi Ruffini kuralını karakterize eden adım geliyor: Aşağıdaki sayıyı soldaki sayıyla çarpıyoruz ve sonucu aşağıdaki sütuna yerleştiriyoruz :
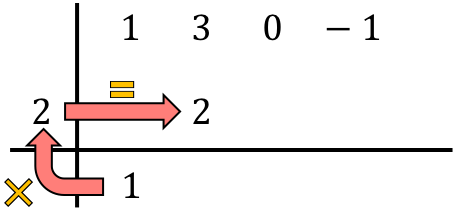
Ve sütundaki sayıları toplayarak toplamın sonucunu hemen altına koyuyoruz:
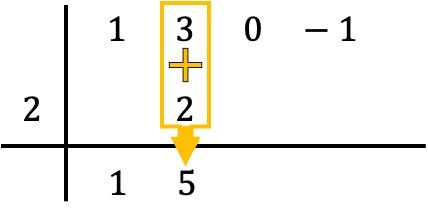
Yani Ruffini’nin yöntemi bu sürecin tekrarlanmasını içeriyor. Böylece aynı şeyi tekrar yapıyoruz: alttaki sayıyı soldaki sayıyla çarpıyoruz, sonucu bir sonraki sütuna koyuyoruz ve son olarak dikey olarak hizalanan sayıları topluyoruz:
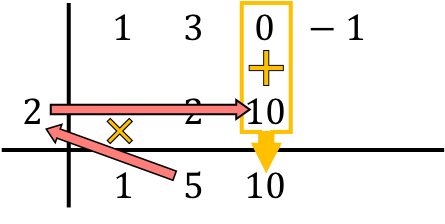
Ve aynı işlemi sonuna kadar art arda tekrarlıyoruz. Önce aşağıdaki sayının soldaki sayıyla çarpımını yapıyoruz, sonra sonucu bir sonraki sütuna yerleştiriyoruz ve son olarak aynı sütundaki sayıları topluyoruz:
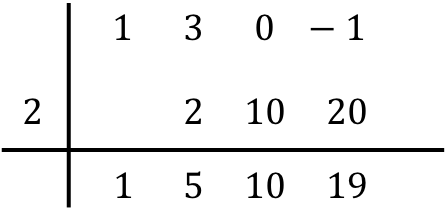
Yani tüm sütunları doldurduğumuzda polinomları bölmeyi bitirmiş oluyoruz.
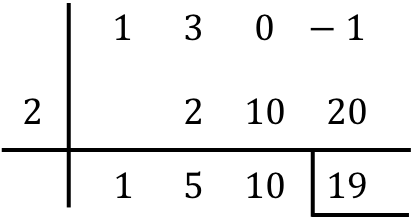
Yani polinomları bölmenin sonucunu bulmanız yeterli:
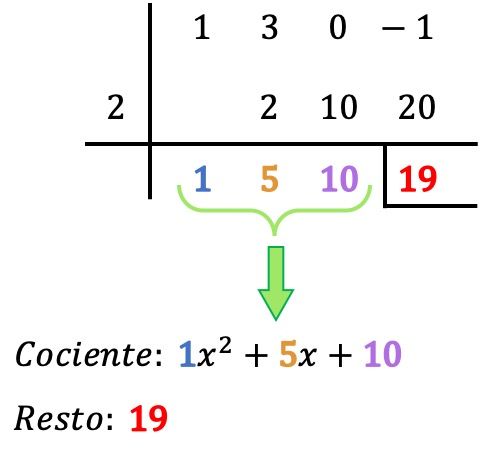
- İki polinom arasındaki bölümün geri kalanı aşağıdaki satırdaki son sayıdır, dolayısıyla bizim durumumuzda geri kalan 19’a eşittir. Geri kalan genellikle sola bir çubuk ve adı geçen sayının altına bir çubuk yerleştirilerek gösterilir.
- Polinom bölümünün bölümü , polinom bölümünün katsayıları olan elde edilen diğer değerlerle belirlenir. Sağdan ilk rakam 0.sınıf dönemin katsayısına karşılık gelir, sonraki rakam 1.sınıf dönemin katsayısına karşılık gelir, sonraki rakam 2.sınıfın, sonraki hane 3.sınıfın katsayısıdır… ve sonuna kadar böyle devam eder. . BU YÜZDEN:
Ruffini kuralının çözülmüş alıştırmaları
Aşağıda Ruffini kuralıyla ilgili birkaç adım adım çözülmüş alıştırma bulacaksınız, böylece bu yöntemle polinomların bölümlerini nasıl çözeceğinizi pratik edebilir ve anlayabilirsiniz. Her egzersizi denemenizi ve ardından düzeltmeye bakarak doğru yapıp yapmadığınızı kontrol etmenizi öneririz.
1. Egzersiz
Aşağıdaki polinom bölme işlemini Ruffini kuralıyla gerçekleştirin:
![]()
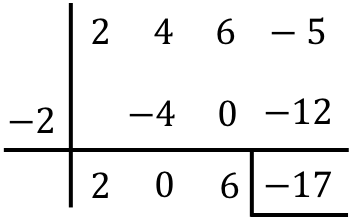
Dolayısıyla iki polinom arasındaki bölümün sonucu:
Bölüm:
![]()
Dinlenmek:
![]()
Alıştırma 2
Ruffini kuralını kullanarak aşağıdaki polinom bölümünü hesaplayın:
![]()
Bu özel durumda, bölüştürme polinomunun ikinci dereceden bir terimi yoktur, dolayısıyla onun yerine sıfır koymalıyız:
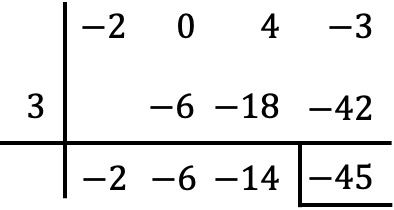
Bu nedenle 2 polinom arasındaki bölümün sonucu şu şekildedir:
Bölüm:
![]()
Dinlenmek:
![]()
Alıştırma 3
Aşağıdaki polinomların Ruffini kuralına göre bölünmesinin sonucunu bulun:
![]()
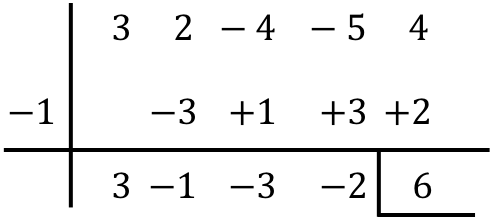
Sonuç olarak, iki polinomu bölmenin sonucu:
Bölüm:
![]()
Dinlenmek:
![]()
Alıştırma 4
Aşağıdaki polinom bölümünden kalanın 5’e eşit olmasını sağlayacak şekilde bilinmeyen m’nin değerini bulun:
![]()
Bölen (xr) veya (x+r) biçiminde olduğundan, bölmeyi çözmek için Ruffini kuralını uygulayabiliriz. Bu nedenle bilinmeyen m’yi sürükleyerek Ruffini’nin yöntemini uyguluyoruz:
Şimdi elde edilen kalanı 5’e eşitliyoruz çünkü kalanın 5 olması gerekiyor:
![]()
Ve m parametresinin değerini bulmak için denklemi çözüyoruz:
![]()
![]()
Yani m değişkeni 3’e eşit olduğunda polinomlar arasındaki bölümün geri kalanı 5’e eşit olacaktır.
Alıştırma 5
Aşağıdaki polinom bölümünün geri kalanını 3 verecek şekilde m parametresinin değerini belirleyin:
![]()
Bölen (xr) veya (x+r) biçiminde olduğundan, bölmeyi çözmek için Ruffini kuralını uygulayabiliriz. Bu nedenle bilinmeyen m’yi sürükleyerek Ruffini’nin yöntemini kullanıyoruz:
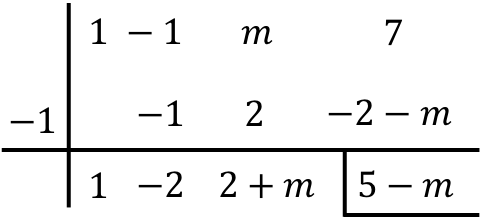
Son çarpma sırasında dağılma özelliğini aklınızda bulundurun:
![]()
Öte yandan bölmenin geri kalanının hesaplanması şu şekildedir:
![]()
![]()
![]()
Bölmenin geri kalanının 3’e eşit olması gerektiğinden, şimdi elde edilen kalan ifadesini 3’e eşitliyoruz:
![]()
Ve m parametresinin değerini belirlemek için ortaya çıkan denklemi çözüyoruz:
![]()
![]()
![]()
![]()
Bu nedenle polinom bölümünün geri kalanının 3’e eşit olması için m’nin 2’ye eşit olması gerekir.
Ruffini kuralının daha fazla uygulaması
Açıklandığı gibi, Ruffini kuralı esas olarak polinomlar arasındaki bölmeyi gerçekleştirmek için kullanılır. Ancak Ruffini kuralı diğer hesaplamaları yapmak için de kullanılır; bunların her birini aşağıda göreceğiz.
Bir polinomun kökleri
Bir polinomun kökleri Ruffini kuralı kullanılarak kolayca belirlenebilir. Bir polinomun kökünün ne olduğunu bilmiyorsanız tanımını gözden geçirelim:
Bir polinomun kökleri (veya sıfırları), polinomu iptal eden değerlerdir. Veya başka bir deyişle, bir polinomun kökleri, polinomda değerlendirildiğinde sayısal değeri 0’a eşit olan değerlerin tamamıdır.
![]()
Öte yandan, kalan teoremi sayesinde biliyoruz ki, belirli bir değer için bir polinomun sayısal değeri
![]()
sıfırdır, zorunlu olarak söz konusu polinomun aşağıdakiler arasındaki bölümünden kalan kısımdır:
![]()
Ayrıca 0 olması gerekir.
![]()
Bu nedenle, bir polinomu bölmek için Ruffini kuralını kullanırsanız
![]()
formun başka bir polinomu arasında
![]()
0’a eşit bir kalan elde ederiz, bu şu anlama gelir:
![]()
polinomun bir köküdür
![]()
Bir örnekle elbette daha iyi anlayacağız:
- Kontrol eğer
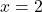
polinomun bir köküdür
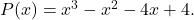
Verilen değerin polinomun kökü olup olmadığını kontrol etmek için, Ruffini yöntemini adı geçen polinom ve adı geçen değerle uygulamanız yeterlidir:
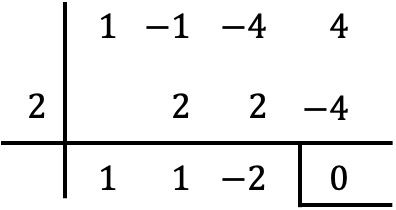
Ruffini kuralıyla elde edilen kalan sıfıra eşit olduğundan, bu şu anlama gelir:
![]()
polinomun bir köküdür
![]()
Polinomları çarpanlara ayırma
Ruffini kuralı genellikle faktöriyel polinomlara uygulanan yöntemdir, çünkü derece 3, 4, 5 vb. bir polinomun tüm köklerini hızlı bir şekilde bilmenizi sağlar.
Şimdi bir örnek kullanarak Ruffini algoritmasıyla bir polinomu nasıl çarpanlara ayıracağımızı görelim:
- Aşağıdaki üçüncü derece polinomu çarpanlarına ayırın:
![]()
Yapılacak ilk şey polinomun tüm köklerini bulmaktır. Ve bir polinomun olası kökleri, bu durumda 6 olan bağımsız terimin bölenleridir. Yani:
Polinomun olası kökleri: +1, -1, +2, -2, +3, -3, +6, -6
Şimdi polinomu bu değerlerin her biri arasında Ruffini kuralıyla bölmeye çalışmamız gerekiyor. Bölmenin geri kalanı 0 ise bu, değerin polinomun kökü olduğu anlamına gelir; ancak bölümün geri kalanı 0 değilse değer polinomun kökü değildir. Bu nedenle, Ruffini kuralını tüm sayılarla test etmek yalnızca aşağıdaki üç durumda kalanları iptal eder:
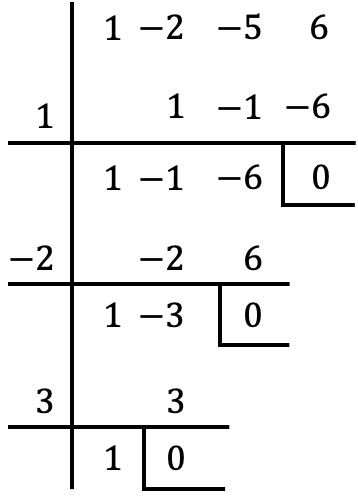
Dolayısıyla problemdeki polinomun kökleri, kalanın sıfırlandığı değerlerdir, yani:
![]()
Son olarak polinomu çarpanlarına ayırmak için her kökü ifade etmemiz gerekir.
![]()
tipin bir faktörü şeklinde
![]()
yani her kök için bir parantez koymanız gerektiği anlamına gelir
![]()
ve bulunan kökün işareti değişti:
![]()
Gördüğünüz gibi Ruffini kuralını kullanarak polinomu başarıyla çarpanlarına ayırdık. Ancak çok karmaşık bir konu olduğu için polinomları çarpanlara ayırma konusunda şüpheleriniz olmuş olabilir. Bu durumda polinomların nasıl çarpanlara ayrılacağı ile ilgili makalemizi web sitemizde (sağ üstteki arama motorunda) arayabilirsiniz , orada bunu daha ayrıntılı olarak açıklıyoruz ve onunla adım adım çözülmüş alıştırmalar yapabilirsiniz. Ayrıca polinomları çarpanlara ayırmanın başka yöntemlerini de gösteriyoruz.
Bir polinomun sayısal değerini hesaplayın
Şaşırtıcı görünse de, bir polinomun sayısal değeri, kalan teoremini kullanan Ruffini kuralıyla belirlenebilir.
Ancak bunu yapabilmek için kalan teoremini bilmeniz gerektiği açıktır. Eğer durum böyle değilse kalan teoreminin açıklamasını web sitemizde (sağ üstteki arama motorunda) arayabilirsiniz .
Yani kalan teoremi sayesinde herhangi bir polinomun sayısal değerini bilebiliriz. Bir örnek kullanarak bunun nasıl yapılacağını görelim:
- Sayısal değerini hesaplayın

İçin
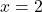
Ruffini kuralını uygulayarak,
![]()
Değere ait polinomun sayısal değerini bulmak için
![]()
Yapmamız gereken tek şey Ruffini kuralını polinom ve söz konusu değerle kullanmaktır:
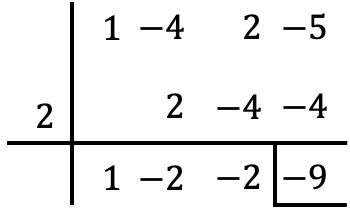
Böylece kalan teoreminden polinomun sayısal değerinin polinom bölümünün geri kalanıyla çakıştığını biliyoruz. Bu nedenle polinomun sayısal değeri
![]()
-9’dur.
![]()
Öte yandan sayısal değeri sayısal olarak hesaplayarak Ruffini kuralının doğru uygulandığını doğrulayabiliriz:
![Rendered by QuickLaTeX.com \begin{aligned} P(2) &= 2^3-4\cdot 2^2+2\cdot 2-5\\[2ex] &= 8-4\cdot 4+2\cdot 2-5 \\[2ex] & = 8-16+4-5 \\[2ex] & =\bm{-9} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c935b3276a3915dbdf93755851ef28e5_l3.png)
Üçüncü derece veya daha yüksek denklemleri çözün
Ruffini kuralının bir başka uygulaması da derecesi 2’den büyük denklemlerin çözülmesidir, çünkü bu durumlarda ikinci derece denklemdeki gibi bir formül yoktur. Bir örnek kullanarak bunun nasıl yapılacağını görelim:
- Aşağıdaki ikinci dereceden denklemi Ruffini kuralını kullanarak çözün:
![]()
Denklemi bir polinommuş gibi ele almamız gerekiyor. Daha sonra, ikinci dereceden bir denklem elde edene kadar Ruffini kuralını kullanarak “polinomun” mümkün olduğu kadar kökünü hesaplamalıyız . Bu durumda bu 3. dereceden bir denklemdir, dolayısıyla “polinomun” bir kökünü belirlemek yeterlidir:
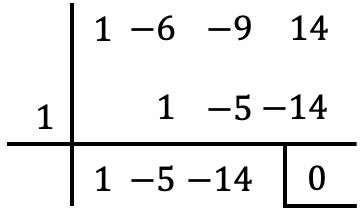
Bu nedenle denklemin bir çözümü şöyle olacaktır:
![]()
Diğer çözümleri bulmak için Ruffini kuralı bölümünden elde edilen polinomu 0’a eşitlemeliyiz:
![]()
Ve şimdi ortaya çıkan ikinci dereceden denklemi karşılık gelen formülüyle çözüyoruz:
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x = \cfrac{5 \pm 9}{2} = \begin{cases} \cfrac{5+9}{2} = \cfrac{14}{2} = 7 \\[4ex]\cfrac{5-9}{2} = \cfrac{-4}{2} = -2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a57aa9f04a1053566c6a53b65afa008a_l3.png)
Sonuç olarak, üçüncü derece denklemin 3 çözümü şunlardır:
![]()