▷ Kalan teoremi: nedir, örnekler ve çözülmüş alıştırmalar ✅

Burada kalan teoreminin (veya kalan teoreminin) ne olduğunun ve polinomlara nasıl uygulandığının açıklamasını bulacaksınız. Ayrıca örnekleri görebilecek ve ayrıca kalan teoremi üzerinde adım adım çözülmüş alıştırmalar yapabileceksiniz.

Kalan teoremi nedir?

Matematikte, kalan teoremi , herhangi bir P(x) polinomunun (xa) formundaki başka bir polinomla bölümünden kalanın, x=a değeri için P(x) polinomunun sayısal değerine eşit olduğunu söyler. başka bir deyişle, P(x):(xa) bölümünün geri kalanı P(a)’ya eşdeğerdir.

Kalan teoremi örneği

Kalan teoreminin ne olduğunu gördükten sonra, bunun pratik bir uygulamasına bakalım:

Aşağıdaki iki polinom arasındaki bölümün kalanını hesaplayın:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

Polinom bölümünün geri kalanını (veya kalıntısını) bulmak için kalan teoreminden yararlanabiliriz, çünkü bu durumda bölme polinomu (xa) formundadır, yani birinci dereceden katsayıdır. x değişkeni 1’dir ve bağımsız bir terime sahiptir.

Bu nedenle, böyle bir bölme işleminin geri kalanının, işareti değiştirilmiş bölen polinomunun bağımsız teriminde değerlendirilen bölen polinomunun sayısal değerine eşit olduğunu söyleyen kalan teoremini uyguluyoruz, yani P(1).

Bu nedenle bölümün geri kalanını bulmak için x=1’deki polinomu değerlendirmemiz gerekir:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

Bu nedenle polinomlar arasındaki bölümün geri kalanı 2’dir .

Öte yandan, Ruffini’nin polinomları bölme kuralını kullanarak kalanın bulduğumuz sonuçla örtüştüğünü de kontrol edebiliriz:

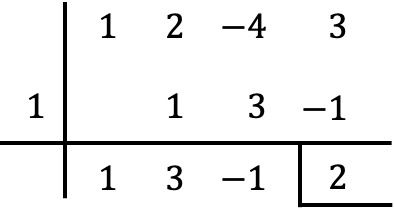
Gördüğünüz gibi, bir polinomun binomla bölünmesinin kalanını kalan teoremi ile belirlemek, Ruffini kuralına göre çok daha hızlı ve kolaydır, çünkü çok daha az hesaplama yapılır.

Kalan ve faktör teoremi

Kalan teoreminden ve bir polinomun kökünün (veya sıfırının) tanımından faktör teoremini çıkarabiliriz. Dolayısıyla faktör teoremi aşağıdakileri ifade eder:

Faktör teoremi , bir P(x) polinomunun (xa) formundaki başka bir polinomla ancak ve ancak P(a)=0 olması durumunda bölünebileceğini söyler. Ve bu durumda bu, a’nın P(x) polinomunun bir kökü veya sıfır olduğu anlamına gelir.

Ayrıca, kalan teoremine göre bu, eğer bir polinom başka bir polinoma bölünebiliyorsa, P(a)=0 olduğundan söz konusu bölümün geri kalanının sıfır olacağı anlamına gelir.

Örneğin, belirli bir polinomumuz varsa:

$P(x)=x^2+2x-8$

Bu polinom binom (x-2) ile bölünebilir çünkü P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

x=2, P(x) polinomunu iptal ettiğinden, bu, x=2’nin adı geçen polinomun bir kökü olduğu anlamına gelir.

Ayrıca P(2)=0 olduğundan, kalan teoremi sayesinde bölümün geri kalanının ne olduğunu biliyoruz.

$\cfrac{x^2+2x-8}{x-2}$

0’a eşittir.

Kalan teoreminin çözülmüş alıştırmaları

Kalan teoremini anlamayı tamamlamak için, pratik yapabilmeniz amacıyla adım adım çözülen bazı alıştırmalar hazırladık. Egzersizi önce kendiniz denemenizi ve ardından doğru yapıp yapmadığınızı kontrol etmenizi öneririz.

1. Egzersiz

Kalan teoremine göre polinom bölümünün geri kalanını bulun

$\cfrac{P(x)}{Q(x)}$

, işlemde yer alan polinomlar olmak üzere:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

Çözümü görün

Bölen polinomu yalnızca birinci dereceden bir terim ve bir bağımsız terimden oluşur ve üstelik birinci dereceden terimin katsayısı 1’dir. Dolayısıyla kalan teoremini kullanabiliriz.

Kalan teoremini uygulamak için de, bölen polinomun işareti değişen bağımsız terimindeki bölen polinomunu değerlendirmek yeterlidir, yani P(2)’yi hesaplamak gerekir.

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

Dolayısıyla iki polinom arasındaki bölümün geri kalanı 21’dir .

Alıştırma 2

Polinom göz önüne alındığında

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

Elde edilen kalanı aşağıdaki polinomların her birine bölerek bulun:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

Çözümü görün

Bölen polinomların tümü kalan teoreminin koşullarını karşıladığından, her bölümün kalanını belirlemek için bu teoremi kullanabiliriz:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

Alıştırma 3

Parametrenin değerinin ne kadar olması gerektiğini hesaplayın

$m$

böylece polinomların bölümünden kalan kısım

$\cfrac{P(x)}{Q(x)}$

her ikisi de polinom olduğundan 3’e eşit olacaktır:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

Çözümü görün

Bu özel durumda, bölen polinom birinci dereceden bir monom ve bağımsız bir terimden oluşur ve ayrıca birinci dereceden monomiyalin katsayısı 1’dir. Bu nedenle kalan teoremini kullanabiliriz.

Kalan teoremini kullanmak için, bölünen polinomun bağımsız terimini, bölünmüş polinomda bir x’in olduğu yerde bir işaret değişikliği ile değiştirin, dolayısıyla P(-3)’ü çözmemiz gerekir.

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$

Ama açıkçası bilinmeyene dayalı bir sonuç elde ediyoruz

$m.$

Ancak problem ifadesi bize kalanın üçe eşit olması gerektiğini söylüyor, dolayısıyla bulunan kalanı 3’e eşitlememiz gerekiyor:

$3m-63 = 3$

Ve son olarak denklemi çözüyoruz:

$3m = 3+63$

$3m = 66$

$m = \cfrac{66}{3}$

$\bm{m = 22}$

Alıştırma 4

Polinomun olup olmadığını faktör ve kalan teoremi ile belirleyin

$P(x)$

polinom ile bölünebilir

$Q(x).$

$P(x) =-2x^3-5x^2-x+2 \qquad \qquad Q(x)=x+2$

Çözümü görün

Böylece polinom

$P(x)$

polinomla bölünebilir olmak

$Q(x)$

bu iki polinom arasındaki bölüm tam olmalı ve bu nedenle kalan sıfır olmalıdır.

O zaman bölen polinomu olduğundan

$(x+2),$

Faktör teoremi ve kalan teoreminden biliyoruz ki polinom

$P(x)$

polinomla bölünebilir

$Q(x)$

eğer doldurulursa

$P(-2)=0.$

Bu nedenle bu eşitliğin doğrulanıp doğrulanmadığını görmemiz gerekir:

$P(-2)=0 \quad \color{blue} \bm{?}$

$\begin{aligned} P(-2) &=-2\cdot (-2)^3-5\cdot (-2)^2-(-2)+2\\[2ex] &=-2 \cdot (-8) -5 \cdot 4+2 +2\\[2ex] & =16-20+2+2 \\[2ex] & =0\end{aligned}$

Aslında bölümün geri kalanı

$\cfrac{P(x)}{Q(x)}$

0’a eşittir, dolayısıyla polinom

$P(x)$

Evet diğer polinoma bölünebilir

$Q(x).$

Açıklama hakkında ne düşünüyorsunuz? Hoşuna gitti mi? Umalım ki öyle olsun! Önerilerinizi veya sorularınızı bize yorumlarda bırakabileceğinizi unutmayın. ⬇⬇⬇Hepinizi okuyoruz! 😁😁

Kalan (veya kalıntı) teoremi