Polinom bölümü

Bu sayfada polinomları nasıl böleceğinizi, hem bir polinomun bir tek terime bölünmesini, hem de bir polinomun başka bir polinom tarafından bölünmesini öğreneceksiniz. Ayrıca polinomları bölme örneklerini görebilecek ve adım adım çözülmüş alıştırmalarla pratik yapabileceksiniz. Ayrıca bu polinom işleminin özelliklerini de bulacaksınız.

Polinom (veya polinom) bölümü

İki polinomun tam olarak nasıl bölündüğünü görmeden önce polinom bölmesi kavramlarını kısaca gözden geçireceğiz, böylece kullanacağımız yöntemi anlamak daha kolay olacaktır.

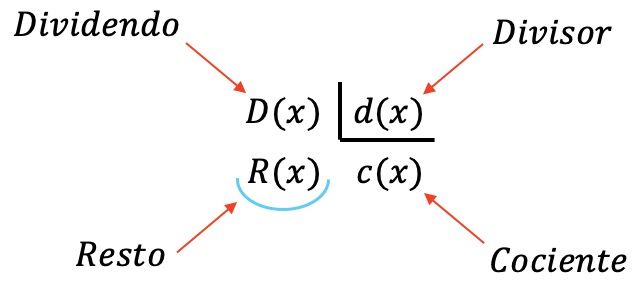
Bir polinom bölümünde dört polinom yer alır:

• Bölünme : bölünmüş polinom.
• Bölen : Bölen polinom.
• Bölüm : Temettüyü bölene bölmenin sonucu.
• Kalan (veya kalıntı): iki polinom arasında bölündüğünde kalan polinom.

Öte yandan polinomlar arasında iki tür bölme olduğunu da bilmelisiniz:

• Polinomların tam bölünmesi : Polinomlar arasındaki bölme, kalan sıfır olduğunda tamdır. Bu durumda polinom böleni, bölenin bölümle çarpımına eşittir.

Ayrıca bu durumda temettü

bölenin katıdır

ve bölüm

Benzer şekilde, polinom böleni ve polinom bölümünün her ikisi de bölenin bölenleridir.

• Polinomların tamsayı bölümü : polinomların tamsayı (veya tam olmayan) bölümünde kalan sıfırdan farklıdır (0). O halde polinom bölümünün temel özelliği sağlanır:

Artık polinomları bölmenin ne olduğunu gördüğümüze göre, polinomları birbirine nasıl böleceğimize bakalım. Daha doğrusu, önce bir polinom ile bir monom arasındaki bölmeyi, ardından 2 polinom arasındaki bölmeyi açıklayacağız.

Bir polinomun bir tek terime bölünmesi

Bir polinomun bir monoma nasıl bölündüğünü görmeden önce, öncelikle monomların kendi aralarında nasıl bölündüğünü hatırlayalım, çünkü bu tip polinom işlemlerini yapabilmek için bunu bilmek gerekir.

İki monomlu bölme işlemi, katsayılarının birbirine ve gerçek kısımlarının birbirine bölünmesini içerir, yani monomların katsayıları bölünür ve aynı tabana sahip değişkenlerin üsleri çıkarılır. Aşağıdaki örneğe bakın:

Şimdi bir polinomun bir tek terime bölünmesinin neleri içerdiğini görelim:

Matematikte, bir polinomun bir tek terime bölünmesini çözmek için, polinomun her terimi tek terime bölünür.

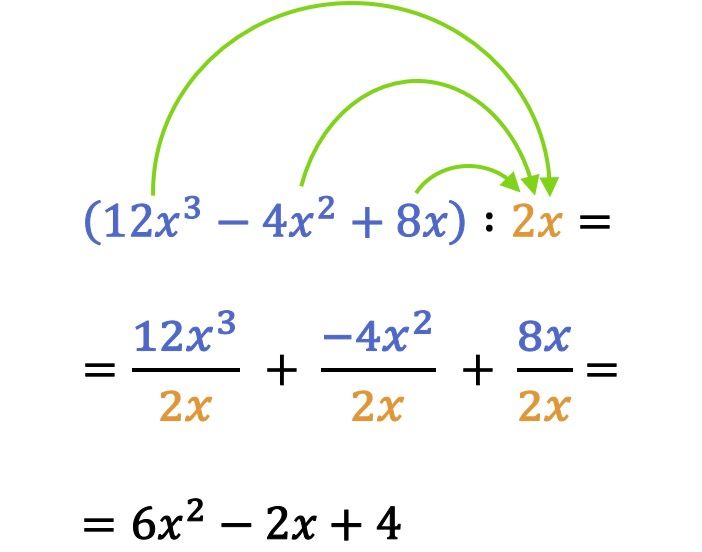
Önceki bölme örneğinde, tek terimlileri veya polinomları bölerken işaret kuralını da dikkate almanız gerektiğine dikkat edin. Aslında polinomlar ve monomiyaller arasındaki bölme işleminde çok yaygın bir hata, bir terimin işaretini yanlış anlamaktır.

Bir polinomun başka bir polinom tarafından bölünmesi

İki polinomu bölmek için bir prosedür izlemeniz gerekir; o halde, bir örneği adım adım çözerek, polinomların uzun bölümü olarak da adlandırılan polinomları bölme yönteminin nasıl göründüğüne bakalım:

• Polinomu bölmenin sonucunu hesaplayın

  

  polinom arasında

  

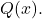
  İki polinom olmak üzere:

Yapılacak ilk şey polinomları bölme formuna koymaktır. Sol tarafa kesrin payını (bölen polinomu) yazıyoruz ve sağ tarafa kesrin paydasını (bölen polinomu) yazıyoruz:

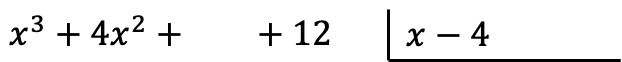
Uyarı: Eğer bir polinomun belli derecede monomiyeli yoksa yerine boşluk bırakmalıyız. Örneğin polinom

Birinci yıl dönemi yoktur, dolayısıyla onun yerine boş bir alan vardır.

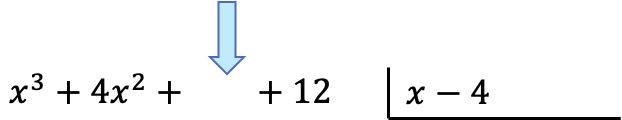
Polinomları yerleştirdikten sonra bölümü bulacağız. Bölümün ilk terimini bulmak için, bölenin ilk terimini bölenin ilk terimine bölmemiz gerekir:

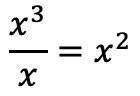
Ve bölümün sonucunu bölümün yerine koyarız:

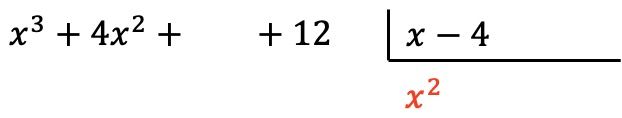
Şimdi bölenin her bir elemanı tarafından bulunan terimi çarpıyoruz ve her sonucu , işaretini değiştirerek ilgili sütundaki bölenin altına koyuyoruz:

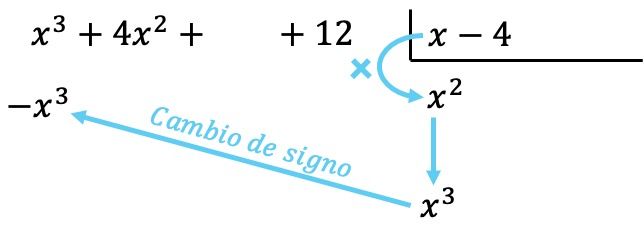
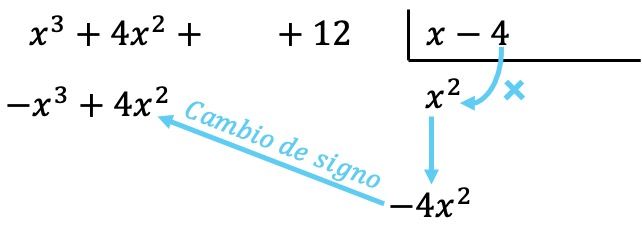
Polinomlarla yapılan tüm işlemlerde olduğu gibi, aynı dereceden tüm terimlerin aynı sütunda olması için polinomların en yüksek dereceden en düşük dereceye doğru sıralanması önemlidir.

Çarpma sonuçlarını ters işaretle yerleştirdikten sonra dikey olarak hizalanmış terimleri eklememiz gerekir:

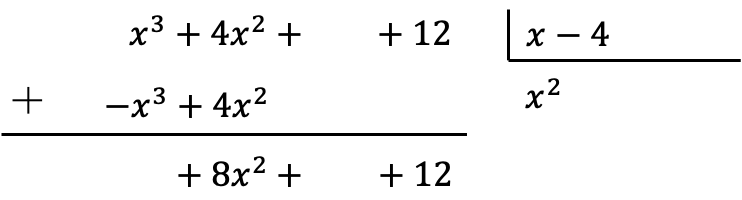
Bu toplamı yaptığımızda, en yüksek dereceye sahip katsayının birbirini götürdüğünü ve dolayısıyla temettüde bir dönem eksik kaldığımızı unutmayın.

Şimdi polinom böleni polinom bölenden bir derece az olana kadar aynı işlemi tekrarlamamız gerekiyor.

Bu nedenle temettünün ilk terimini bölenin ilk terimine bölüyoruz:

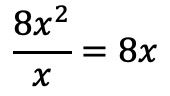
Sonucu bölüme yerleştiririz:

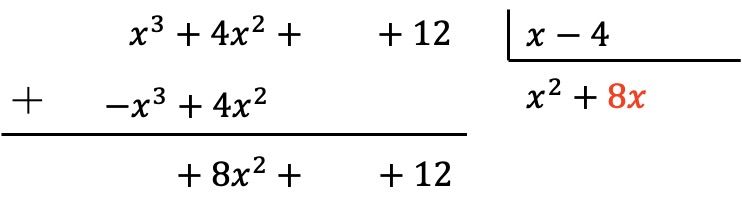
Daha önce olduğu gibi, bölümün yeni terimini bölenin her bir elemanıyla çarpıyoruz ve zıt işaretli sonuçları bölenin ilgili sütunlarına yerleştiriyoruz:

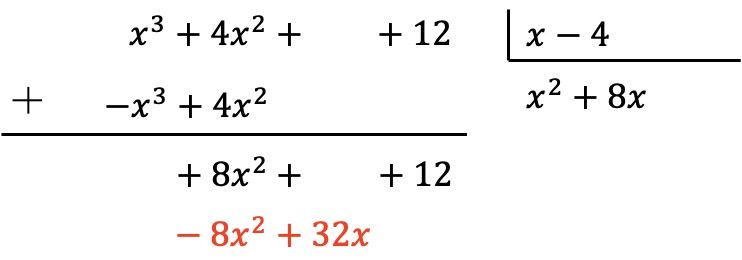
Ve dikey olarak ekliyoruz:

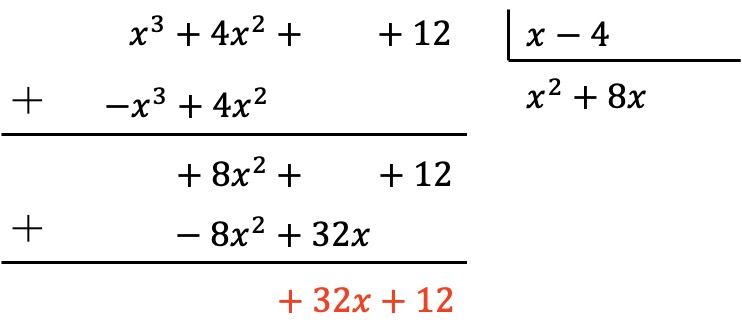
Bölünme polinomu hala bölen polinomundan bir derece eksik değil, bu yüzden aynı işlemi yapmaya devam etmemiz gerekiyor.

Yani önce bölenin ilk terimini bölenin ilk terimine böleriz, sonra sonucu bölenin her terimiyle çarparız, sonra değiştirilen sonuçları bölenin işaretine koyarız ve son olarak dikey olarak ekleriz:

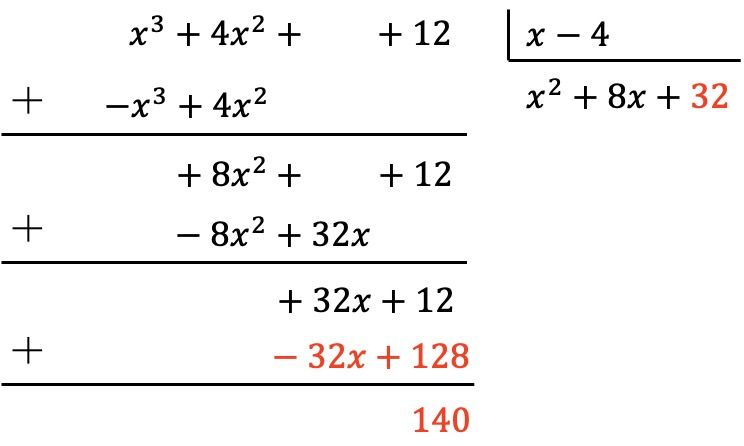
Böylece, bölenin polinomunun derecesinin bölenin derecesinden küçük olduğunu zaten elde ettik, çünkü bölen 0. dereceden ve bölen de 1. derecedendir. Bu nedenle bölme tamamlandı.

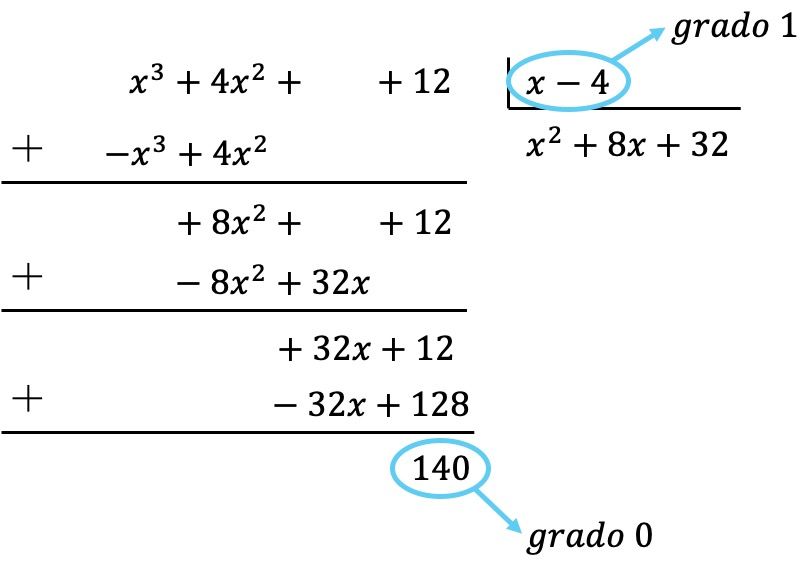
Buna göre bölme işleminin sonucu:

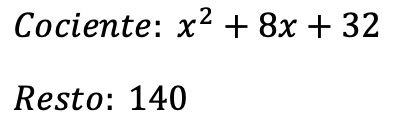
Öte yandan polinomların bölünmesinin temel koşuluna dayanarak polinom bölmesini doğru bir şekilde yaptığımızı doğrulayabiliriz:

✅

Denklem sağlandı, dolayısıyla polinom bölümü doğru bir şekilde gerçekleştirildi.

Polinomları bölmeyi bitirdiğimize göre, bu açıklamada size yardımcı olabildiğimizi umuyoruz. Polinomları bölme yöntemi hakkında ne düşünüyorsunuz? Bir şüphen mi var? Hoşuna gitti mi? Yoksa polinom bölümlerinin var olmamasını mı tercih edersiniz? 😂 Sizi yorumlarda okuyoruz! 👇👇👇

Polinomları bölmenin özellikleri

Polinomların herhangi bir bölümü aşağıdaki özellikleri karşılar:

✓ Polinom böleninin derecesi her zaman polinom bölenin derecesinden büyük olmalıdır.

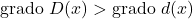✓ Polinom böleninin derecesi, bölenin ve bölümün derecelerinin toplamına eşittir.

✓ Kalanın derecesi her zaman bölenin (ve dolayısıyla bölenin) derecesinden küçüktür.

✓ Temettü, bölenin çarpımı ile bölüm artı kalanının çarpımına eşittir. Bu koşul sayıların bölünmesinde de konur.

Polinomların bölünmesine ilişkin çözülmüş alıştırmalar

1. Egzersiz

Bir polinomun bir tek terime bölünmesinin aşağıdaki sonucunu belirleyin:

Bir polinomu bir tek terime bölmek için, polinomun her teriminin söz konusu tek terime bölünmesini çözmeniz gerekir:

Tek terimli sayılar arasında bölme yaparken katsayıların kendi aralarında bölündüğünü ve tabanı aynı olan kuvvetlerin üslerinin çıkarıldığını unutmayın.

Alıştırma 2

Bir polinomun bir tek terime aşağıdaki bölümünü hesaplayın:

Bir polinomu bir tek terime bölmek için, polinomun her terimini söz konusu tek terime bölmeniz gerekir:

Tek terimli bölme işleminde katsayıların kendi aralarında bölündüğünü ve eşdeğer tabanlı kuvvetlerin üslerinin çıkarıldığını unutmayın.

Alıştırma 3

Bir polinomun bir tek terime bölünmesini aşağıdaki şekilde çözün:

Bir polinomu bir tek terime bölmek için, polinomun her teriminin söz konusu tek terime bölünmesini çözmeniz gerekir:

Bölen tek terimlinin negatif olduğunu ve bu nedenle tüm bölümlerin işaretlerinin değiştiğini unutmayın.

Alıştırma 4

Polinomların aşağıdaki bölünmesini gerçekleştirin:

Polinomları bölmek için yukarıda açıklanan yöntemi uygulamanız gerekir:

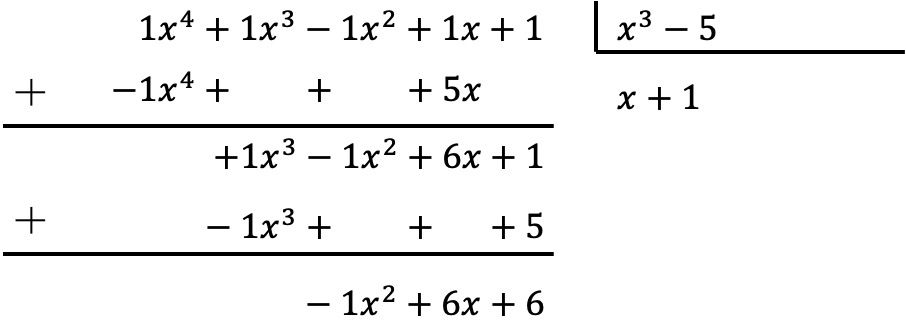
Dolayısıyla iki polinom arasındaki bölümün sonucu:

Bölüm:

Dinlenmek:

Alıştırma 5

Aşağıdaki polinom bölümünü hesaplayın:

Polinomun binomla bölünmesini çözmek için yukarıda gördüğümüz yöntemi uygulamalıyız:

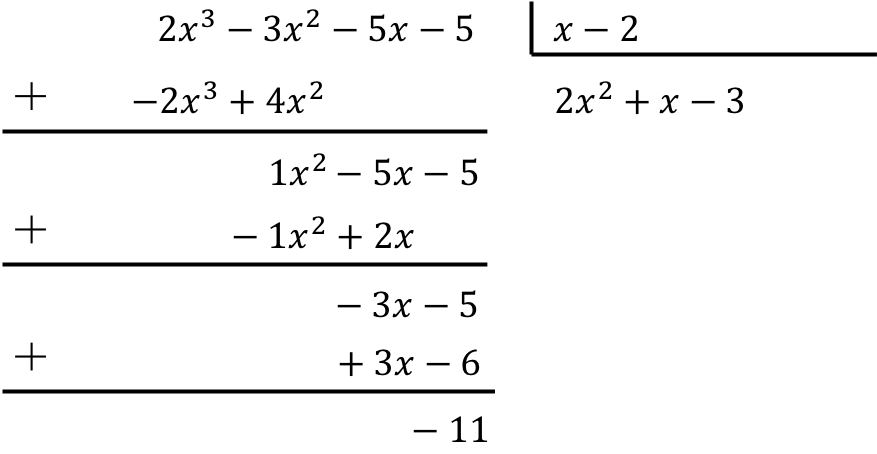
Dolayısıyla polinom bölümünün sonucu şu şekildedir:

Bölüm:

Dinlenmek:

Alıştırma 6

Aşağıdaki polinom bölümünü çözün:

Polinomların bölünmesini hesaplamak için açıklanan yöntemi uygulamamız gerekir:

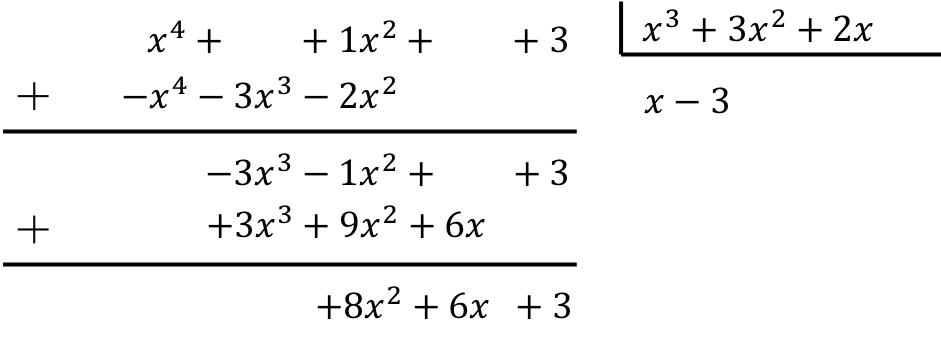
Dolayısıyla iki polinom arasındaki bölümün sonucu:

Bölüm:

Dinlenmek:

Egzersiz 7

2 polinom arasında aşağıdaki bölme işleminin sonucunu bulun:

Polinomun trinomiye bölünmesini hesaplamak için açıklanan yöntemi uygulamanız gerekir:

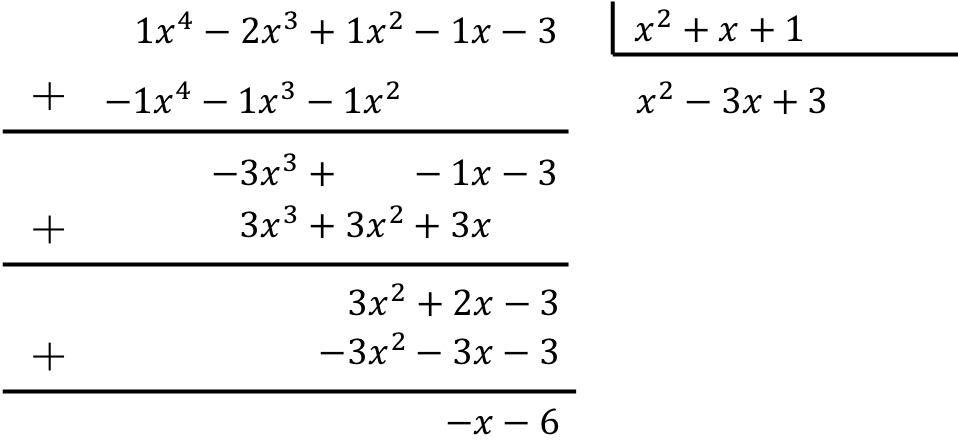
Dolayısıyla iki polinom arasındaki bölümün sonucu:

Bölüm:

Dinlenmek:

👉👉👉Buraya kadar geldiyseniz polinomların nasıl bölündüğünü zaten biliyorsunuz demektir. Parlak! Artık polinomların bölünmesi konusunda uzmanlaştığınıza göre, polinomlar arasındaki belirli bölmeleri çok daha hızlı çözmenize olanak tanıyan bir yöntem olduğunu bilin. Bu sentetik bir bölme veya Ruffini kuralıdır , bu hilenin nasıl uygulandığını ve ne zaman kullanılabileceğini linke tıklayarak görebilirsiniz.😉