Tek terimli işlemler

Bu sayfada tek terimli işlemlerle (toplama, çıkarma, çarpma, bölme ve kuvvet) tüm işlemlerin nasıl yapılacağını açıklıyoruz. Ayrıca tek terimli işlemlerle her türlü işlemin örneklerini görebileceksiniz ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Tek terimlilerin eklenmesi ve çıkarılması

İki veya daha fazla tek terimli yalnızca benzer tek terimliyse, yani iki tek terimlinin aynı değişmez kısmı varsa (aynı harfler ve aynı üsler) toplanabilir veya çıkarılabilir.

Daha sonra, iki benzer monomiyalin toplamı (veya çıkarılması), aynı değişmez kısımdan oluşan başka bir monom ve bu iki monomiyalın katsayılarının toplamına (veya çıkarılmasına) eşittir.

Tek terimlilerin toplanması ve çıkarılması aynı zamanda sırasıyla tek terimlilerin toplanması ve çıkarılması olarak da adlandırılır.

Tek terimlilerin toplanması ve çıkarılması örnekleri

İki veya daha fazla tek terimli sayının nasıl toplanıp çıkarılacağını net bir şekilde anlayabilmeniz için aşağıda birkaç örnek bırakıyoruz:

• 

• 

• 

• 

• 

Son örnekteki monomlar benzer olmadıklarından veya başka bir deyişle farklı bilinmeyenlere veya üslere sahip olduklarından eklenemez veya çıkarılamaz.

Bir tek terimlinin birkaç katının çarpımı

Bir tek terimlinin çarpımını bir sayıyla çözmek için, tek terimlinin gerçek kısmını aynı bırakarak, tek terimlinin katsayısını bu sayıyla çarpmanız yeterlidir.

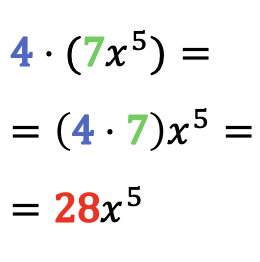
Sayıları tek terimlilerle çarpma örnekleri

• 

• 

• 

• 

Tek terimlilerin çarpımı

İki monomlunun çarpımının sonucu, katsayısı monomluların katsayılarının çarpımı olan ve gerçek kısmı aynı tabana sahip değişkenlerin çarpılmasıyla yani üslerinin toplanmasıyla elde edilen başka bir monomdur.

Bu nedenle iki farklı tek terimliyi çarpmak için aralarındaki katsayıları çarpmamız ve aynı tabana sahip kuvvetlerin üslerini toplamamız gerekir.

Ancak taban kuvvetleri farklı iki tek terimliyi çarparsak , katsayılarını birlikte çarpmamız ve kuvvetlerini aynı bırakmamız yeterlidir. Örneğin:

Öte yandan, tek terimlileri çarparken işaret kuralı dikkate alınmalıdır:

• Pozitif bir tek terimlinin pozitif bir tek terimle çarpılması başka bir pozitif tek terimliyi verir.
• Pozitif bir tek terimlinin negatif bir tek terimle çarpılması (veya tam tersi), negatif bir tek terimliye eşittir.
• İki negatif tek terimlinin çarpımı pozitif bir tek terimliyi oluşturur.

Tek terimli çarpma örnekleri

Aşağıda tek terimli sayılar arasında çarpma işleminin birkaç örneği verilmiştir, böylece nasıl yapıldığını görebilirsiniz:

• 

• 

• 

• 

• 

Gördüğünüz gibi tek terimlilerin çarpımını çözmek nispeten basittir. Ancak tek terimlilerin polinomlarla da çarpılabileceğini, hatta 2 veya daha fazla polinomun birlikte çarpılabileceğini de unutmamalısınız. Daha fazla ilgileniyorsanız polinom çarpımına tıklayarak tüm bu işlemlerin nasıl çalıştığını görebilirsiniz.

Tek terimlilerin bölünmesi

Matematikte, monomların bölünmesinin sonucu, katsayısı monomların katsayılarının bölümüne eşit olan ve gerçek kısmı aynı tabana sahip değişkenlere bölünerek, yani üslerinin çıkarılmasıyla elde edilen başka bir monomdur. .

Açıkçası, tek terimlilerin herhangi bir bölümü kesir olarak da ifade edilebilir:

Çarpmada olduğu gibi, tek terimlilerin bölünmesinde de işaretler yasasını uygulamak gerekir:

• Pozitif bir tek terimlinin pozitif bir tek terime bölünmesi başka bir pozitif tek terimliyi verir.
• Pozitif bir tek terimlinin negatif bir tek terimliye bölünmesi (veya tam tersi), negatif bir tek terimliye eşdeğerdir.
• Birbirine bölünen iki negatif tek terimli, pozitif bir tek terimliyi doğurur.

Tek terimlilerin bölünmesine örnekler

Aşağıda iki veya daha fazla tek terimlinin nasıl bölündüğüne dair daha fazla örnek görebilirsiniz:

• 

• 

• 

• 

• 

Elbette bir noktada matematikte yeni bir şey öğrendiğinizde kendinize şu soruyu sormuşsunuzdur: Bu ne için ? Polinomları bölmek için tek terimli bölme kullanılır. Aslında, iki tek terimlinin yanlış bölünmesi nedeniyle polinomları bölerken hata yapmak oldukça yaygındır. Bu nedenle, artık tek terimlilerin bölünmesine aşina olduğunuza göre, polinomların bölünmesinin nasıl hesaplandığını görmenizi öneririz, çünkü artık prosedürü öğrenmek sizin için çok daha kolay olacaktır (oldukça karmaşıktır).

Bir monomialin gücü

Matematikte, bir tek terimlinin kuvvetini hesaplamak için, tek terimlinin her bir öğesi kuvvetin üssüne yükseltilir . Başka bir deyişle, bir monomiyalin kuvveti, katsayısını ve değişkenlerini (harflerini) kuvvetin üssüne yükseltmekten ibarettir.

Üslerin özelliklerinden, her ikisi de zaten yüksek olan bir terimi yükseltirken üslerin çoğaldığını unutmayın. Bu nedenle , bir tek terimlinin kuvvetine göre, her harfin üssü daima kuvveti gösteren üs ile çarpılır .

Öte yandan, bu işlemi doğru bir şekilde gerçekleştirmek için yetkilerin aşağıdaki özelliğini hatırlamanız gerekir:

• Çift bir üs değerine yükseltilen negatif bir tek terim, pozitif bir tek terime eşdeğerdir.
• Bunun yerine, tek terimli bir üsse yükseltilen negatif bir tek terim, negatif bir tek terimle sonuçlanır.

Tek terimlilerin kuvvetlerine örnekler

Monomiyalin kuvvetinin nasıl hesaplandığını net bir şekilde anlayabilmeniz için size bazı örnekler bırakıyoruz:

• 

• 

• 

• 

• 

Tek terimlilerle birleştirilmiş işlemler

Tek terimlilerle yapılan tüm işlemlerin ne olduğunu gördükten sonra bunların birbirleriyle de birleştirilebileceğini bilin. Yani, toplama, çıkarma, çarpma, bölme ve kuvvetler gibi tüm türlerin dahil olduğu tek terimli işlemleri çözmemizin istendiği alıştırmalar bulabiliriz.

Ama endişelenmeyin, göründükleri kadar zor değiller. Hatırlamanız gereken tek şey, birleştirilmiş işlemlerin çözümlenme sırasıdır:

1. Öncelikle parantez içindeki tek terimli işlemler çözülür.
2. Daha sonra monomların kuvvetleri hesaplanır.
3. Üçüncüsü, tek terimlilerin çarpımları ve bölmeleri gerçekleştirilir.
4. Son olarak tek terimlilerin toplama ve çıkarma işlemleri belirlenir.

Bir örneği çözerek daha net göreceğinize eminim:

Tek terimlilerin birleşik işlemine örnek

Öncelikle parantez içindeki tek terimli işlemleri çözmeliyiz:

Bu durumda gücümüz yok. Şimdi tek terimlilerin çarpımlarını ve bölümlerini hesaplayalım:

Ve son olarak tek terimlileri ekleyip çıkarıyoruz:

Tek terimli işlemlerle ilgili çözülmüş alıştırmalar

Pratik yapmak isterseniz, tek terimli işlemlerde ESO zorluk derecesini adım adım çözebileceğiniz birkaç alıştırmayı aşağıda bırakıyoruz.

1. Egzersiz

Aşağıdaki tek terimlilerin toplama ve çıkarma işlemlerini hesaplayın:

Alıştırma 2

Aşağıdaki monomların çarpımlarını çözün: