▷ Bir fonksiyonun içbükeyliği ve dışbükeyliği (eğrilik)

Burada bir fonksiyonun içbükey ve dışbükeyliğinin ne olduğunu ve bir fonksiyonun içbükey mi yoksa dışbükey mi olduğunu nasıl anlayacağınızı öğreneceksiniz. Ayrıca bir fonksiyonun eğriliği üzerine adım adım alıştırmalar yapabileceksiniz.

Bir fonksiyonun içbükeyliği ve dışbükeyliği nedir?

Bir fonksiyonun içbükeyliği ve dışbükeyliği, bir fonksiyonun grafiğinin eğriliğini ifade eder. İçbükey fonksiyon , grafiği dağ şeklinde olan bir fonksiyondur ve dışbükey fonksiyon , grafiği vadi şeklinde olan bir fonksiyondur.

Önceki paragrafta, içbükey ve dışbükey fonksiyonlar, anlaşılmasını kolaylaştırmak için gayri resmi olarak tanımlanmıştı, ancak içbükey fonksiyon ve dışbükey fonksiyonun matematiksel tanımı aşağıdaki gibidir:

İçbükey fonksiyon: Fonksiyonun herhangi iki noktasını birleştiren doğru parçası eğrinin altında olduğunda.
Dışbükey fonksiyon: Fonksiyonun herhangi iki noktasını birleştiren doğru parçası eğrinin üzerinde olduğunda.

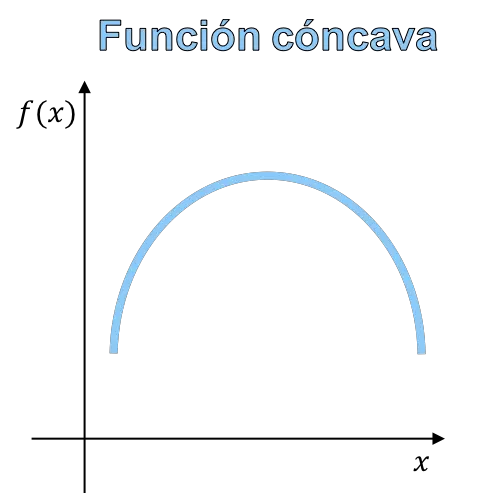
Sonuçta, içbükey fonksiyon ile dışbükey fonksiyon arasındaki fark fonksiyonun şeklindedir ve dolayısıyla fonksiyonun grafiğinden içbükeyliği dışbükeylikten ayırt edebilirsiniz.

Bununla birlikte, bir fonksiyonun tüm tanım kümesi boyunca mutlaka içbükey veya dışbükey olması gerekmez; aynı zamanda bir aralıkta içbükey ve başka bir aralıkta dışbükey olabilir.

Not: Matematik camiası hala tam olarak aynı fikirde değil ve bu nedenle bazı profesörler bunun tersini söylüyor: bir fonksiyona içbükey bir fonksiyon diyorlar.

$\bm{\cup}$

ve formuna sahip bir dışbükey fonksiyon

$\bm{\cap}$

. Her durumda önemli olan, adı ne olursa olsun işlevin ne olduğunu bilmektir.

Bir fonksiyonun eğriliği nasıl incelenir

Bir fonksiyonun eğriliğini incelemek, fonksiyonun içbükeyliğini ve dışbükeyliğini bulmayı, yani fonksiyonun içbükey olduğu aralıkları ve dışbükey olduğu aralıkları bilmeyi içerir.

Dolayısıyla bir fonksiyonun eğriliğini incelemek için aşağıdaki adımlar gerçekleştirilmelidir:

Fonksiyonun tanım kümesine ait olmayan noktaları bulun.
Fonksiyonun birinci türevini ve ikinci türevini hesaplayın.
İkinci türevin köklerini bulun, yani ikinci türevi iptal eden noktaları çözerek hesaplayın
$f''(x)=0$

.
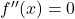
Türevin kökleri ve fonksiyonun tanım kümesine ait olmayan noktalar ile aralıklar oluşturun.
Her aralığın bir noktasında ikinci türevin değerini hesaplayın.
Böylece, ikinci türevin işareti, fonksiyonun bu aralıktaki içbükeyliğini veya dışbükeyliğini belirler:
- Fonksiyonun ikinci türevi pozitifse fonksiyon bu aralıkta dışbükeydir .
- Fonksiyonun ikinci türevi negatif ise fonksiyon bu aralıkta içbükeydir .

Bir fonksiyonun eğriliğinin nasıl bulunacağına dair örnek

Daha sonra, bir fonksiyonun içbükeylik ve dışbükeylik aralıklarının nasıl hesaplandığını görebilmeniz için bir örneği adım adım çözeceğiz.

Aşağıdaki fonksiyonun içbükeyliğini ve dışbükeyliğini inceleyin:

$f(x)=x^3-3x$

Yapılacak ilk şey fonksiyonun tanım tanım kümesini hesaplamaktır. Bu durumda bir polinom fonksiyonumuz var, yani fonksiyonun tanım kümesi gerçek sayılardan oluşuyor:

$\text{Dom } f= \mathbb{R}$

Fonksiyonun tanım kümesini hesapladıktan sonra fonksiyonun ikinci türevinin hangi noktalarda sıfır olduğunu araştırmamız gerekir.

Bu nedenle fonksiyonun birinci türevini hesaplıyoruz:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

Daha sonra fonksiyonun ikinci türevini buluruz:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Fonksiyonun tanım kümesini hesapladıktan sonra

$f''(x)=0$

, çizgi üzerinde bulunan tüm kritik noktaları temsil ediyoruz. Bu durumda fonksiyonun tanım kümesinin hesaplanmasında herhangi bir kritik nokta bulamadık ancak fonksiyonun ikinci türevini iptal eden bir nokta elde ettik:

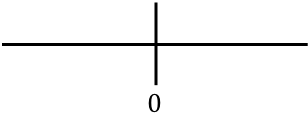
Şimdi fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktaları değil) ve bu noktada ikinci türevin hangi işarete sahip olduğuna bakıyoruz:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Son olarak fonksiyonun içbükeylik ve dışbükeylik aralıklarını çıkarıyoruz. İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Böylece fonksiyonun içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(0,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,0)}$

Bir fonksiyonun içbükeyliği ve dışbükeyliği ile ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki polinom fonksiyonunun içbükeylik ve dışbükeylik aralıklarını hesaplayın:

$f(x) = x^3-3x^2-2x$

Çözümü görün

Alıştırmadaki fonksiyon bir polinom olduğundan fonksiyonun tanım kümesi gerçek sayılardan oluşur:

$\text{Dom } f= \mathbb{R}$

Fonksiyonun tanım kümesini belirledikten sonra onu farklılaştırıyoruz:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

Daha sonra fonksiyonun ikinci türevini buluruz:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Fonksiyonun tanım kümesini hesaplayıp çözdükten sonra

$f''(x)=0$

sayı doğrusunda bulunan tüm tekil noktaları temsil ediyoruz:

Şimdi her aralığa ait bir nokta alalım ve bu noktada ikinci türevinin hangi işarete sahip olduğunu görelim:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

İkinci türevin sıfırdan büyük olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

, ancak ikinci türev negatif olduğunda bu, fonksiyonun içbükey olduğu anlamına gelir.

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(1,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Alıştırma 2

Aşağıdaki rasyonel fonksiyonun eğriliğini inceleyin:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Çözümü görün

Öncelikle fonksiyonun tanım kümesini hesaplamamız gerekiyor. Bu rasyonel bir fonksiyon olduğundan, hangi sayıların fonksiyonun tanım kümesine ait olmadığını görmek için paydayı sıfıra eşitliyoruz:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Bu, x -2 veya +2 olduğunda paydanın 0 olacağı anlamına gelir. Dolayısıyla fonksiyon mevcut olmayacaktır. Dolayısıyla fonksiyonun tanım kümesi x=-2 ve x=+2 dışındaki tüm sayılardan oluşur.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

İkinci olarak fonksiyonun birinci türevini hesaplıyoruz:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Daha sonra ikinci türevi çözüyoruz:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tüm terimler çarpılır

$(x^2-4)$

. Bu nedenle kesri basitleştirebiliriz:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Şimdi fonksiyonun ikinci türevinin köklerini hesaplayalım:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Dönem

$\left(x^2-4\right)^3$

Bu, sol tarafın tamamını bölmeyi içerir, böylece bunu sağ tarafın tamamıyla çarpabiliriz:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Ortak çarpanı çıkarıyoruz:

$x(8x^2+96)=0$

Çarpmanın 0’a eşit olması için çarpımın iki unsurundan birinin sıfır olması gerekir. Bu nedenle her faktörü 0’a eşitliyoruz:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Reel sayının negatif kökü olmadığı için çözüm de yoktur.

Şimdi elde edilen tüm kritik noktaları, yani tanım kümesine ait olmayan noktaları (x=-2 ve x=+2) ve ikinci türevi (x=0) iptal eden noktaları doğru üzerinde temsil ediyoruz:

Ve fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendiririz. Yani her aralıkta bir nokta alıyoruz ve o noktada hangi işaretin ikinci türevine sahip olduğuna bakıyoruz:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Alıştırma 3

Bir işlev

$f(x)$

nispeten aşırı bir durum var

$x=3$

. Dahası, fonksiyon dışbükeydir

$(\cup )$

aynı noktada. Göreceli uç noktanın minimum mu yoksa maksimum mu olduğunu belirleyin.

➤ Bakınız: bir fonksiyonun maksimum ve minimumlarının tanımı

Çözümü görün

Dışbükey fonksiyona izin verin

$(\cup)$

İçinde

$x=3$

bu noktadaki ikinci türevin pozitif olduğu anlamına gelir, yani

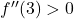$f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class=$ Bu nedenle göreceli ekstremum

$\bm{x=3}$

Bu minimumdur , çünkü

$f''(3)$

Olumlu.

Bir fonksiyonun içbükeyliği ve dışbükeyliği nedir?

Bir fonksiyonun eğriliği nasıl incelenir

Bir fonksiyonun eğriliğinin nasıl bulunacağına dair örnek

Bir fonksiyonun içbükeyliği ve dışbükeyliği ile ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Yorum bırakın Yanıtı iptal et