Burada fonksiyon optimizasyon problemlerinin aşamalı olarak nasıl çözüldüğünü açıklıyoruz. Ayrıca optimizasyon problemleri üzerine çözülmüş alıştırmalar ile pratik yapabileceksiniz.
Optimizasyon sorunları nelerdir?
Optimizasyon problemleri, bir fonksiyonun maksimum veya minimumunu bulmanın gerekli olduğu problemlerdir. Örneğin bir optimizasyon problemi, bir şirketin karını tanımlayan bir fonksiyonun maksimumunun hesaplanmasını içerir.
Optimizasyon sorunları nasıl çözülür?
İşlev optimizasyonu sorunlarını çözme adımları:
- Optimize edilmesi gereken işlevi ayarlayın .
- Optimize edilecek fonksiyonu türetin.
- Optimize edilecek fonksiyonun kritik noktalarını bulun. Bunu yapmak için fonksiyonun türevini sıfıra eşitlemeniz ve ortaya çıkan denklemi çözmeniz gerekir.
- Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Bir optimizasyon problemine örnek
Optimizasyon problemleri teorisini göz önünde bulundurarak, bu tür bir problemi adım adım çözeceğiz, böylece nasıl gerçekleştirildiklerini görebilirsiniz.
- Bacaklarının toplamı 10 cm olan dik üçgenlerden maksimum yüzey alanına sahip olanın boyutlarını hesaplayınız.
Sorunu çözmek için üçgenin bir dalını x , diğer dalını ise y olarak adlandıracağız:

Adım 1: Optimize edilecek işlevi ayarlayın.
Üçgenin alanının maksimum olmasını istiyoruz ve üçgenin alan formülü şu şekildedir:
![]()
Bizim durumumuzda üçgenin tabanı x ve yüksekliği y’dir . Henüz:
![]()
Optimize edecek fonksiyonumuz zaten var, ancak bu iki değişkene bağlıyken yalnızca bir değişkene bağlı olabilir. Ancak açıklamada iki bacağın toplamının 10 cm olması gerektiği belirtiliyor. Henüz:
![]()
Bu denklemden y’yi çözüyoruz:
![]()
Ve ifadeyi fonksiyonun yerine koyarız:
![]()
![]()
Artık planlı optimizasyon fonksiyonumuz var ve bu sadece bir değişkene bağlı, dolayısıyla bir sonraki adıma geçebiliriz.
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
Bu rasyonel bir fonksiyondur, dolayısıyla bunu türetmek için bölmenin türevinin formülünü uygularız:
![]()
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için türevi sıfıra eşitlememiz ve sonuç denklemini çözmemiz gerekir:
![]()
![]()
4, sol tarafın tamamını böldüğü için sağ tarafın tamamını çarparak bunu çarpabiliriz:
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu incelemek için sağda bulunan kritik noktayı temsil ediyoruz:
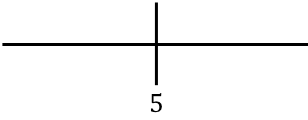
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bunu yapmak için her aralıkta bir nokta alırız (asla kritik noktayı değil) ve türevin o noktada hangi işarete sahip olduğuna bakarız:
![]()
![]()
![]()
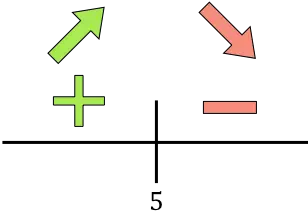
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Bu nedenle, fonksiyonu artırma ve azaltma aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
x=5’te fonksiyon artandan azalan tarafa doğru gider, dolayısıyla x=5 optimize edilecek fonksiyonun göreceli maksimumudur .
Dolayısıyla x=5 üçgenin maksimum alana sahip dalının değeridir. Basitçe diğer bacağın değerini hesaplayın:
![]()
Sonuç olarak üçgenin maksimum alanını maksimuma çıkaran değerler şunlardır:
![]()
![]()
Optimizasyon sorunları çözüldü
Sorun 1
İlaç hasta kişiye verilir ve
![]()
Birkaç saat sonra aktif bileşenin kan konsantrasyonu fonksiyon tarafından verilir.
![]()
mililitre başına miligram. Maksimum değerini belirleyin
![]()
ve söz konusu değere ne zaman ulaşıldığını gösterir.
Adım 1: Optimize edilecek işlevi ayarlayın.
Bu problemde bize zaten önerilen fonksiyonu veriyorlar ki bu da
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
Fonksiyon 2 fonksiyonun çarpımından oluşur. Bu nedenle, fonksiyonun türevini hesaplamak için çarpımın türevine ilişkin kuralı uygulamamız gerekir:
![]()
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
Denklemi çözmek için ortak faktörü alıyoruz:
![]()
Çarpmanın 0’a eşit olması için çarpımın iki unsurundan birinin sıfır olması gerekir. Bu nedenle her faktörü 0’a eşitliyoruz:
![Rendered by QuickLaTeX.com \displaystyle e^{-t/2}\cdot \left(1 - \frac{1}{2}t \right) = 0 \longrightarrow \begin{cases} e^{-t/2}=0 \ \bm{\times} \\[2ex]\displaystyle 1 - \frac{1}{2}t=0 \ \longrightarrow \ 1= \frac{1}{2}t \ \longrightarrow \ \bm{2=t} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8390139724dbc4ad014db2a76e508290_l3.png)
Başka bir sayıya yükseltilmiş bir sayı asla 0 veremez, bu nedenle,
![]()
Çözümü yok.
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu incelemek için sağda bulunan kritik noktayı temsil ediyoruz:
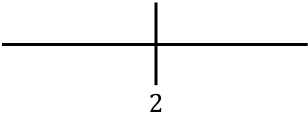
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
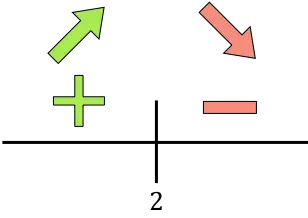
Türev pozitifse fonksiyon artıyor demektir, türev negatifse fonksiyon azalıyor demektir. Böylece optimize edilecek fonksiyonun büyüme ve azalma aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon t=2’de artandan azalan tarafa doğru gider, yani t=2 fonksiyonun maksimumudur . Bu nedenle maksimum konsantrasyona t=2 saatte ulaşılacaktır.
Son olarak, maksimum konsantrasyonun değerini bulmak için maksimumun oluştuğu değeri orijinal fonksiyonla değiştiririz:
![]()
Sorun 2
Bir mağaza, scooter başına 1.000 € fiyatla 40 elektrikli scooter satmayı umuyor. Ancak pazar araştırmasına göre, scooter fiyatındaki her 50 €’luk düşüş, en çok satan 10 scooter’ın satışlarında bir artış olacak.
İlk olarak, scooter’ın orijinal 1000 $’lık fiyatının kaç kez 50 $ düştüğünü temel alarak mağazanın gelir fonksiyonunu yazın. Daha sonra maksimum kar elde etmek için scooterın fiyatını ve bu fiyattan elde edilen geliri belirleyin.
Adım 1: Optimize edilecek işlevi ayarlayın.
Sorun ifadesi bize bir ipucu veriyor çünkü fonksiyonun başlangıç fiyatındaki 50$’lık azalma sayısına bağlı olması gerektiğini söylüyor. Bu nedenle fiyatın 50€ kadar azaldığı sayıya x diyeceğiz:
![]()
€
Gelir fonksiyonu, satılan scooter sayısı ile her bir scooterın fiyatının çarpımı olacaktır:
![]()
Satılan scooter sayısı, her 50 €’luk fiyat indirimi için 40 artı 10 scooter olacaktır. Henüz:
![]()
Her bir scooterın fiyatı başlangıçta 1000 € olacak ve her fiyat düşüşünde 50 € azalacak. Henüz:
![]()
Bu nedenle sorunu optimize edecek fonksiyon şudur:
![]()
![]()
![]()
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
Polinom bir fonksiyon olduğundan türevi hesaplamak daha kolaydır:
![]()
Adım 3: Fonksiyonun kritik noktalarını bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu incelemek için sayı doğrusunda hesaplanan kritik noktayı temsil ederiz:
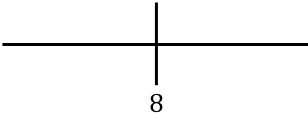
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
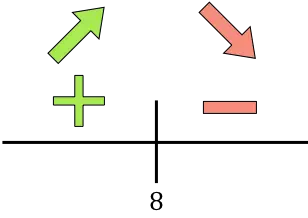
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon x=8’de artandan azalana doğru gider, dolayısıyla x=8 fonksiyonun maksimumudur . Bu nedenle maksimum gelir 50€’luk indirimin 8 katı yapılarak elde edilecektir.
Şimdi maksimum gelirin değerini bulmak için maksimum gelirin göründüğü değeri orijinal fonksiyona yerleştireceğiz:
![]()
![]()
€
Ve 8 kez 50€’luk indirim yapıldıktan sonra her scooter’ın fiyatı şu şekilde olacaktır:
![]()
![]()
€
Sorun 3
Bir şirketin maliyet fonksiyonu (bin euro cinsinden) aşağıdaki ifade kullanılarak belirlenebilir:
![]()
Altın
![]()
Belirli bir öğeden üretilen binlerce birimi temsil eder.
Maliyetin minimum olması için ne kadar üretilmesi gerektiğini, bu maliyetin ne olduğunu ve bu kalemlerden hiçbiri üretilmeseydi maliyetin ne olacağını belirleyin.
Adım 1: Optimize edilecek işlevi ayarlayın.
Sorun bildirimi zaten bize optimize edilecek fonksiyonu sağlıyor;
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Sağda bulunan kritik noktayı temsil ediyoruz:
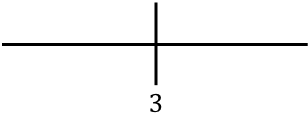
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
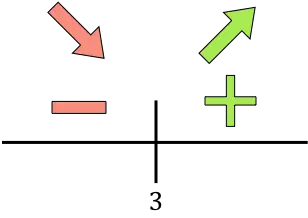
Türev sıfırdan büyükse fonksiyon bu aralıkta artar. Öte yandan türev sıfırdan küçükse fonksiyon bu aralıkta azalır. Buna göre fonksiyonun artış ve azalış aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon x=3’te azalıştan artmaya doğru gider, dolayısıyla x=3 fonksiyonun minimumudur . Dolayısıyla 3.000 adet üretilerek minimum maliyete ulaşılacak.
Şimdi minimum maliyet değerini bulmak için minimum maliyete ulaşılan değeri orijinal fonksiyona yerleştireceğiz:
![]()
milyonlarca avro.
Bir yandan da hiçbir şey üretilmeseydi, yani ne zaman üretilseydi maliyeti ne olurdu diye soruyorlar bize.
![]()
Bu nedenle hesaplamak gerekir
![]()
![]()
milyonlarca avro.
Sorun 4
2 m2’lik alanı sınırlayan dikdörtgen bir ahşap çerçeve inşa etmek istiyoruz. Ahşabın fiyatının yatay kenarlarda 7,5€/m, dikey kenarlarda ise 12,5€/m olduğunu biliyoruz. Çerçevenin toplam maliyetinin mümkün olan en düşük ve söz konusu maliyetin en düşük olması için dikdörtgenin sahip olması gereken boyutları belirleyin.
Adım 1: Optimize edilecek işlevi ayarlayın.
Sorunu çözmek için yatay tarafa x ve dikey tarafa y adını vereceğiz:

Yatay tarafı satın almanın maliyeti 7,5 €, dikey tarafı satın almanın maliyeti ise 12,5 €’dur. Ek olarak, her çerçeve için iki yatay kenara ve iki dikey kenara ihtiyacımız var. Bu nedenle çerçevenin maliyeti aşağıdaki fonksiyonla belirlenebilir:
![]()
Optimize etme fonksiyonumuz zaten var. Ancak yalnızca bir değişkene bağlı olabileceği zaman iki değişkene bağlıdır. Ancak açıklama bize çerçevenin yüzey alanının 2 m2 olması gerektiğini söylüyor. Henüz:
![]()
y değişkenini siliyoruz:
![]()
Optimize edilecek fonksiyonda bulunan ifadeyi yerine koyarız:
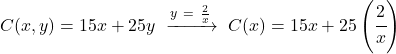
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
![]()
![]()
![]()
Denklemi kesirlerle çözmek için enine çarpıyoruz:
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu analiz etmek için bulunan kritik noktayı çizgi üzerinde temsil ediyoruz:
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon x=1,83’te azalmadan artmaya değişir, dolayısıyla x=1,83 fonksiyonun minimumudur .
Dolayısıyla x=1,83 minimum maliyeti temsil eden yatay tarafın değeridir. Şimdi dikey tarafın değerini hesaplayalım:
![]()
Böylece minimum çerçeve maliyetini oluşturan değerler şunlardır:
yatay taraf
![]()
dikey taraf
![]()
Ve bu değerlerle ulaşılan minimum maliyet:
![]()
€
Sorun 5
Bir katedralin kapısı, aşağıdaki şekilde gösterildiği gibi, iki sütunla desteklenen yarım çembersel bir kemerden oluşmaktadır:
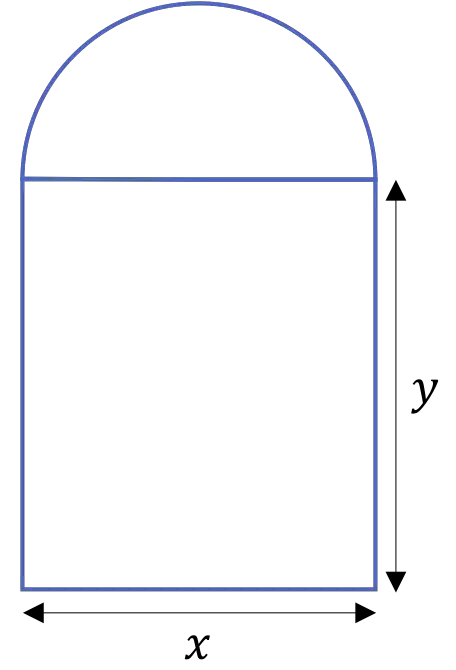
Kapının çevresi 20 m ise ölçülerini belirleyiniz.
![]()
Ve
![]()
bu da tüm kapının yüzey alanını maksimuma çıkarır.
Adım 1: Optimize edilecek işlevi ayarlayın.
Bir dairenin alanı formülle hesaplanır
![]()
Yani tüm kapının alanı dikdörtgenin alanı artı çevrenin alanının yarısı olacaktır:
![]()
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \left(\cfrac{x}{2}\right)^2 \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-baa2e14b061cf14a657782db8fe91b92_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y + \cfrac{1}{2} \left[ \pi \cdot \cfrac{x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9196d8284edebe6450d49aa5a0b6a3e1_l3.png)
![Rendered by QuickLaTeX.com A(x,y)= x y +\cfrac{1}{2} \left[ \cfrac{\pi \cdot x^2}{4} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-b25e1d2c661585be998d1596d6650c01_l3.png)
![]()
Optimize etme fonksiyonumuz zaten var. Ancak yalnızca bir değişkene bağlı olabileceği zaman iki değişkene bağlıdır.
Ancak açıklama bize tüm kapının çevresinin 20 metre olduğunu söylüyor. Bir dairenin çevresi formülle hesaplanır
![]()
Bu nedenle tüm kapının çevresi şöyle olacaktır:
![Rendered by QuickLaTeX.com P= x +2y +\cfrac{1}{2} \left[ 2 \pi \left( \cfrac{x}{2}\right) \right] = x+2y + \cfrac{2 \pi x }{2 \cdot 2} = x+2y + \cfrac{ \pi x }{2 }](https://mathority.org/wp-content/ql-cache/quicklatex.com-7709d0c72bf84a17ac83bc46f5cce002_l3.png)
Çevre 20 m olmalıdır. Bu nedenle, arasındaki ilişkiyi bulmak için önceki ifadeyi 20’ye eşitledik.
![]()
Ve
![]()
![]()
Kesirleri elemek için tüm terimleri 2 ile çarpıyoruz:
![]()
![]()
Temizliyoruz
![]()
![]()
![]()
Optimize edilecek fonksiyonda bulunan ifadeyi yerine koyarız:
![]()
![]()
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
![]()
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
Bu kesirli bir denklemdir, dolayısıyla kesirleri ortadan kaldırmak için her terimi paydaların lcm’si ile çarparız:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu incelemek için sağda bulunan kritik noktayı temsil ediyoruz:
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon x=5,6’da artandan azalana doğru gider, dolayısıyla x=5,6 fonksiyonun maksimumudur .
Henüz,
![]()
maksimum yüzeyi oluşturan değerdir. Şimdi değerini hesaplıyoruz
![]()
![]()
Böylece maksimum yüzeyi oluşturan değerler şunlardır:
![]()
![]()
Sorun 6
Alanı 54 cm2 olan silindir şeklinde bir tank yapmak istiyoruz. Hacmin maksimum olması için tabanın yarıçapını ve silindirin yüksekliğini belirleyin.
Adım 1: Optimize edilecek işlevi ayarlayın.
Silindirin hacmi aşağıdaki formülle hesaplanır:
![]()
Tabanın alanı bir daire olduğundan formülü şu şekildedir:
![]()
. Dolayısıyla silindirin hacminin formülü şu şekildedir:
![]()
Optimize etme fonksiyonumuz zaten var. Ancak bu iki değişkene bağlıdır (
![]()
Ve
![]()
) ancak yalnızca birine bağlı olabilir. Ancak ifade bize silindirin alanının 54 cm2 olması gerektiğini söylüyor, bu nedenle arasındaki ilişkiyi bulmak için bu koşuldan yararlanacağız.
![]()
Ve
![]()
Bir silindirin alanını hesaplamak için yan alanını iki tabanın alanlarıyla eklemelisiniz:
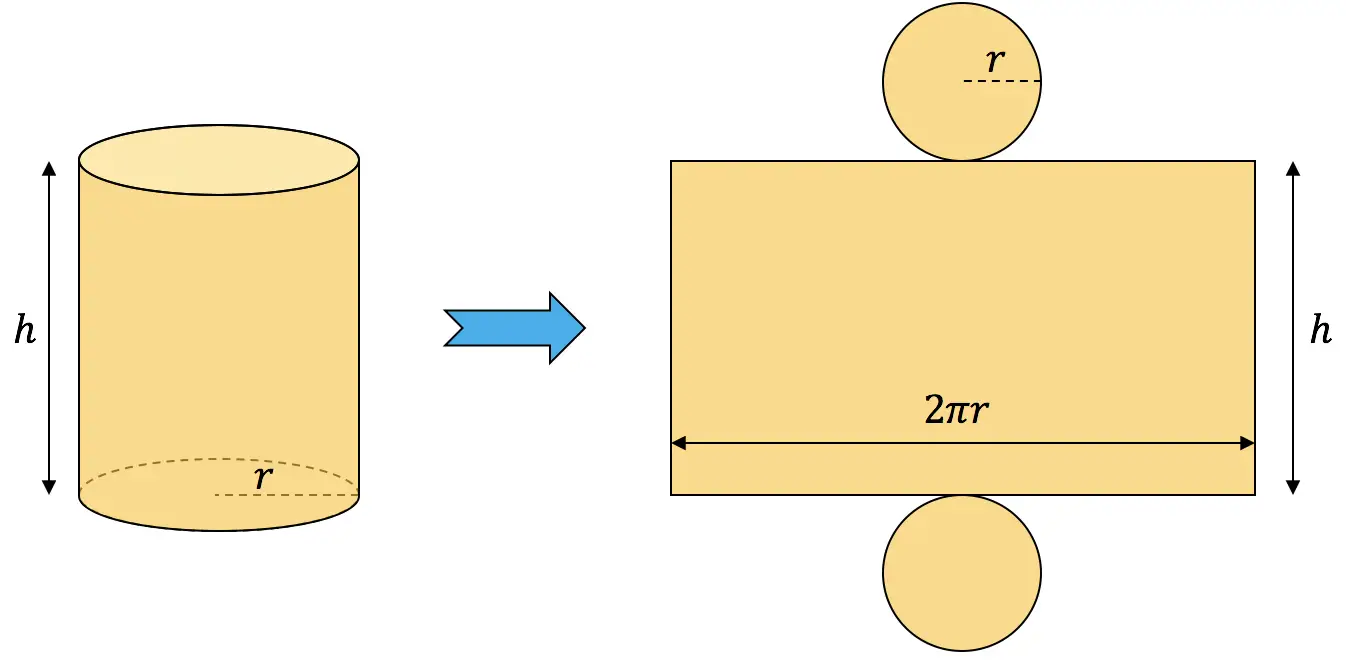
![]()
Silindirin alanı 54 cm2 olmalıdır, bu nedenle arasındaki ilişkiyi elde etmek için önceki ifadeyi 54’e eşitledik.
![]()
Ve
![]()
![]()
Temizliyoruz
![]()
![]()
![]()
Optimize edilecek fonksiyonda bulunan ifadeyi yerine koyarız:
![]()
![]()
![]()
Adım 2: Optimize edilecek fonksiyonun türevini hesaplayın.
![]()
Adım 3: Kritik noktaları bulun.
Fonksiyonun kritik noktalarını bulmak için çözüyoruz
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Adım 4: Fonksiyonun monotonluğunu inceleyin ve fonksiyonun maksimum veya minimumunu belirleyin.
Fonksiyonun monotonluğunu incelemek için sayı doğrusunda bulunan kritik noktayı temsil ediyoruz:
Şimdi fonksiyonun artan mı yoksa azalan mı olduğunu bulmak için her aralıkta türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktayı değil) ve bu noktada türevin hangi işarete sahip olduğuna bakıyoruz:
![]()
![]()
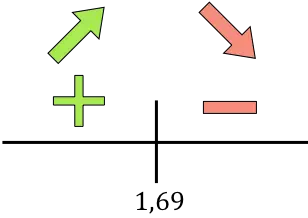
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:
Büyüme:
![]()
Azaltmak:
![]()
Fonksiyon r=1,69’da artandan azalan tarafa doğru gider, yani r=1,69 cm fonksiyonun maksimumudur .
Dolayısıyla r=1.69 maksimum hacmi oluşturan yarıçapın değeridir. Şimdi yüksekliği hesaplıyoruz:
![]()
Yani maksimum ses seviyesini oluşturan değerler şunlardır:
Radyo
![]()
Yükseklik
![]()