▷ Sekantın türevi (formül ve çözümlü alıştırmalar)

Burada bir fonksiyonun sekantının nasıl türetileceğini keşfedeceksiniz. Ayrıca sekantın türeviyle ilgili adım adım çözülmüş birkaç alıştırma görebileceksiniz. Ve son olarak bu tip trigonometrik türevin formülünün gösterimini bulacaksınız.

Sekantın türevi nedir?

X’in sekantının türevi, x’in sekantının ve x’in tanjantının çarpımına eşittir.

$f(x)=\text{sec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x)\cdot \text{tan}(x)$

Trigonometrik formüller uygulanarak, x’in sekantının türevi aynı zamanda sinüs x’in kosinüs x’in karesine bölümü olarak da tanımlanabilir.

$f'(x)=\text{sec}(x)\cdot \text{tan}(x)=\cfrac{1}{\text{cos}(x)}\cdot \cfrac{\text{sen}(x)}{\text{cos}(x)}=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

Ve eğer zincir kuralını uygularsak, bir fonksiyonun sekantının türevi, fonksiyonun sekantının çarpı fonksiyonun tanjantı çarpı fonksiyonun türevinin çarpımıdır.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

Özetle sekant fonksiyonunun türevinin formülü aşağıdaki gibidir:

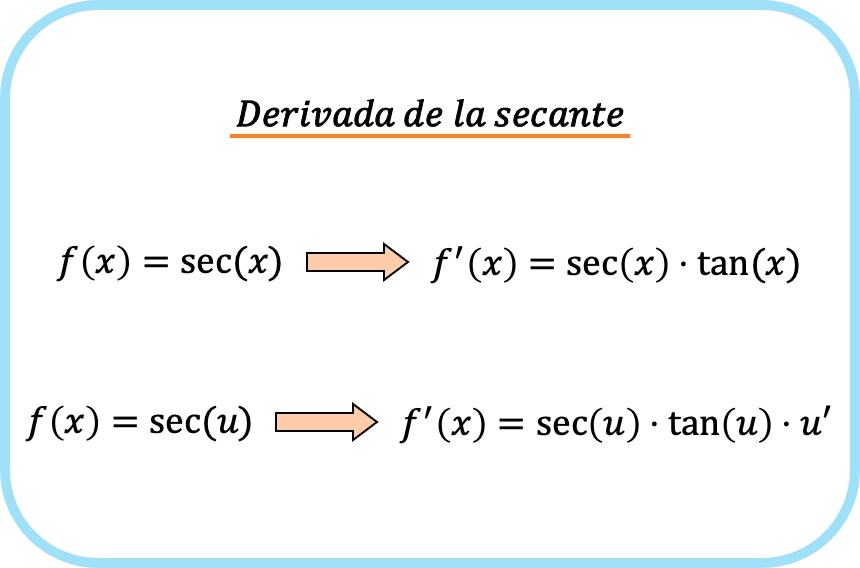
Sekantın türevine örnekler

Sekantın türevinin formülünün ne olduğunu gördükten sonra, bu tür trigonometrik türevlerin birkaç örneğini çözeceğiz.

Örnek 1: 2x’in sekantının türevi

Bu örnekte 2x’in sekantının türevinin ne kadar değerli olduğunu göreceğiz:

$f(x)=\text{sec}(2x)$

2x fonksiyonunun sekantını türetmek için ilgili formülü kullanmanız gerekir. Ayrıca sekant argümanında x dışında bir fonksiyonumuz var, dolayısıyla zincir kuralını uygulamamız gerekiyor.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

2x fonksiyonu doğrusal olduğundan türevi 2’dir. Bu nedenle, türevi bulmak için formülde u’yu 2x ve u”yu 2 ile değiştiririz:

$f(x)=\text{sec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(2x)\cdot \text{tan}(2x)\cdot 2$

Örnek 2: x karenin sekantının türevi

Bu alıştırmada x karenin sekantının türevinin ne olduğunu göreceğiz:

$f(x)=\text{sec}(x^2)$

Bir fonksiyonun sekantını türetmek için yukarıda görülen iki formülden birini kullanabilirsiniz, ancak bu durumda fonksiyonu sekant ve tanjant arasındaki çarpma formülüyle ayırt edeceğiz.

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

x’in 2’ye yükseltilmiş türevi 2x’i verir, dolayısıyla x karenin sekantının türevi şöyle olur:

$f(x)=\text{sec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(x^2)\cdot \text{tan}(x^2)\cdot 2x$

Örnek 3: Bir polinomun sekant küpünün türevi

$f(x)=\text{sec}^3(x^5+4x^2-3)$

Bir fonksiyonun sekantının türevine ilişkin kural şöyledir:

$f(x)=\text{sec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{sec}(u)\cdot \text{tan}(u)\cdot u'$

Ancak bu durumda bir bileşik fonksiyon türetmeliyiz, çünkü sekant üçüncü kuvvete yükseltilmiştir ve ayrıca argümanında bir polinom fonksiyonumuz vardır. Dolayısıyla, tüm fonksiyonun türevini almak için zincir kuralını uygulamamız gerekir:

$\begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}$

Bir sekantın türevine ilişkin çözülmüş alıştırmalar

Aşağıdaki sekant fonksiyonlarını türetin:

$\text{A) }f(x)=\text{sec}(x^6-6x^3)$

$\text{B) }f(x)=\text{sec}^4(5x^4)$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)$

Çözümü görün

$\text{A) }f(x)=\text{sec}(x^6-6x^3)\cdot \text{tan}(x^6-6x^3)\cdot (6x^5-18x^2)$

$\begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}$

$\text{C) }f(x)=\text{sec}\bigl(\ln(x)\bigr)\cdot \text{tan}\bigl(\ln(x)\bigr)\cdot \cfrac{1}{x}$

$\text{D) }f(x)=\text{sec}\left(e^{x^2+3x}\right)\cdot \text{tan}\left(e^{x^2+3x}\right)\cdot e^{x^2+3x}\cdot (2x+3)$

$\text{E) }f(x)=\text{sec}\left(\sqrt{5x+1}\right)\cdot \text{tan}\left(\sqrt{5x+1}\right)\cdot \cfrac{5}{2\sqrt{5x+1}}$

Sekantın türevinin formülünün gösterilmesi

Daha sonra sekantın türevinin formülünü ispatlayacağız. Kanıtı ezbere bilmek elbette gerekli olmasa da formüllerin nereden geldiğini anlamak her zaman iyidir.

Matematiksel olarak sekantın tanımı kosinüsün çarpımsal tersidir:

$f(x)=\text{sec}(x)=\cfrac{1}{\text{cos}(x)}$

Bu nedenle bölüm kuralını kullanarak sekantı türetmeyi deneyebiliriz:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}^2(x)}$

Ve ilk bölümde gördüğümüz gibi, önceki ifade sekantın türevinin formülüne dönüştürülebilir. Bunu yapmak için kesri iki farklı kesre ayırıyoruz:

$f'(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}\cdot \cfrac{1}{\text{cos}(x)}$

Sinüs’ün kosinüs’e bölümü tanjanta eşdeğerdir, dolayısıyla söz konusu bölümü tanjantla değiştiririz:

$f'(x)=\text{tan}(x)\cdot \cfrac{1}{\text{cos}(x)}$

Sekant fonksiyonunun matematiksel tanımına göre kosinüs, bunun ters çarpımıdır. Yani kosinüse bölünen sayının sekant ile değiştirilmesiyle türevinin formülüne ulaşıyoruz:

$f'(x)=\text{tan}(x)\cdot \text{sec}(x)$

Sekantın türevi nedir?

Sekantın türevine örnekler

Örnek 1: 2x’in sekantının türevi

Örnek 2: x karenin sekantının türevi

Örnek 3: Bir polinomun sekant küpünün türevi

Bir sekantın türevine ilişkin çözülmüş alıştırmalar

Sekantın türevinin formülünün gösterilmesi

Yorum bırakın Yanıtı iptal et