Teğet çizgi denklemi -

Bu yazıda bir eğriye teğet denkleminin nasıl bulunacağını göreceğiz. Ayrıca farklı zorluk seviyelerindeki çözümlü alıştırmalarla antrenman yapabilirsiniz.

Bir noktadaki bir fonksiyona teğet doğrunun denklemi

f(x) fonksiyonuna x=x ₀ noktasındaki teğetin denklemi :

$y -y_0= m(x-x_0)$

P(x ₀ ,y ₀ ) noktası, teğet ile fonksiyonun çakıştığı noktadır. Ve teğetin eğimi m, eğrinin x ₀ noktasındaki türevine eşittir, yani m=f'(x ₀ ).

Yukarıdaki resimde bir eğri görebilirsiniz

$f(x)$

maviyle ve fonksiyona teğet turuncu bir çizgiyle temsil edilir

$f(x)$

Hakkında

$x=x_0$

çünkü sadece bu ortak noktaları var. Peki, bu teğetin denklemi

$y -y_0= m(x-x_0)$

ve eğimi

$m=f'(x_0)$

Teğet denklemi nasıl bulunur?

Bir noktadaki fonksiyona teğet denklemini bulmak için yapmanız gerekenler:

Fonksiyonun teğet noktasındaki türevini hesaplayarak teğet doğrunun eğimini bulun.
Teğet doğrusu üzerinde bir nokta belirleyin.
Hesaplanan eğimi ve teğet doğrunun noktasını kullanarak teğet doğrunun denklemini bulun .

Bir eğriye teğet denklemi örneği

Teğet denkleminin teorisini gördükten sonra, bir örneği adım adım çözerek teğet denkleminin nasıl hesaplanacağını görelim:

Eğrinin teğet denklemini hesaplayın
$f(x)=x^2+x$

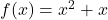
Hakkında

$x=1$

.

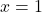
Teğet denkleminin her zaman aşağıdaki biçimde olduğunu biliyoruz:

$y -y_0= m(x-x_0)$

Yapılacak ilk şey çizginin eğimini hesaplamaktır. Böylece teğetin eğimi,

$m$

, eğrinin x=1 teğet noktasındaki türevinin değeri olacaktır, yani

$m=f'(1).$

Bu nedenle fonksiyonun türevini alıyoruz ve sonra hesaplıyoruz

$f'(1):$

$f(x)=x^2+x \quad \longrightarrow \quad f'(x)=2x+1$

$f'(1)= 2\cdot 1+1=2+1=3$

$m=f'(1)=3$

Kıymetini bildiğimizde

$m$

bir nokta bulmamız lazım

$(x_0,y_0)$

Teğet doğru denklemini tamamlamak için teğet doğrunun

Teğet ve eğri denkleminin her zaman ortak bir noktası vardır ; bu durumda bu nokta

$x=1$

. Bu nedenle eğri gibi

$f(x)$

bu noktadan geçiyorsa noktanın diğer bileşenini hesaplayarak bulabiliriz.

$f(1):$

$f(x)=x^2+x$

$f(1)=1^2+1=2$

Dolayısıyla teğet nokta şudur:

$P(1,2)$

Hem eğri hem de teğet bu noktadan geçtiği için bunu teğetin denklemini bulmak için de kullanabiliriz.

Geriye kalan tek şey eğimin bulunan değerlerini ve teğet noktasını denkleminde değiştirmektir:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)$

Kısaca teğet denklem şu şekildedir:

$\bm{y-2=3(x-1)}$

Teğet doğrunun denklemini, doğrunun açık denklemiyle de ifade edebilirsiniz:

$\bm{y=3x-1}$

Aşağıda temsil edilen eğriyi görebilirsiniz

$f(x)=x^2+x$

ve ona teğet olan çizgi

$x=1,$

$y-2=3(x-1):$

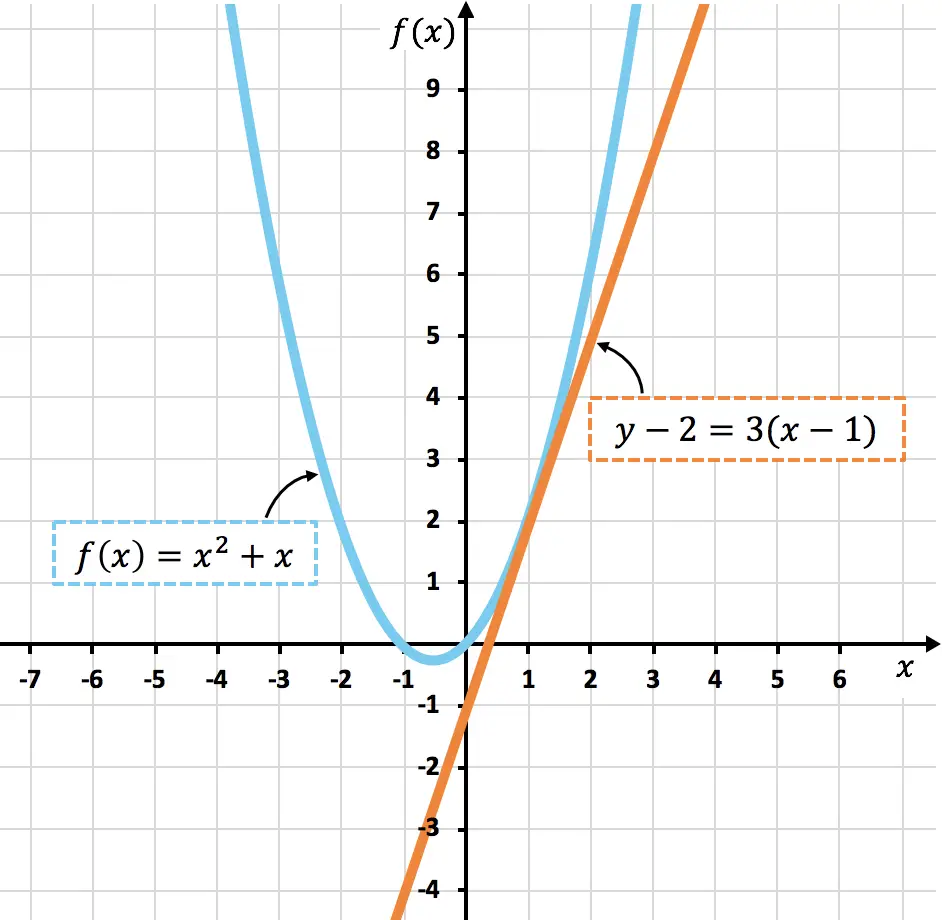
bir noktadaki bir eğriye teğet doğrunun denklemi

Gördüğünüz gibi eğri

$f(x)=x^2+x$

ve teğet

$y-2=3(x-1)$

sadece ortak noktaları var

$(1,2)$

tam olarak hesapladığımız gibi.

Teğet denklemle ilgili çözülmüş alıştırmalar

1. Egzersiz

Eğrinin teğet denklemini hesaplayın

$f(x)=2x^2-4x+3$

Hakkında

$x=2 .$

Çözümü görün

Teğet denklemi her zaman aşağıdaki biçimde olacaktır:

$y-y_0=m(x-x_0)$

Adım 1: Teğet doğrunun eğimini hesaplayın

Eğim, m , eğrinin teğetlik noktasındaki türevinin değeridir. Bu nedenle bu durumda

$m = f'(2):$

$f(x)=2x^2-4x+3 \ \longrightarrow \ f'(x)= 4x-4$

$f'(2)= 4\cdot 2-4=8-4=4$

$m=f'(2)=4$

Adım 2: Teğet doğrusu üzerinde bir nokta bulun

Teğet ve eğri denkleminin her zaman ortak bir noktası vardır; bu durumda bu nokta

$x=2$

. Bu nedenle eğri gibi

$f(x)$

bu noktadan geçiyorsa noktanın diğer bileşenini hesaplayarak bulabiliriz.

$f(2):$

$f(x)=2x^2-4x+3$

$f(2)=2\cdot 2^2-4\cdot 2+3 =2 \cdot 4 -8 +3 = 3$

Böylece hem eğrinin hem de teğetin geçtiği nokta noktadır.

$(2,3).$

Adım 3: Teğet denklemini yazın

Geriye kalan tek şey eğimin bulunan değerlerini ve teğet noktasını denkleminde değiştirmektir:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)$

Bu nedenle teğet denklem şu şekildedir:

$\bm{y -3= 4(x-2)}$

Alıştırma 2

Eğrinin teğet denklemini hesaplayın

$\displaystyle f(x)=-3x^2+2x$

koordinatların başlangıç noktasında.

Çözümü görün

Koordinatların orijini noktayı ifade eder

$(0,0).$

Bu nedenle fonksiyona bu noktada teğetini hesaplamamız gerekir.

$(0,0) .$

Öncelikle koordinatların orijinindeki türevi hesaplayarak teğetin eğiminin değerini belirliyoruz:

$f(x)=-3x^2+2x \ \longrightarrow \ f'(x)= -6x+2$

$f'(0)= -6\cdot 0+2=2$

$m=f'(0)=2$

Bu durumda teğetin geçtiği noktayı zaten biliyoruz. Çünkü ifade bize doğrunun koordinatların orijininde yani noktada eğriye teğet olması gerektiğini söylüyor.

$(0,0).$

Yani eğri ile teğetin paylaştığı nokta noktadır

$(0,0).$

Son olarak eğim ve teğet noktası için bulunan değerleri denkleminizde değiştirin:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)$

Sonuç olarak teğet denklem şu şekildedir:

$y -0= 2(x-0)$

$\bm{y = 2x}$

Alıştırma 3

Eğriye teğet çizgiyi hesaplayın

$f(x)=x^2-2x-1$

sağa paralel olan

$y-4x-6=0$

Çözümü görün

Bu problemde bize teğetin doğruya paralel olması gerektiği söylendi.

$y-4x-6=0 .$

Ve eğer eğimleri aynıysa iki doğru paraleldir. Bu nedenle teğetin doğru ile aynı eğime sahip olması gerekir

$y-4x-6=0.$

Bu, doğrunun eğimini bulmamız gerektiği anlamına gelir.

$y-4x-6=0 .$

Bunu yapmak için değişkeni temizliyoruz ve:

$y-4x-6=0 \ \longrightarrow \ y =4x+6$

Yani doğrunun eğimi

$y=4x+5$

4’tür, çünkü bir doğrunun eğimi, y net olduğunda x’i çarpan sayıdır.

Bu nedenle teğetin eğiminin de 4 olması gerekir çünkü paralel olmaları için eğimlerinin aynı olması gerekir.

$m=4$

Bu durumda bize eğri ile teğet arasındaki teğet noktayı söylemezler. Ancak eğrinin teğet noktasındaki türevinin teğetin eğimine eşit olduğunu biliyoruz, yani

$m=f'(x_0)$

. Peki değerini nasıl bilebiliriz?

$m$

denklemden x _0’ı bulabiliriz

$m=f'(x_0):$

Bunu yapmak için önce türevini hesaplıyoruz.

$f(x):$

$f(x)= x^2-2x-1 \ \longrightarrow \ f'(x)=2x-2$

Ve şimdi çözüyoruz

$m=f'(x_0)$

bilerek

$m = 4 :$

$m =f'(x_0)$

$4 =2(x_0)-2$

$4+2 =2x_0$

$6 =2x_0$

$\cfrac{6}{2} =x_0$

$3=x_0$

Noktanın x koordinatını bildiğimizde noktanın diğer koordinatını hesaplayarak bulabiliriz.

$f(3):$

$f(3)=3^2-2\cdot 3-1= 9-6-1=2$

Böylece hem eğrinin hem de teğetin geçtiği nokta noktadır.

$(3,2).$

Geriye kalan tek şey eğimin bulunan değerlerini ve teğet noktasını denkleminde değiştirmektir:

$\left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)$

Ve teğetin denklemi:

$\bm{y -2=4(x-3)}$

Alıştırma 4

Eğriye teğet çizgiyi hesaplayın

$f(x)=2x^2+5x+1$

X ekseni ile 45°’lik bir açı oluşturur.

Çözümü görün

Problem ifadesi bize teğet doğrunun X ekseniyle 45°’lik bir açı oluşturması gerektiğini söylüyor. Bu durumlarda eğim değerini bulmak için aşağıdaki formülün uygulanması gerekir:

$m = \text{tg}\left(\alpha\right)$

$m = \text{tg}\left(45^{\text{o}}\right) = 1$

İfade, eğri ile teğet çizgisi arasındaki teğetlik noktasını belirtmez. Ancak eğrinin teğet noktasındaki türevinin teğetin eğimine eşdeğer olduğunu biliyoruz, yani

$m=f'(x_0)$

. Bu nedenle denklemi çözerek x _0’ı hesaplayabiliriz.

$m=f'(x_0):$

Bunu yapmak için önce türevini hesaplıyoruz.

$f(x):$

$f(x)=2x^2+5x+1\ \longrightarrow \ f'(x)=4x+5$