Burada bir fonksiyonun hiperbolik arksekantının türevini nasıl hesaplayacağınızı bulacaksınız. Ek olarak hiperbolik arksekantın türevinin çözülmüş örneklerini görebileceksiniz.
Hiperbolik arksekant türevi formülü
X’in hiperbolik arksekantının türevi, negatif 1 bölü x çarpı birin kökü eksi x karenin çarpımına eşittir.
![]()
Bu nedenle, bir fonksiyonun hiperbolik arksekantının türevi, eksi bu fonksiyonun türevinin, fonksiyonun çarpımının çarpı birin kökü eksi kare fonksiyonuna bölümüdür.
![]()
Kısaca hiperbolik arksekant fonksiyonunun türevinin formülü şöyledir:
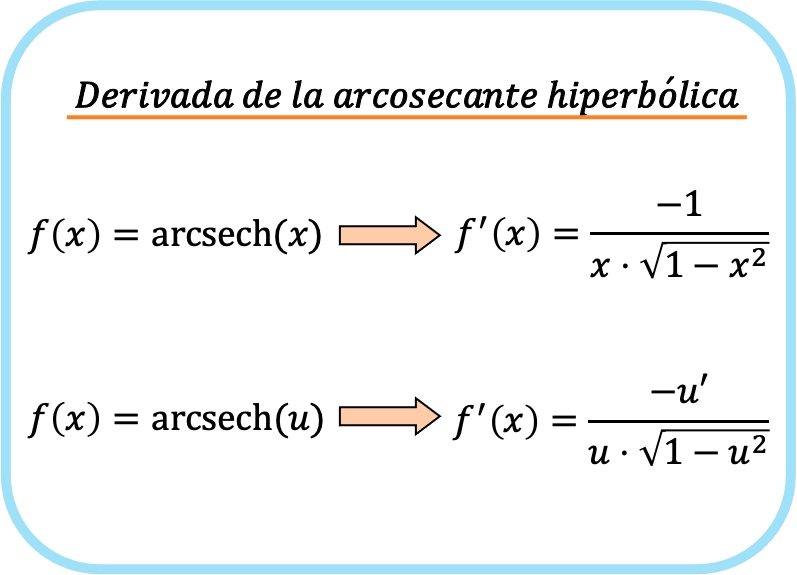
Her iki ifade de aslında aynı formüle karşılık gelir ancak ikinci formüle zincir kuralı uygulanır. Aslında u yerine x özdeşlik fonksiyonunu koyarsanız x’in türevi 1 olduğundan ilk formülü elde edersiniz.
Hiperbolik arksekantın türevi örnekleri
Hiperbolik yaysekantın türevinin formülünün ne olduğunu gördükten sonra, bu tür ters trigonometrik türevlerin iki adım adım alıştırmasını çözeceğiz. Böylece bir fonksiyonun hiperbolik arksekantının nasıl elde edildiğini tam olarak görebilirsiniz.
örnek 1
Bu örnekte 2x hiperbolik arksekantın türevinin ne olduğunu belirleyeceğiz.
![]()
Hiperbolik arksekant argümanında, x dışında bir fonksiyonumuz var, dolayısıyla bunu türetmek için zincir kuralı formülünü kullanmamız gerekiyor:
![]()
2x fonksiyonu doğrusal olduğundan türevi 2’dir. Bu nedenle, türevi bulmak için formülde u yerine 2x ve u’ yerine 2 koyarız:
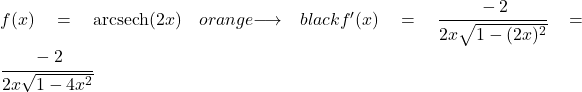
Örnek 2
Bu ikinci alıştırmada, bir polinom fonksiyonunun hiperbolik yaysekantını türeteceğiz:
![]()
Bu alıştırmanın işlevi bileşiktir çünkü hiperbolik arksekantın argümanında başka bir işlevi vardır. Dolayısıyla, türetilmesini gerçekleştirmek için hiperbolik arksekant türev formülünü zincir kuralıyla birlikte kullanmamız gerekir:
![]()
Bu nedenle, kesrin payına argümanın polinom fonksiyonunun türevini koyuyoruz ve paydada u’yu polinom fonksiyonuna göre değiştiriyoruz:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)
Benzer ürünler
- Hiperbolik sekant türevi
- Hiperbolik arksinüs türevi
- Hiperbolik sinüsün türevi
- Arsekant türevi
- sekantın türevi
- arksinüs türevi
- sinüsten türetilmiş