Burada bir fonksiyonun hiperbolik kotanjantının nasıl elde edileceğini açıklıyoruz. Ayrıca hiperbolik kotanjantın türevinin örneklerini de bulacaksınız.
Hiperbolik kotanjantın türevinin formülü
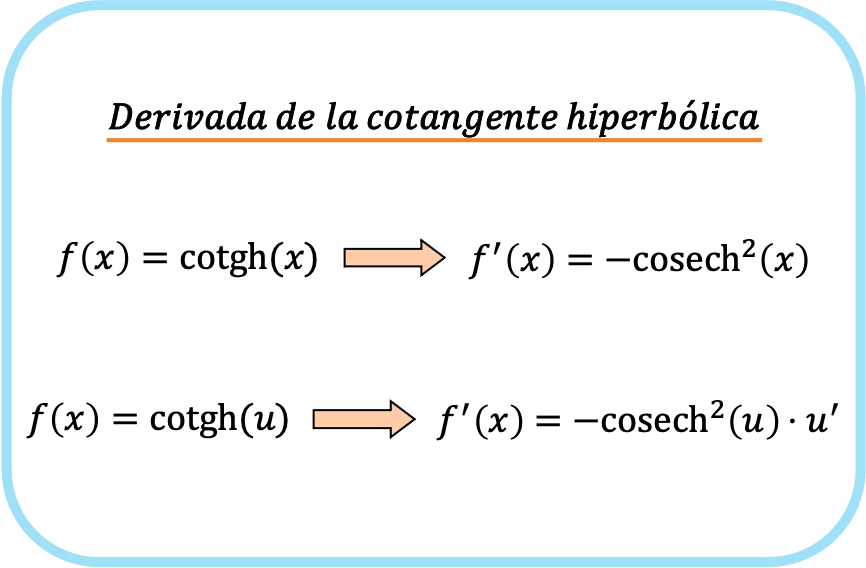
X’in hiperbolik kosekantının türevi eksi x karenin hiperbolik kosekantına eşittir.
![]()
Bu nedenle, bir fonksiyonun hiperbolik kotanjantının türevi eksi fonksiyonun hiperbolik kosekantı çarpı o fonksiyonun türevidir.
![]()
İkinci formülde zincir kuralının uygulandığını ve hiperbolik kotanjant argümanında x dışında bir fonksiyon olduğunda bu formülün kullanıldığını unutmayın.
Aşağıdaki üç ifade eşdeğer olduğundan, bazı matematik kitaplarında kotanjantın türevinin başka bir şey olduğunu görebilirsiniz:
![]()
Açıkçası, hiperbolik kotanjantı türetmek için bu üç ifadeden hangisini tercih ederseniz onu kullanabilirsiniz, ancak en çok kullanılanı hiperbolik kosekantın karesidir.
Hiperbolik kotanjantın türevi örnekleri
Bir fonksiyonun hiperbolik kotanjantının türevinin formülünün ne olduğunu öğrendikten sonra, bu tür trigonometrik türevlerin birkaç örneğini çözeceğiz.
örnek 1
Bu örnekte 2x fonksiyonunun hiperbolik kotanjantının türevinin ne olduğunu göreceğiz.
![]()
Hiperbolik kotanjant argümanında x dışında bir fonksiyonumuz var, bu nedenle türetmeyi yapmak için zincir kuralını içeren formülü kullanmamız gerekiyor:
![]()
2x birinci dereceden bir terim olduğundan türevi 2’dir. Yani 2x’in hiperbolik kotanjantının türevini bulmak için hiperbolik kosekantın kare argümanına 2x’i koyup 2 ile çarpmamız yeterlidir.
![]()
Örnek 2
İkinci örnekte bir polinom fonksiyonunun hiperbolik kotanjantının türevinin değerini belirleyeceğiz.
![]()
Yukarıda gördüğümüz gibi bir fonksiyonun hiperbolik kotanjantını türetme kuralı şu şekildedir:
![]()
Dolayısıyla bu alıştırmanın hiperbolik kotanjantının türevi aşağıdaki gibi olacaktır:
![]()