▷ Zincir kuralı (türevler): çözülmüş alıştırmalar

Burada zincir kuralının ne olduğunu ve zincir kuralını kullanarak fonksiyonların nasıl türetileceğini öğreneceksiniz. Ayrıca, zincir kuralıyla çözülen türevlerin çeşitli örneklerini görebileceksiniz ve hatta zincir kuralını uygulayan türevler üzerinde adım adım çözülmüş alıştırmalar ile pratik yapabileceksiniz.

Zincir kuralı nedir?

Zincir kuralı bileşik fonksiyonları türetmek için kullanılan bir formüldür. Zincir kuralı, bir f(g(x)) bileşik fonksiyonunun türevinin , f'(g(x)) türevi ile g'(x) türevinin çarpımına eşit olduğunu belirtir.

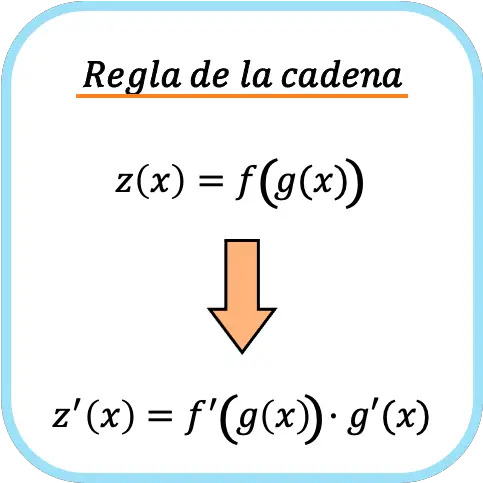
➤ Bakınız: bileşik fonksiyon

Gayri resmi olarak, zincir kuralının genellikle fonksiyonun türevini almak ve daha sonra onu içindekilerle çarpmak olduğu söylenir.

Zincir kuralı formülü, bileşik fonksiyonların türevini çok daha kolay bir şekilde almamızı sağlar, çünkü türev tanımının limitini kullanarak bir fonksiyonlar bileşiminin türevini alacak olsaydık, çok sayıda hesaplama yapmamız gerekirdi.

Öte yandan, bu kuralın herhangi bir fonksiyon tipi veya fonksiyonlu işlemler için değil, yalnızca bileşik fonksiyonların türevini bulmak için kullanıldığı dikkate alınmalıdır. Örneğin, çok yaygın bir hata, yanlış anlayıp zincir kuralını aşağıdaki gibi fonksiyonel ürünlere uygulamaktır:

$\ln(x)\cdot x^2$

❌

Zincir kuralı yalnızca bir işlevin diğerinin içinde olması durumunda kullanılabilir.

$\ln(x^2)$

✅

Zincir kuralına göre türev örnekleri

Zincir kuralının tanımı göz önüne alındığında, örnek olarak zincir kuralıyla çeşitli işlevler türeteceğiz. Bir örnekte fonksiyonun zincir kuralıyla nasıl türetildiğini anlamadıysanız, bunu bize yorumlarda sorabileceğinizi unutmayın!

örnek 1

Bu örnekte x karenin doğal logaritmasını elde etmek için zincir kuralını kullanacağız:

$f(x)=\ln(x^2)$

Doğal logaritmanın türevi argümanının 1 katına eşittir, dolayısıyla türev

$f'\bigl(g(x)\bigr)$

olmak:

$f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}$

$f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}$

Öte yandan x’in ikinin kuvvetine yükseltilmiş türevi 2x’tir:

$g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x$

Son olarak zincir kuralını uygulayarak tüm fonksiyonun türevini hesaplıyoruz. Bileşik fonksiyonun türevi az önce bulduğumuz iki türevin çarpımı olacaktır:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}$

Örnek 2

Bu ikinci örnekte polinoma dayalı bir potansiyel fonksiyon türeteceğiz:

$f(x)=\left(3x^2+4x-5\right)^3$

Bir kuvvet elde etmek için, orijinal üssü onun önüne koymamız ve üssün bir birimini çıkarmamız gerekir, böylece potansiyel fonksiyonun zincir kuralını uygulamadan türevi şöyle olur:

$f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2$

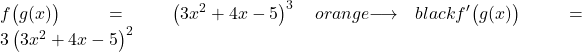
Şimdi parantez içindekileri çıkarıyoruz:

$g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4$

Ve son olarak, önceden hesaplanan iki türevin çarpımı olacak olan tüm fonksiyonun türevini çözmek için zincir kuralını kullanırız:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)$

Örnek 3

Bu durumda x küp artı 7x’in sinüs türevini çözeceğiz:

$f(x)=\text{sen}(x^3+7x)$

Aslında bu bir fonksiyonlar bileşimidir çünkü sinüs fonksiyonunun içinde x ³ +7x fonksiyonumuz vardır, dolayısıyla bileşik fonksiyonun türevini bulmak için zincir kuralını kullanabiliriz.

Bir yandan sinüsün türevi kosinüs olduğundan dış fonksiyonun türevi sinüsle aynı argümanla kosinüs olacaktır:

$f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)$

Öte yandan x ³ +7x’in türevi 3x ² +7’dir.

$g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7$

Bu nedenle bileşik fonksiyonun türevi iki türevin çarpımıdır:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)$

Zincir kuralıyla türevlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Zincir kuralını kullanarak aşağıdaki bileşik fonksiyonu türetin:

$f(x)=\left(5x^2-6x\right)^3$

Çözümü görün

Dış fonksiyon potansiyel bir fonksiyon olduğundan türevini hesaplamak için aşağıdaki formülü uygulamanız gerekir:

$f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}$

$f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2$

Daha sonra içerideki fonksiyonun türevini hesaplıyoruz. Bu, kuvvetlerin çıkarılmasıdır, dolayısıyla türevini hesaplamak için aşağıdaki formülü terimlerin her birine uygulamanız gerekir:

$f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}$

$g(x)=5x^2-6x\ \longrightarrow$

$g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6$

Kısacası bileşik fonksiyonun türevi, bulunan iki türevin çarpımıdır:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}$

Alıştırma 2

Aşağıdaki bileşik fonksiyonun türevini zincir kuralını kullanarak çözün:

$f(x)=-3\left(5x^5+9x^3\right)^4$

Çözümü görün

Öncelikle dış fonksiyonun türevini buluyoruz:

$\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}$

Şimdi iç fonksiyonun türevini çözüyoruz:

$g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2$

Dolayısıyla tüm fonksiyonun türevi şu şekildedir:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}$

Alıştırma 3

Aşağıdaki fonksiyon bileşiminin türevini zincir kuralıyla hesaplayın:

$f(x)=e^{2x^3}$

Çözümü görün

Bu üstel bir fonksiyon olduğundan türevini hesaplamak için aşağıdaki formülü uygulamanız gerekir:

$f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}$

$f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}$

Ayrıca fonksiyonu, fonksiyonun üssünden de ayırt ederiz:

$g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2$

Tamsayı bileşik fonksiyonunun türevini bulmak için zincir kuralını kullanırız:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}$

Alıştırma 4

Zincir kuralını kullanarak aşağıdaki bileşik fonksiyonun türevini bulun:

$f(x)=\sqrt[3]{\text{sen}(x) +x }$

Çözümü görün

Bu bir fonksiyonlar bileşimidir, çünkü irrasyonel bir fonksiyonun argümanında sinüzoidal bir fonksiyonumuz ve doğrusal bir fonksiyonumuz var. Önce kökün türevini hesaplıyoruz:

$f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

$f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}$

Ve şimdi argümanı radikalden türetiyoruz. Bu, fonksiyonların toplamı olduğundan türev, her terimin türevlerinin toplamı olacaktır:

$g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1$

Böylece tüm fonksiyonun türevi, hesaplanan iki türevin çarpımına eşittir:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}$

Alıştırma 5

Zincir kuralını kullanarak aşağıdaki fonksiyon bileşimini türetin:

$f(x)=3^{x^2+5}$

Çözümü görün

Zincir kuralını uygulamak için kuvvetin türevini ve polinomu bulup çarpmanız gerekir. Böylece ilgili formülü kullanarak gücü elde ederiz:

$f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)$

$f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)$

İkinci olarak polinom fonksiyonunu üstelden türetiyoruz:

$g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x$

Ve zincir kuralı bize tüm fonksiyonun türevinin az önce bulduğumuz türevlerin çarpımı olduğunu söyler:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}$

Alıştırma 6

$f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)$

Çözümü görün

Açıkçası, bu problemdeki fonksiyon bileşiktir, çünkü doğal logaritmanın argümanında iki farklı fonksiyon tipinin çarpımı vardır. İlk önce logaritmanın türevini alıyoruz:

$f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}$

$f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }$

İkinci olarak, fonksiyonu logaritma argümanından türetiyoruz. Bu, iki fonksiyonun çarpımıdır, dolayısıyla türetmeyi yapmak için aşağıdaki formülü kullanmanız gerekir:

$z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)$

$\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}$

Böylece, zincir kuralına göre tüm fonksiyonun türevi, iki türevin çarpımı olacaktır:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}$

Egzersiz 7

Aşağıdaki fonksiyonun türevini zincir kuralını kullanarak çözün:

$f(x)=\log_9 (e^{x^2}-6x^7)$

Çözümü görün

Bu bir fonksiyonlar bileşimidir, dolayısıyla logaritmanın ve argümanının türevini ayrı ayrı alacağız ve sonra türevleri çarpacağız.

Öncelikle logaritmanın 9 tabanına türevini alıyoruz:

$f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}$

$f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}$

Şimdi logaritmanın argümanının türevini hesaplıyoruz. e sayısının argümanında bir fonksiyon olduğuna dikkat edin, yani bu bir bileşik fonksiyondur, dolayısıyla bu fonksiyonu türetmek için zincir kuralını da uygulamamız gerekir:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x$

Böylece logaritmanın tamsayı argümanının türevi şöyle olacaktır:

$g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6$

Ve son olarak, tüm fonksiyonun türevi f'(g(x)) ile g'(x)’in çarpımı olacaktır:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}$

Egzersiz 8

Zincir kuralını kullanarak aşağıdaki bileşik fonksiyonu türetin:

$f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Çözümü görün

Bu alıştırmada çeşitli fonksiyonların birleşimine sahibiz, dolayısıyla zincir kuralını birkaç kez uygulamamız gerekecek. İlk olarak trigonometrik fonksiyonu türevi kosinüs olan sinüsten türetiyoruz:

$f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Şimdi zincir kuralını kullanarak sinüs argümanının türevini hesaplıyoruz:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}$

Son olarak, zincir kuralını tekrar uygulayarak fonksiyonların tüm bileşiminin türevini elde ederiz:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}$

Zincir Kuralı Kanıtı

Son olarak zincir kuralı formülünü ispatlayacağız. Bunu yapmak için türevin matematiksel tanımından başlayacağız:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

z iki fonksiyondan oluşan bir fonksiyon olsun:

$z=f\bigl(g(x)\bigr)$

O halde tanımı uygulayan z fonksiyonunun türevi şöyle olacaktır:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}$

Bildiğiniz gibi bir kesri aynı terimle çarpabilir ve bölebilirsiniz çünkü bu sonucu değiştirmez. Bu nedenle bir sonraki adıma geçebiliriz:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}$

Kesirlerin paydalarını yeniden düzenliyoruz:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}$

Limit özelliklerini uygulayarak yukarıdaki limiti ikiye bölebiliriz. Bir ürünün limiti limitlerin çarpımına eşit olduğundan:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Ve bu ifade aşağıdakine eşdeğerdir:

$\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

Türevin tanımından ona ulaştığımız için zincir kuralı formülü bu nedenle kanıtlanmıştır.

Zincir kuralı nedir?

Zincir kuralına göre türev örnekleri

örnek 1

Örnek 2

Örnek 3

Zincir kuralıyla türevlerle ilgili çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Egzersiz 7

Egzersiz 8

Zincir Kuralı Kanıtı

Yorum bırakın Yanıtı iptal et