Bu makalede bir fonksiyonun hiperbolik kosekantının nasıl elde edileceğini açıklıyoruz. Ek olarak hiperbolik kosekantın türevinin birkaç çözülmüş örneğini görebileceksiniz.
Hiperbolik kosekantın türevinin formülü
X’in hiperbolik kosekantının türevi eksi x’in hiperbolik kosekantı çarpı x’in hiperbolik kosekantı eşittir.
![]()
Bu nedenle, bir fonksiyonun hiperbolik kosekantının türevi eksi fonksiyonun hiperbolik kosekantının çarpımı çarpı fonksiyonun hiperbolik kosekantı çarpı adı geçen fonksiyonun türevidir.
![]()
Kısaca, bir fonksiyonun kosekantını türetme formülü şöyledir:
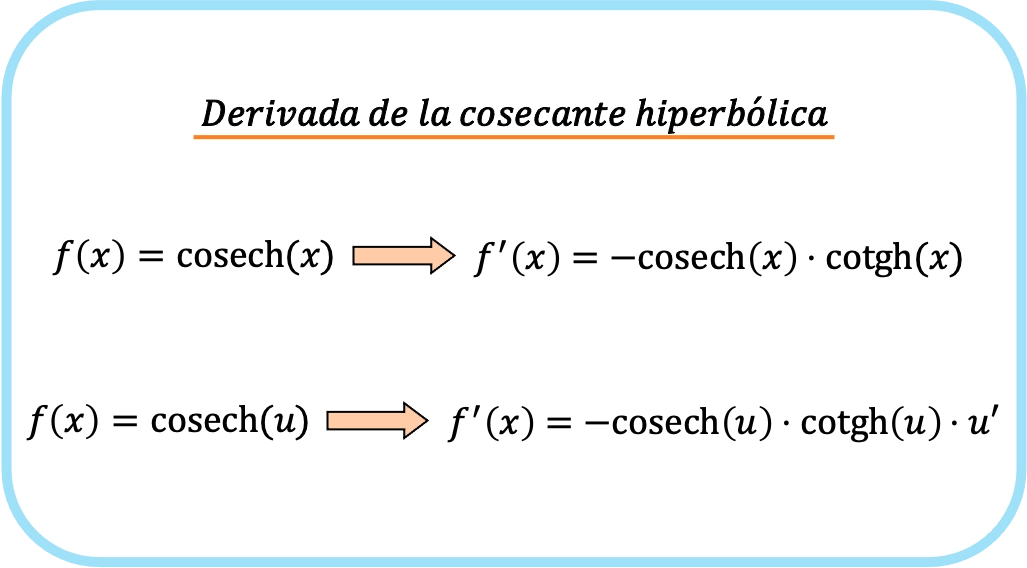
Aslında önceki iki ifade tek bir formüle karşılık gelmektedir, fark ikinci formülde zincir kuralının uygulanmasıdır.
Hiperbolik kosekantın türevi örnekleri
Hiperbolik kosekantın türevinin formülünün ne olduğunu gördükten sonra, bu tür trigonometrik türevin çalışılmış birkaç örneğini burada bulabilirsiniz.
örnek 1
Bu ilk örnekte x karenin hiperbolik kosekantını türeteceğiz:
![]()
Hiperbolik kosekantın bağımsız değişkeninin işlevi x’ten farklıdır, bu nedenle hiperbolik kosekantın türevi için zincir kuralına sahip formülü kullanmamız gerekir.
![]()
Yani, bu trigonometrik fonksiyonu türetmek için, önceki formüldeki değerleri yerine koymalıyız, yani hiperbolik kosekant ve hiperbolik tanjant argümanında x 2’yi koyarız ve hepsini türevle çarparız. x kare, yani 2x:
![]()
Örnek 2
Bu alıştırmada x küpün hiperbolik kosekantının türevinin ne kadar olduğunu göreceğiz:
![]()
Bir fonksiyonun hiperbolik kosekantının türevini bulmak için formülünü uygularız:
![]()
x küp’ün türevi 3x 2’dir , yani tüm fonksiyonun türevi:
![]()