Bu makalede bir fonksiyonun hiperbolik sekantının nasıl elde edileceğini açıklıyoruz. Hiperbolik sekantın türevinin formülünü ve bu türevin çalışılmış birkaç örneğini bulacaksınız.
Hiperbolik sekantın türevinin formülü
X’in hiperbolik sekantının türevi eksi x’in hiperbolik sekantının çarpımının x’in hiperbolik tanjantının çarpımına eşittir.
![]()
Bu nedenle, bir fonksiyonun hiperbolik sekantının türevi eksi fonksiyonun hiperbolik sekantının çarpımı çarpı fonksiyonun hiperbolik tanjantı çarpı adı geçen fonksiyonun türevidir.
![]()
Kısaca hiperbolik sekant fonksiyonunun türevinin formülü şöyledir:
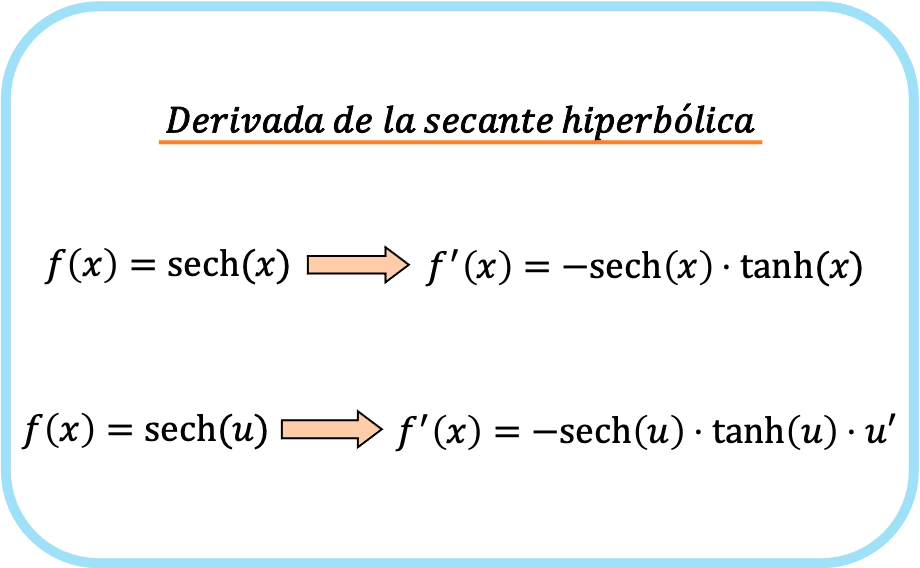
Her iki ifadenin de aslında tek bir formüle ait olduğunu unutmayın. Tek fark ikinci formülde zincir kuralının uygulanmasıdır.
Hiperbolik sekantın türevi örnekleri
Artık hiperbolik sekantın türevinin formülünü bildiğimize göre, bu tür trigonometrik türevin çözülmüş birkaç alıştırmasını göreceğiz.
örnek 1
![]()
Bu örnekte hiperbolik sekant argümanında x’ten farklı bir fonksiyonumuz var, dolayısıyla bunu türetmek için zincir kuralı formülünü kullanmamız gerekiyor.
![]()
2x fonksiyonu doğrusal olduğundan türevi 2’dir. Bu nedenle, türevi bulmak için formülde u’yu 2x ile ve u”yu 2 ile değiştiririz:
![]()
Örnek 2
![]()
Bu alıştırmanın işlevi bileşiktir, çünkü hiperbolik sekantın argümanında başka bir işlevi vardır. Bu nedenle, türetilmesini sağlamak için hiperbolik sekant formülünü zincir kuralıyla birlikte kullanmalıyız:
![]()
x’in 2’ye yükseltilmiş türevi 2x’i verir, dolayısıyla x karenin hiperbolik sekantının türevi şöyle olur:
![]()