Kosekantın türevi

Bu makalede bir fonksiyonun (formülün) kosekantının nasıl türetileceğini açıklıyoruz. Ayrıca kosekantın türevi için adım adım çözülmüş alıştırmalar da bulacaksınız. Ve son olarak, bu tip trigonometrik türevin formülünün gösterimini görebileceksiniz.

Kosekant türevi formülü

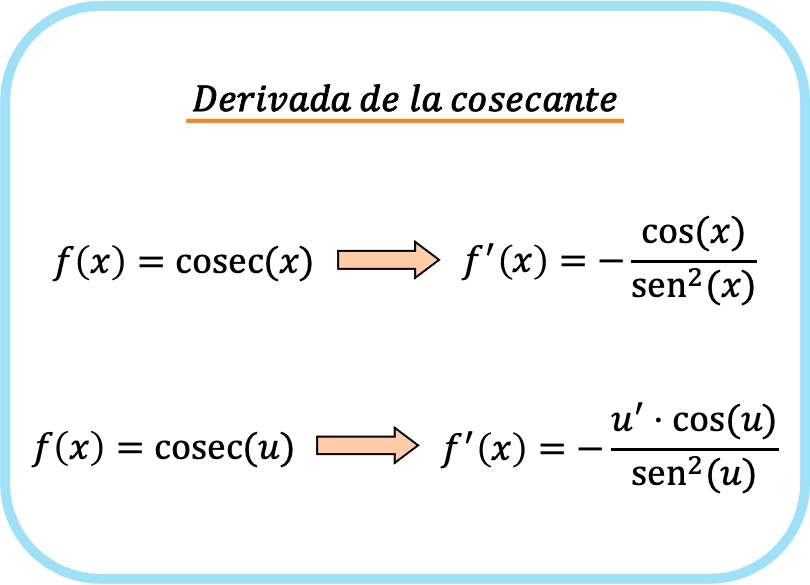
X’in kosekantının türevi, eksi x’in kosinüsünün bölümünün sinüs x’in karesine bölünmesine eşittir.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

Trigonometrik formülleri kullanarak, x’in kosekantının türevini eksi x’in kosekantının çarpı x’in kosekantının çarpımı olarak da tanımlayabiliriz.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

Ve eğer zincir kuralını uygularsak, bir fonksiyonun kosekantının türevi eksi fonksiyonun türevi çarpı fonksiyonun kosinüsünün çarpımı, fonksiyonun kare sinüsüne bölünür.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Dolayısıyla bir fonksiyonun kosekantını türetmek için kullanılan formül aşağıdaki gibidir:

Kosekantın türevine örnekler

Kosekantın türevinin formülünü gördükten sonra şimdi birkaç örnek vereceğiz. Böylece bir fonksiyonun kosekantının tam olarak nasıl türetildiğini görebilirsiniz.

Örnek 1: 2x kosekantının türevi

Bu örnekte 2x’in kosekantının türevinin ne kadar olduğunu göreceğiz:

$f(x)=\text{cosec}(2x)$

Kosekant argüman fonksiyonu x’ten farklıdır, dolayısıyla kosekant türev kuralını zincir kuralıyla birlikte kullanmamız gerekir.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Dolayısıyla, bu trigonometrik fonksiyonun türevini bulmak için, önceki formüldeki değerleri değiştirmeniz yeterlidir: kosinüs ve sinüs argümanına 2x koyarız ve u’, 2x’in türevine, yani 2’ye karşılık gelir:

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

Örnek 2: x karenin kosekantının türevi

Bu alıştırmada x karenin kosekantının türevinin ne kadar olduğunu göreceğiz:

$f(x)=\text{cosec}(x^2)$

Mantıksal olarak bu trigonometrik fonksiyonun türevi, kosekantın türevinin formülü kullanılarak çözülür:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

x karenin türevi 2x’i verir, dolayısıyla x’in ikinci kuvvetinin kosekantının türevi şöyle olur:

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

Örnek 3: Üstel bir fonksiyonun kübik kosekantının türevi

$f(x)=\text{cosec}^3(e^{5x})$

Fonksiyonun argümanı ne olursa olsun, bir fonksiyonun kosekantının türevine ilişkin kural şudur:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Ancak bu durumda bileşik bir fonksiyonumuz var çünkü kosekant üçe yükseltildi ve dahası argümanında üstel bir fonksiyon var. Dolayısıyla, fonksiyonun tamamının türevini almak için zincir kuralını birkaç kez uygulamamız gerekir:

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

Kosekantın türevinin çözülmüş problemleri

Aşağıdaki kosekant fonksiyonlarını türetin:

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

Çözüme bakın

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

Kosekantın türevinin formülünün kanıtı

Daha sonra kosekantın türevinin formülünü göstereceğiz. Diğer gösterilerden farklı olarak bu durumda türevi tanımlayan limiti kullanmayacağız, ancak kosekantın matematiksel tanımından başlayacağız.

Cebirsel olarak kosekant trigonometrik fonksiyon sinüsün çarpımsal tersidir:

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

Bu nedenle bölüm kuralını kullanarak kosekantın türevini alabiliriz:

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

Gördüğünüz gibi, kosekantın türevinin formülüne ancak bölümün türevi kuralını uygulayarak ulaşıyoruz. Ve bir bölümün türevi zaten kanıtlanmış olduğundan (bunu aşağıdaki bağlantıda görebilirsiniz), kosekant türev kuralı da kanıtlanmış olur.

➤ Bakınız: bir bölümün türevinin kanıtı

Kosekant türevi formülü

Kosekantın türevine örnekler

Örnek 1: 2x kosekantının türevi

Örnek 2: x karenin kosekantının türevi

Örnek 3: Üstel bir fonksiyonun kübik kosekantının türevi

Kosekantın türevinin çözülmüş problemleri

Kosekantın türevinin formülünün kanıtı

Yorum bırakın Yanıtı iptal et