Hiperbolik arktanjantın türevi

Burada bir fonksiyonun hiperbolik arktanjantını nasıl türeteceğinizi bulacaksınız. Ayrıca bu tip trigonometrik türevlerin çözülmüş örneklerini de görebileceksiniz ve son olarak size hiperbolik arktanjantın türevinin formülünü göstereceğiz.

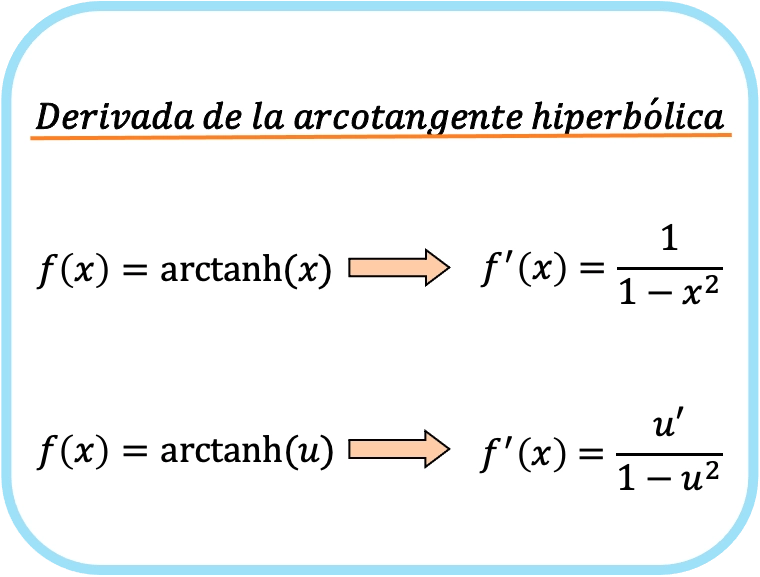
Hiperbolik arktanjantın türevinin formülü

X’in hiperbolik arktanjantının türevi bir bölü bir eksi x’in karesidir.

f(x)=\text{arctanh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}

Bu nedenle, bir fonksiyonun hiperbolik arktanjantının türevi, o fonksiyonun türevinin bir eksi adı geçen fonksiyonun karesine bölünmesine eşittir.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

Aslında her iki formül de aynıdır ancak ikincisinde zincir kuralı uygulanır. Örneğin, x’i u ile değiştirmek bize tam olarak ilk formülü verir, çünkü x’in türevi 1’dir.

hiperbolik arktanjantın türevi

Arktanjantın tanjantın ters fonksiyonu olması gibi, hiperbolik arktanjant da hiperbolik tanjantın tersidir. Öyle bile olsa türevleri çok farklı, bu trigonometrik fonksiyonun türevini buradan kontrol edebilirsiniz:

➤ Bakınız: hiperbolik tanjantın türevinin formülü

Hiperbolik arktanjant türevi örnekleri

örnek 1

f(x)=\text{arctanh}(2x)

Mantıksal olarak hiperbolik arktanjantın türevi kuralını uygulamamız gerekir:

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

2x’in türevi 2’dir, dolayısıyla kesrin payına iki, paydasına da bir eksi 2x kare koyun:

f(x)=\text{arctanh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1-(2x)^2}}=\cfrac{2}{1- 4x^2}

Örnek 2

f(x)=\text{arctanh}(e^{3x})

Bu fonksiyonun türevini çözmek için hiperbolik arktanjantın türevinin formülünü kullanmamız gerekir.

f(x)=\text{arctanh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

Ek olarak, hiperbolik arktanjant argüman fonksiyonu bileşik bir fonksiyon olduğundan zincir kuralını da uygulamamız gerekecek:

f(x)=\text{arctanh}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}

Hiperbolik arktanjantın türevinin kanıtı

Bu son bölümde hiperbolik arktanjantın türevinin formülünü göstereceğiz.

y=\text{arctanh}(x)

Hiperbolik arktanjant ters hiperbolik tanjant olduğundan önceki eşitliği başka bir şekilde ifade edebiliriz:

x=\text{tanh}(y)

Şimdi denklemin her iki tarafını da farklılaştırıyoruz:

1=\cfrac{1}{\text{cosh}^2(y)}\cdot y'

Sizi temizliyoruz:

y'=\text{cosh}^2(y)

Öte yandan hiperbolik kosinüs ile hiperbolik sinüsün kareleri farkının 1 verdiğini biliyoruz. Dolayısıyla önceki ifadeyi kesire dönüştürebiliriz:

\text{cosh}^2(y)-\text{senh}^2(y)=1

y'=\cfrac{\text{cosh}^2(y)}{1}=\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)-\text{senh}^2(y)}

Kesrin tüm terimlerini hiperbolik kosinüsün karesine böleriz:

y'=\cfrac{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}}{\cfrac{\text{cosh}^2(y)}{\text{cosh}^2(y)}-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

y'=\cfrac{1}{1-\cfrac{\text{senh}^2(y)}{\text{cosh}^2(y)}}

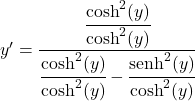
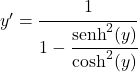
Hiperbolik sinüsün hiperbolik kosinüs arasındaki bölümü hiperbolik tanjanta eşittir, dolayısıyla:

\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}

y'=\cfrac{1}{1-\text{tanh}^2(y)}

Ancak ispatın başında gördüğümüz gibi, hiperbolik tanjant x değişkenine eşdeğerdir, dolayısıyla ifadeyi yerine koyarak hiperbolik yay tanjantının türevinin formülünü elde edebiliriz:

y'=\cfrac{1}{1-x^2}

Benzer ürünler

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top