Hiperbolik arksinüs türevi

Burada hiperbolik arksinüsün (formül) türevinin ne olduğunu bulacaksınız. Ek olarak, bir fonksiyonun hiperbolik arksinüsünün türevleri üzerine çözülmüş çeşitli alıştırmalar görebileceksiniz. Son olarak size bu tür trigonometrik fonksiyonların türevinin formülünü gösteriyoruz.

Hiperbolik arksinüs türevi formülü

X’in hiperbolik ark sinüsünün türevi, bir bölü x kare artı 1’in kareköküdür.

f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}

Yani bir fonksiyonun hiperbolik ark sinüsünün türevi, o fonksiyonun türevinin o fonksiyonun karekökünün karesi artı bire bölünmesine eşittir.

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

İkinci formül birinciye benzer ancak zincir kuralını uygular. Yani, birinci formülle yalnızca xy’nin hiperbolik arksinüsü türetilebilirken, ikinci formülle herhangi bir fonksiyonun hiperbolik arksinüsü türetilebilir.

hiperbolik arksinüsünden türetilmiştir

Hiperbolik arksinüsün, hiperbolik sinüsün ters fonksiyonu olduğunu unutmayın; bunun türevini burada görebilirsiniz:

➤ Bakınız: hiperbolik sinüsün türevinin formülü

Hiperbolik arksinüs türevi örnekleri

örnek 1

f(x)=\text{arcsenh}(3x)

Ark sinüs fonksiyonunun türevini çözmek için yukarıda görülen formülü kullanırız:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

3x’in türevi 3 olduğundan payda 3 vardır. Ve paydaya 3x kare artı 1’in karekökünü koymamız yeterli:

f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}

Örnek 2

f(x)=\text{arcsenh}(x^3)

x küp fonksiyonunun hiperbolik ark sinüsünü elde etmek için aynı formülü uygulamamız gerekir:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

x küpün türevi 3×2’dir , dolayısıyla x’in hiperbolik arksinüsünün 3’e yükseltilmiş türevi şöyle olacaktır:

f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}

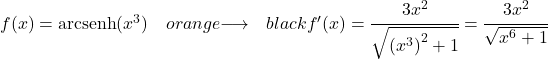
Hiperbolik arksinüs türevinin kanıtı

Hiperbolik arksinüsün türevinin formülünü göstereceğiz:

y=\text{arcsenh}(x)

Öncelikle hiperbolik ark sinüsünü hiperbolik sinüse dönüştürüyoruz:

x=\text{senh}(y)

Eşitliğin her iki tarafından da şunu çıkarıyoruz:

1=\text{cosh}(y)\cdot y'

Sizi temizliyoruz:

y'=\cfrac{1}{\text{cosh}(y)}

Daha sonra hiperbolik sinüs ile hiperbolik kosinüsü birbirine bağlayan trigonometrik özdeşliği uyguluyoruz:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}

y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}

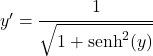
Ancak yukarıda x’in y’nin hiperbolik sinüsüne karşılık geldiğini çıkarmıştık, dolayısıyla denklem aynı kalıyor:

y'=\cfrac{1}{\sqrt{1+x^2}}

Gördüğünüz gibi bu adımları uygulayarak hiperbolik arksinüsün türevinin formülünü elde ettik, bu yüzden kanıtlanmıştır.

Benzer ürünler

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top