Hiperbolik tanjantın türevi

Burada bir fonksiyonun hiperbolik tanjantının türevinin ne olduğunu bulacaksınız. Ek olarak, hiperbolik teğetlerin türevlerinin birkaç çözülmüş örneğini görebileceksiniz. Ve son olarak size hiperbolik tanjantın türevinin formülünü gösteriyoruz.

Hiperbolik tanjantın türevinin formülü

X’in hiperbolik tanjantının türevi, 1’in x’in hiperbolik kosinüsünün karesine bölünmesine eşittir. X’in tanjantının türevi aynı zamanda x’in hiperbolik sekantının karesine ve 1 eksi x’in hiperbolik tanjantının karesine de eşdeğerdir.

$\begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}$

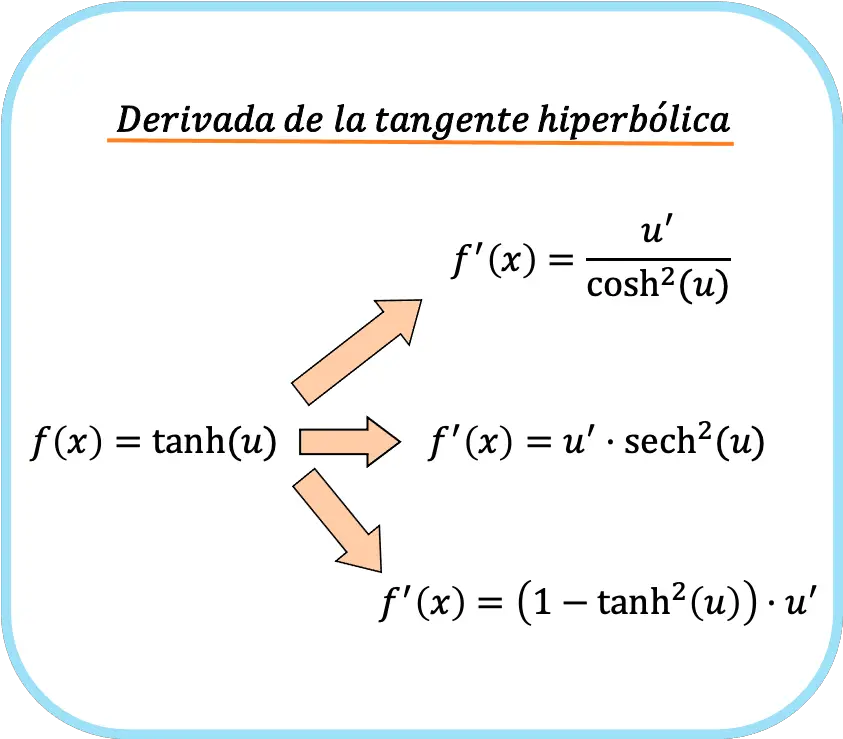
Öte yandan fonksiyon argümanında x dışında bir fonksiyonumuz varsa zincir kuralını uygulamamız gerekir. Ve hiperbolik tanjantın türevinin üç formülü şöyledir:

$\begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}$

Bu, hiperbolik tanjantı her türettiğimizde üç formülü de kullanmamız gerektiği anlamına gelmez, ancak onu türetmek için bunlardan herhangi birini kullanabileceğimiz anlamına gelir. Dolayısıyla hiperbolik tanjant argümanının işlevine bağlı olarak şu veya bu formülü kullanmak daha iyi olacaktır. Aşağıda bir fonksiyonun hiperbolik tanjantının nasıl türetildiğini görebileceğiniz birkaç örnek bulunmaktadır.

Hiperbolik tanjantın türevi, tanjantın türeviyle neredeyse aynıdır ancak onları tamamen farklı kılan küçük bir ayrıntıya sahiptir. Aşağıdaki bağlantıdan farkın ne olduğunu görebilirsiniz:

➤ Bakınız: teğet türev formülü

Hiperbolik tanjantın türevi örnekleri

Hiperbolik tanjantın türevinin formülünün ne olduğunu gördükten sonra, hiperbolik tanjantın nasıl türetileceğini tam olarak anlamanız için burada bu tür trigonometrik fonksiyonların türevlerinin çözülmüş birkaç örneğini bulacaksınız.

Örnek 1: 2x’in hiperbolik tanjantının türevi

$f(x)=\text{tanh}(2x)$

Bu örnekte hiperbolik tanjantı türetmek için hiperbolik kosinüs formülünü kullanacağız, ancak elbette hangisini tercih ederseniz onu kullanabilirsiniz.

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

2x’in türevinin 2 olduğunu biliyoruz, dolayısıyla tüm fonksiyonun türevi şöyle olur:

$f(x)=\text{tanh}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cosh}^2(2x)}$

Örnek 2: x karenin hiperbolik tanjantının türevi

$f(x)=\text{tanh}(x^2)$

Bir fonksiyonun hiperbolik tanjantının türevine ilişkin kural şöyledir:

$f(x)=\text{tanh}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cosh}^2(u)}$

Bir yandan, fonksiyonu, 2x’i veren x ² argümanından farklılaştırıyoruz ve ardından aşağıdaki formülü kullanarak tüm fonksiyonun türevini çözüyoruz:

$f(x)=\text{tanh}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cosh}^2(x^2)}$

Örnek 3: Hiperbolik tanjantın küp şeklinde türevi

$f(x)=\text{tanh}^3(7x^2)$

Bu durumda, üstelik bir kuvvete yükseltilmiş bir fonksiyonun hiperbolik tanjantını türetmemiz gerekir. Dolayısıyla potansiyel bir fonksiyonun türevi için formülü, hiperbolik tanjantın türevi kuralını ve zincir kuralını kullanmamız gerekir:

$f'(x)=3\text{tanh}^2(7x^2)\cdot \cfrac{14x}{\text{cosh}^2(7x^2)}}=\cfrac{42x\cdot \text{tanh}^2(7x^2)}{\text{cosh}^2(7x^2)}}$

Teğetin türevinin kanıtı

Bu bölümde hiperbolik tanjantın türevinin formülünü göstereceğiz. Bunun için de üç hiperbolik trigonometrik oranı birbirine bağlayan trigonometrik özdeşlikten başlayacağız:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

➤ Not: İspatı anlamak için hiperbolik sinüsün türevinin ne olduğunu ve hiperbolik kosinüsün türevinin ne olduğunu bilmeniz gerekir. Bu nedenle devam etmeden önce bağlantılı sayfaları ziyaret etmenizi öneririz.

Şimdi bir bölümün türevinin formülünü uygulayalım:

$\displaystyle\left(\text{tanh}(x)\right)'=\left(\frac{\text{senh}(x)}{\text{cosh}(x)}\right)'$

$\text{tanh}'(x)=\cfrac{\text{cosh}(x)\cdot \text{cosh}(x)-\text{senh}(x)\text{senh}(x) }{\text{cosh}^2(x)}$

$\text{tanh}'(x)=\cfrac{\text{cosh}^2(x)-\text{senh}^2(x)}{\text{cosh}^2(x)}$

Aşağıdaki formülü kullanarak kesrin payının ifadesini azaltıyoruz:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

$\text{tanh}'(x)=\cfrac{1}{\text{cosh}^2(x)}$

Gördüğünüz gibi önceki eşitlik hiperbolik tanjantın türevinin ilk formülüne karşılık geliyor. Benzer şekilde hiperbolik sekant, hiperbolik kosinüsün çarpımsal tersidir, dolayısıyla ikinci formül de türetilir:

$\text{tanh}'(x)=\text{sech}^2(x)$