Bölümün türevi (bölme): formül ve çözülmüş alıştırmalar

Bu makalede iki fonksiyondan nasıl bölüm (veya bölme) elde edileceğini açıklıyoruz. Fonksiyonların bölümlerinin türevlerine ilişkin örnekler bulacaksınız ve ayrıca bölümün türevleri üzerine adım adım alıştırmalar yapabileceksiniz.

Bir bölümün türevinin formülü

Fonksiyonların bir katsayısının (veya bölümünün) türevi, pay fonksiyonunun türevi ile payda fonksiyonunun türeviyle aynıdır, pay fonksiyonundan pay fonksiyonunun türevinin yüksek payda fonksiyonunun karesine bölünmesiyle elde edilir.

bir bölümün veya bölümün türevinin formülü

Gördüğünüz gibi, bir bölümün (veya bölümün) türevine ilişkin kuralı uyguladığımızda, türevden sonra hâlâ bir kesirimiz olur. Ancak ayrıca payda iki çarpma ve bir çıkarma işlemimiz var ve payda ikinin üssüne yükseltiliyor.

Bölümlerin türevlerine örnekler

Az önce iki fonksiyonun bölümünün türevinin formülünü gördük, daha sonra bu tür işlemlerin çeşitli türev örneklerini çözeceğiz. Unutmayın, fonksiyonel bölümün nasıl türetildiğini anlamadıysanız yorum kısmından bize sorabilirsiniz.

örnek 1

Bu örnekte, bir trigonometrik fonksiyona bölünen bir potansiyel fonksiyonu türeteceğiz:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

İki farklı fonksiyonun bölümünün türevinin formülü aşağıdaki gibidir:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Bu nedenle öncelikle her fonksiyonun türevini ayrı ayrı hesaplamamız gerekir:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

Dolayısıyla tüm fonksiyonun türevi şu şekildedir:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Örnek 2

Bu durumda bir sabitin türevini bir fonksiyona bölerek bulacağız:

$f(x)=\cfrac{10}{x^2+3x-9}$

Yukarıda gördüğümüz gibi iki farklı fonksiyonun bölünmesinin türevi kuralı şu şekildedir:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Böylece pay ve paydanın türevini ayrı ayrı hesaplıyoruz:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

Ve son olarak tamsayı bölümünün türevini buluyoruz:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

Aslında payda bir sabitin bir fonksiyona bölünmesiyle doğrudan türev almak için bir formül türetebiliriz, çünkü sabitin türevi her zaman 0’dır. Bu nedenle aşağıdaki formül her zaman doğru olacaktır:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Örnek 3

Bu alıştırmada iki polinomun bir bölümünü türeteceğiz:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Türevi çözmek için, iki farklı fonksiyonun bölümünün türevi kuralını uygulamamız gerekir:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Şimdi pay polinomunun ve payda polinomunun türevini bulalım:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

Dolayısıyla polinonimlerin bölünmesinin türevi şöyledir:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

Ve son olarak işlemleri gerçekleştirip kesri mümkün olduğunca basitleştiriyoruz:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Bir bölümün türeviyle ilgili çözülmüş alıştırmalar

Aşağıdaki fonksiyon bölümlerini türetin:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Çözümü görün

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Bir bölümün türevinin gösterilmesi

Son olarak bir bölümün türevinin formülünü göstereceğiz. Bunu yapmak için türevin genel tanımını kullanacağız:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

z iki farklı fonksiyonun bir bölümü olsun:

$z(x)=\cfrac{f(x)}{g(x)}$

O zaman z fonksiyonunun matematiksel tanım uygulanarak türevi şöyle olacaktır:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

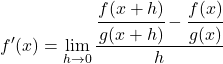
Kesirlerin payından kesirlerin çıkarılması işlemini çözüyoruz:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

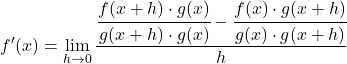
Bir denkleme toplama ve çıkarma terimi eklemek denklemi değiştirmez. Bu nedenle bir sonraki adıma geçebiliriz:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

Ortak çarpanı çıkarıyoruz:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Şimdi kesirlerin özelliklerini kullanarak h terimini paydadan paya taşıyalım:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

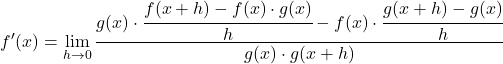
Limitlerin özelliklerini uygulayarak denklemi dönüştürüyoruz:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

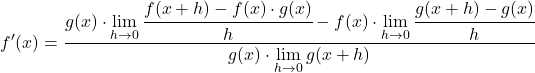
Payın sınırları her fonksiyonun türevinin matematiksel tanımına tam olarak karşılık gelir, bu nedenle:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

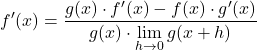
Kesrin paydasının limitini çözüyoruz:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

Ve böylece iki fonksiyonun bir bölümünün türevinin formülü gösterilmiştir:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Bir bölümün (veya bölümün) türevi

Bir bölümün türevinin formülü

Bölümlerin türevlerine örnekler

örnek 1

Örnek 2

Örnek 3

Bir bölümün türeviyle ilgili çözülmüş alıştırmalar

Bir bölümün türevinin gösterilmesi

Yorum bırakın Yanıtı iptal et