Hiperbolik sinüsün türevi

Burada hiperbolik sinüsün (formülün) nasıl türetileceğini bulacaksınız. Ek olarak hiperbolik sinüs türevinin birkaç çözülmüş örneğini göreceksiniz. Ve son olarak bu tip trigonometrik fonksiyonun türevinin formülünü kanıtlıyoruz.

Hiperbolik sinüsten türetilen formül

Hiperbolik sinüs x’in türevi, x’in hiperbolik kosinüsüdür.

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

Bu nedenle, bir fonksiyonun hiperbolik sinüsünün türevi, fonksiyonun hiperbolik kosinüsü ile o fonksiyonun türevinin çarpımına eşittir.

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Aslında yukarıdaki iki formül aynı, tek fark ikinci formülde zincir kuralını uyguluyor olmamız. Ve x’in türevi 1 olduğundan, bu fonksiyonu değiştirmez.

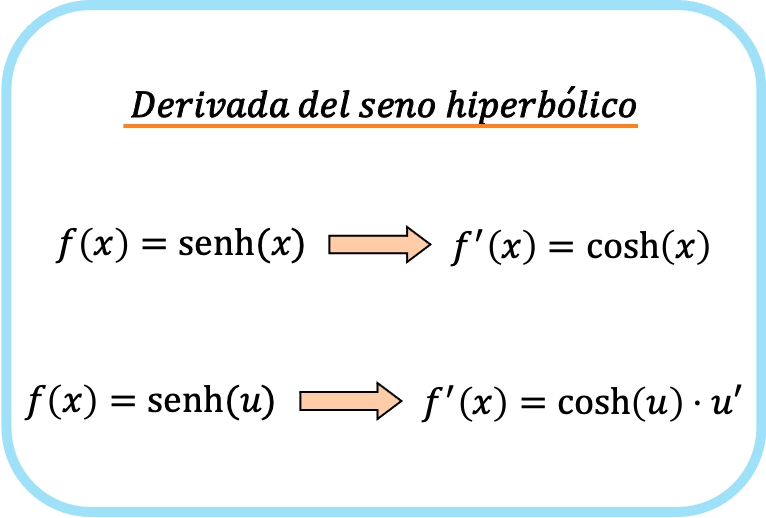
Gördüğünüz gibi hiperbolik sinüs türevinin formülü sinüs türevinin formülüne çok benzer.

Hiperbolik sinüs türevi örnekleri

Hiperbolik sinüs türevi formülünün ne olduğunu gördükten sonra, şimdi hiperbolik sinüs türevinin birkaç örneğini çözmeye devam ediyoruz. Yani bunun nasıl yapılacağı konusunda elbette hiçbir şüpheniz yok.

Örnek 1: 2x’in hiperbolik sinüsünün türevi

$f(x)=\text{senh}(2x)$

Bu durumda, hiperbolik sinüs argümanında x’ten farklı bir fonksiyonumuz var, bu nedenle türevi bulmak için hiperbolik sinüs türevi formülünü zincir kuralıyla birlikte kullanmalıyız:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

2x’in türevi 2’dir, yani 2x’in hiperbolik sinüsünün türevi, 2x çarpı 2’nin hiperbolik kosinüsü olacaktır.

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

Örnek 2: Hiperbolik sinüs x karenin türevi

$f(x)=\text{senh}(x^2)$

Hiperbolik sinüs fonksiyonunun türevinin formülü şöyledir:

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

Öte yandan ikinci dereceden x ² fonksiyonunun türevi 2x’tir. Dolayısıyla tüm fonksiyonun türevi şu şekildedir:

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$