Ark kosinüsün türevi

Burada bir fonksiyonun arkkosinüsünün nasıl elde edileceğini açıklıyoruz. Ayrıca ark kosinüs türevlerinin örneklerini bulacak ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz. Son olarak arkkosinüs türevi formülünün kanıtını size gösteriyoruz.

Ark kosinüsün türevi nedir?

X’in arkkosinüsünün türevi negatif bir bölü bir eksi x karenin kareköküdür.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

Bu nedenle, bir fonksiyonun arkkosinüsünün türevi, eksi o fonksiyonun türevinin bölümü, birin karekökü eksi o fonksiyonun karesine eşittir.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Aslında ikinci formülde x’in yerine u konularak birinci formül elde edilir. Özetlemek gerekirse, ters kosinüsün türevinin formülü şöyledir:

Gördüğünüz gibi arkkosinüsün türevinin formülü arksinüsün türevine benzer ancak ondan önce bir negatif eklenir.

Ark kosinüs türevi örnekleri

Arkosinüs fonksiyonunun türevinin formülü verildiğinde, şimdi bu tip trigonometrik türevlerin birkaç örneğini analiz edeceğiz. Bu şekilde bir fonksiyonun ark kosinüsünün nasıl türetildiğini anlamanız daha kolay olacaktır.

Örnek 1: 2x’in ark kosinüsünün türevi

$f(x)=\text{arccos}(2x)$

Ark kosinüsün türevini çözmek için formülünü kullanırız:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

2x’in türevi 2’dir, yani 2x’in ark kosinüs türevi negatif 2 bölü kök bir eksi 2x karedir:

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

Örnek 2: Ark kosinüs x karenin türevi

$f(x)=\text{arccos}(x^2)$

Türevi hesaplamak için arkkosinüs türevi formülünü zincir kuralıyla birlikte uyguluyoruz:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

x ² fonksiyonunun türevi 2x olduğundan, ark kosinüs x üzeri 2’nin türevi:

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

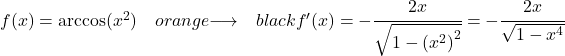
Örnek 3: Bir logaritmanın arkkosinüsünün türevi

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

Bu örnekteki fonksiyon arkkosinüs ve doğal logaritmadan oluşan bir fonksiyondur, dolayısıyla onu türetmek için zincir kuralını kullanmamız gerekir.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Doğal logaritmanın türevi bir bölü x’tir, dolayısıyla tamsayı fonksiyonunun türevi şöyledir:

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

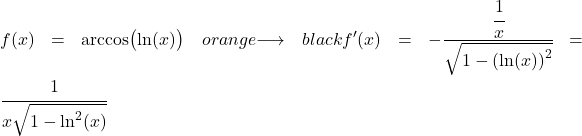
Arccosine türevi problemleri çözdü

Aşağıdaki arkkosinüs fonksiyonlarını türetin:

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

çözümü gör

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$