Dikey asimptot - Mathority

Burada bir fonksiyonun dikey asimptotlarının ne olduğunu bulacaksınız (örneklerle). Ayrıca bir fonksiyonun dikey asimptotlarının nasıl bulunacağını da açıklıyoruz ve ayrıca adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Dikey asimptot nedir?

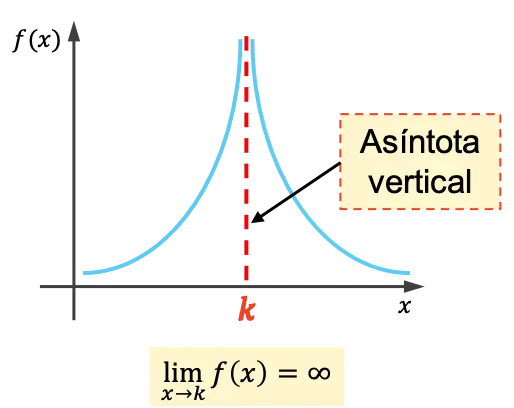
Bir fonksiyonun dikey asimptotu, grafiği onu hiç kesmeden sonsuza kadar yaklaşan dikey bir çizgidir. Bu nedenle, dikey asimptotun denklemi x=k’dir ; burada k , dikey asimptotun değeridir.

Yani, x k’ye yaklaşırken fonksiyonun limiti sonsuzsa k dikey bir asimptottur.

Bir fonksiyonun dikey asimptotu nasıl hesaplanır?

Bir fonksiyonun dikey asimptotunu hesaplamak için aşağıdaki adımlar izlenmelidir:

Fonksiyonun tanım kümesini bulun. Tüm noktalar etki alanındaysa, fonksiyonun dikey asimptotu yoktur.
Tanım kümesinde olmayan noktalarda fonksiyonun limitini hesaplayın.
Fonksiyonun dikey asimptotları, limitin sonsuzluk verdiği tüm değerler olacaktır.

Bir fonksiyonun birden fazla dikey asimptotu olabileceğini unutmayın. Örneğin, teğet fonksiyonunun grafiğinde sonsuz sayıda dikey asimptot vardır.

➤ Bakınız: teğet fonksiyonunun özellikleri

Dikey asimptot örneği

Örnek olarak, aşağıdaki rasyonel fonksiyonun tüm asimptotlarını bulacağız, böylece bunun nasıl yapıldığını görebilirsiniz:

$f(x)=\cfrac{1}{x-2}$

Genel olarak düşey asimptotların olduğu noktalar fonksiyonun tanım kümesine ait değildir. Bu nedenle öncelikle fonksiyonun tanım kümesini hesaplayacağız.

Bu rasyonel bir fonksiyon olduğundan, etki alanına ait olmayan noktaları belirlemek için paydanın kaybolduğu zamana bakarız:

$x-2=0$

$x=2$

Bu nedenle, fonksiyonun tanım kümesi x=2 dışındaki tüm gerçek sayılardır:

$\text{Dom } f = \mathbb{R} - \{2\}$

Yani x=2 fonksiyonun dikey asimptotu olabilir. Bunu doğrulamak için bu noktada fonksiyonun limitini hesaplamamız gerekir:

$\displaystyle \lim_{x \to 2} \frac{1}{x-2}=\frac{1}{2-2}=\frac{1}{0}=\infty$

Bu durumda sıfır arasında bir sayının belirsizliğini elde ettik ve bu nedenle limiti çözmek için bunun artı sonsuz mu, eksi sonsuz mu olduğunu veya limitin var olup olmadığını bilmek için yanal limitleri hesaplamamız gerekir. Ancak düşey asimptotları hesaplarken yanal limitleri yapmamıza gerek yoktur ancak bu belirsizliği elde etmek bunun düşey asimptot olduğunu söylemek için yeterlidir.

Kısaca x 2’ye yaklaşırken fonksiyonun limiti sonsuzluk verdiğinden x=2 dikey bir asimptottur.

Aşağıda grafiksel olarak gösterilen fonksiyon verilmiştir. Gördüğünüz gibi x=2 doğrusuna çok yaklaşıyor (hem soldan hem de sağdan) ama düşey bir asimptot olduğu için hiçbir zaman onunla kesişmiyor:

Ayrıca grafikten fonksiyonun x=2 noktasındaki yanal limitlerini de çıkarabiliriz:

$\displaystyle \lim_{x \to 2^-} \frac{1}{x-2} = -\infty \qquad \lim_{x \to 2^+} \frac{1}{x-2} = +\infty$

Dikey asimptot problemlerinin çözülmesi

1. Egzersiz

Aşağıdaki rasyonel fonksiyonun dikey asimptotunu hesaplayın:

$\displaystyle f(x)=\frac{3x-1}{2x-1}$

çözümü gör

Bir fonksiyonun dikey asimptotlarını hesaplamak için bir formül yoktur, ancak fonksiyonun tanım kümesini bulmanız ve fonksiyonun tanımlanmadığı noktalarda limitin sonsuzluk verdiğini görmeniz gerekir.

Bu nedenle, tanım kümesine ait olmayan noktaları bulmak için rasyonel fonksiyonun paydasını 0’a eşitliyoruz:

$2x -1 =0$

$2x= 1$

$x = \cfrac{1}{2}$

Dolayısıyla fonksiyonun tanım kümesi x=1/2 dışındaki tüm gerçek sayılardır:

$\text{Dom } f = \mathbb{R} - \left\{ \cfrac{1}{2} \right\}$

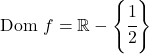
Yani x=1/2 dikey bir asimptot olabilir. Bunu kontrol etmek için bu noktada fonksiyonun limitini hesaplıyoruz:

$\displaystyle \lim_{x \to \frac{1}{2} } \cfrac{3x-1}{2x-1} = \cfrac{3\cdot\cfrac{1}{2}-1}{2\cdot\cfrac{1}{2}-1} = \cfrac{ \cfrac{3}{2} -1 }{\cfrac{2}{2} -1 } = \cfrac{ \cfrac{1}{2} }{1-1}=\cfrac{\cfrac{1}{2}}{0} =\infty$

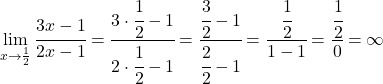
Fonksiyonun bu noktadaki limiti sonsuzluğu verdiği için x=1/2 dikey bir asimptottur .

Alıştırma 2

Aşağıdaki kesirli fonksiyonun tüm dikey asimptotlarını bulun:

$\displaystyle f(x)=\frac{2x+1}{x^2-9}$

çözümü gör

İlk olarak, hangi değerlerin fonksiyonun tanım kümesinde olmadığını görmek için kesrin paydasını sıfıra eşitliyoruz:

$x^2-9=0$

Tamamlanmamış ikinci dereceden denklemi çözüyoruz:

$x^2=9$

$x=\pm 3$

Dolayısıyla rasyonel fonksiyonun alanı şu şekildedir:

$\text{Dom } f = \mathbb{R} - \left\{3, -3\right\}$

Dolayısıyla, bu iki değerden hangisinin dikey asimptot olduğunu belirlemek için fonksiyonun her noktadaki limitini çözüyoruz:

$\displaystyle\lim_{x \to 3}\frac{2x+1}{x^2-9}=\frac{2\cdot3+1}{3^2-9}=\frac{7}{9-9}=\frac{7}{0}=\infty$

$\displaystyle\lim_{x \to -3}\frac{2x+1}{x^2-9}=\frac{2\cdot(-3)+1}{(-3)^2-9}=\frac{-5}{9-9}=\frac{-5}{0}=\infty$

İki limit sonsuzluğu verir, dolayısıyla x=3 ve x=-3 problem fonksiyonunun iki dikey asimptotudur .

Alıştırma 3

Eğer varsa, aşağıdaki rasyonel fonksiyonun tüm dikey asimptotlarını bulun:

$\displaystyle f(x)=\frac{x+3}{x^2+2x-3}$

➤ Bakınız: sıfır belirsizlik arasında sıfır

çözümü gör

Öncelikle kesrin paydasını sıfırlayan değerleri bulmak için ikinci dereceden payda denklemini çözüyoruz:

$x^2+2x-3=0$

$\begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}$

Yani fonksiyonun etki alanı:

$\text{Dom } f = \mathbb{R} - \left\{1, -3\right\}$

Dolayısıyla ilk önce fonksiyonun x=1 noktasındaki limitini hesaplıyoruz:

$\displaystyle\lim_{x \to 1}\frac{x+3}{x^2+2x-3}=\frac{1+3}{1^2+2\cdot 1-3}=\frac{4}{0}=\infty$

Diğer taraftan fonksiyonun limitini x -3’e doğru gittiğinde çözüyoruz:

$\begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}$

Önceki limit, sıfır arasında sıfır belirsiz formunu verir, dolayısıyla bunu çözmek için polinomları çarpanlara ayırmamız gerekir. Limiti nasıl çözdüğümüze dair herhangi bir şüpheniz varsa, bu tür belirsizliğin nasıl çözüleceğine ilişkin tam açıklamayı alıştırma cümlesi bağlantısında görebilirsiniz.

Bu durumda, fonksiyonun yalnızca x=1 noktasındaki limiti sonsuzluğu verir, dolayısıyla x=1, fonksiyonun tek dikey asimptotudur .

Dikey asimptot nedir?

Bir fonksiyonun dikey asimptotu nasıl hesaplanır?

Dikey asimptot örneği

Dikey asimptot problemlerinin çözülmesi

1. Egzersiz

Alıştırma 2

Alıştırma 3

Yorum bırakın Yanıtı iptal et