Sonsuz (∞/∞) arasındaki sonsuz belirsizlik

Bu yazıda sonsuz (∞/∞) arasındaki belirsizliğin sonsuzluğunun nasıl hesaplanacağını açıklıyoruz. Bu belirsizliğin örneklerini her türlü fonksiyonda bulacaksınız: polinom, radikal, üstel fonksiyonlar, vb. Ayrıca sonsuzluklar arasında sonsuz belirsizlikler veren limitlerin adım adım çözüldüğü egzersizlerle antrenman yapabileceksiniz.

Sonsuz arasındaki sonsuz belirsizlik nasıl çözülür?

Bir fonksiyonun limiti sonsuz bölü sonsuz değerini veriyorsa, bu onun bir belirsizlik (veya belirsiz form) olduğu anlamına gelir. Sonsuzlar arasındaki belirsizliğin sonsuzluğunu veren bir fonksiyonun limitini çözmek için pay polinomunun derecesinin payda polinomunun derecesi ile karşılaştırılması gerekir.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

Belirsizlik sonsuzluğunun sonsuza bölünmesinin sonucu, kesrin payının derecesine ve paydasının derecesine bağlıdır:

Pay polinomunun derecesi payda polinomunun derecesinden küçükse, belirsizliğin sonsuzluğunun sonsuza bölümü sıfıra eşittir.
Pay polinomunun derecesi payda polinomunun derecesine eşdeğerse, sonsuz üzerindeki sonsuz belirsizlik , iki polinomun baş katsayılarının bölümüdür.
Pay polinomunun derecesi payda polinomunun derecesinden büyükse, sonsuzluk arasındaki belirsizliğin sonsuzluğu az ya da çok sonsuzluk verir (işaret, iki polinomun ana terimlerine bağlıdır).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ Sonsuzluk arasındaki sonsuz belirsizlik örnekleri

Her durumun birkaç örneğine bakarak, sonsuzluk arasındaki belirsiz form sonsuzluğunun nasıl çözüldüğünü görelim:

payın derecesi paydanın derecesinden küçük

Yukarıda gördüğümüz gibi pay polinomunun derecesi payda polinomunun derecesinden küçük olduğunda sonsuzlar arasındaki sonsuz belirsiz limit her zaman 0 verir.

Örnek 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Payın polinomu ikinci dereceden, paydanın polinomu üçüncü dereceden olduğundan limitin çözümü 0’dır.

Örnek 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

Payın polinom fonksiyonu birinci derecedendir, ancak paydanın fonksiyonu dördüncü derecedendir, dolayısıyla negatif sonsuzluğun limiti 0’dır.

payın derecesi paydanın derecesine eşit

Pay polinomunun derecesi payda polinomunun derecesine eşit olduğunda, sonsuzluğun belirsiz limiti, iki polinomun baş katsayılarının (yüksek dereceli terimin katsayısı) bölünmesiyle hesaplanır.

Örnek 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Bu durumda iki polinom ikinci derecedendir, dolayısıyla pozitif sonsuzdaki limiti bulmak için yüksek dereceli terimlerin katsayılarını bölmek gerekir.

Örnek 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

Limit, x’in eksi sonsuza doğru yöneldiği zaman olmasına rağmen, sonsuzluk arasındaki sonsuz belirsizlik aynı şekilde çözümlenir.

Payın derecesi paydanın derecesinden büyük

Pay polinomunun derecesi payda polinomunun derecesinden büyük olduğunda, sonsuzluk arasındaki belirsiz sonsuz biçimi her zaman sonsuzluğu verecektir ve sonsuzluğun işareti iki polinomun yüksek dereceli terimleri tarafından belirlenir.

Örnek 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Payın fonksiyonu paydanınkinden daha yüksek bir dereceye sahiptir, dolayısıyla sonsuz üzerindeki belirsizlik sonsuzluğu verir. Ayrıca bu durumda hem pay hem de payda pozitif sonsuzluk aldığından limitin sonucunun da pozitif olması gerekir.

Örnek 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Bu problemde karesi pozitif olan herhangi bir terim pozitif olduğundan paydan pozitif bir sonsuzluk elde edilirken, paydadan negatif bir sonsuzluk elde edilir. Bu nedenle, ortaya çıkan sınır negatiftir çünkü pozitifin negatife bölümü negatife eşittir.

Köklü sonsuzluk arasında sonsuz belirsizlik

Az önce polinom fonksiyonlarımız olduğunda sonsuzluk arasındaki sonsuz belirsizliği nasıl hesaplayacağımızı gördük. Ama… eğer köklerimiz varsa, sonsuzluğun sonsuza bölümü ne kadardır?

İrrasyonel bir fonksiyonun derecesi (köklü fonksiyon), ana terimin derecesi ile radikalin indeksi arasındaki bölümdür.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Dolayısıyla köklü bir fonksiyonun limiti sonsuzluk arasındaki belirsizliği veriyorsa , yukarıda açıklanan kuralları pay ve paydanın dereceleri için uygulamalıyız, ancak kökleri olan bir polinomun derecesinin farklı hesaplandığını dikkate almalıyız.

Köklü bir fonksiyonun sonsuzluğa sınırına ilişkin aşağıdaki örneğe bakın:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Payın derecesi 2, paydanın derecesi 4 (8/2=4) olduğundan payın derecesi paydanın derecesinden küçük olduğundan limit 0’dır.

Öte yandan pay ve paydanın derecesi eşitse belirsiz sınırı hesaplamak için radikalle birlikte ana katsayıyı almamız gerekir:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

Üstel fonksiyonlarla sonsuz arasında sonsuz belirsizlik

Son olarak, yalnızca sonsuzlukların belirsizlik bölümü durumunu incelememiz gerekiyor: Sonsuzluk ve üstel fonksiyonlar arasındaki sonsuz belirsizlik ne kadardır?

Üstel bir fonksiyonun büyümesi, bir polinom fonksiyonunun büyümesinden çok daha büyüktür, bu nedenle üstel bir fonksiyonun derecesinin, bir polinom fonksiyonunun derecesinden daha büyük olduğunu dikkate almalıyız.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Bu nedenle, sonsuz belirsizliğin sonsuzluğa bölümü üstel fonksiyonlara sahip bir limitten kaynaklanıyorsa, pay ve paydanın dereceleri için açıklanan kuralların aynısını uygulamak yeterlidir, ancak üstel bir fonksiyonun polinomdan daha yüksek mertebede olduğu dikkate alınır. . Ek olarak, bölümün pay ve paydasında üstel fonksiyonlarımız varsa, tabanı daha büyük olan üstel fonksiyon daha yüksek mertebeden olacaktır. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

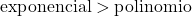
Bu durumda payda üstel bir fonksiyondan oluştuğu için paydan daha yüksek mertebededir. Dolayısıyla sonsuzluk arasındaki belirsiz form sonsuzluğu ortadan kalkar.

Sonsuzluk arasındaki sonsuz belirsizlikle ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki rasyonel fonksiyonun limitini hesaplayın:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

Çözüme bakın

Limiti hesaplarken sonsuzluk arasındaki sonsuz belirsizliği elde ederiz ancak payın derecesi paydanın derecesinden küçük olduğundan belirsizlik limiti sıfıra eşittir.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

Alıştırma 2

Aşağıdaki belirsiz limiti çözün:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

Çözüme bakın

Limiti hesaplamaya çalışırken belirsizlik ∞/∞ elde edilir. Bu durumda pay polinomunun derecesi payda polinomunun derecesinden büyük olduğundan belirsiz limit artı sonsuza eşittir.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

Alıştırma 3

Aşağıdaki limiti sonsuzda çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Çözüme bakın

Limit, artı sonsuz arasındaki belirsizliği eksi sonsuzluğu verir. Payın derecesi paydanın derecesinden büyüktür, dolayısıyla belirsiz limit artı sonsuza eşittir. Ancak negatif sonsuzun pozitif sonsuza bölümü olduğundan sonuç eksi sonsuzdur.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Alıştırma 4

Aşağıdaki belirsiz limiti çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Çözüme bakın

Bu problemde, sonsuz belirsiz form/sonsuzluk aynı dereceden iki polinomun bölümünden elde edilir, dolayısıyla belirsiz limitin sonucu bunların ana katsayılarının bölümüdür:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Alıştırma 5

Aşağıdaki limiti en az sonsuza kadar hesaplayın:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Çözüme bakın

Payın cebirsel ifadesinin derecesi paydanın ifadesinin derecesinden küçüktür, dolayısıyla +∞/+∞ belirsizliği 0 verir:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Alıştırma 6

Kökleri olan bir fonksiyonun aşağıdaki belirsiz limitini çözün:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Çözüme bakın

Payın ifadesi bir radikalin altındadır, dolayısıyla derecesi 7/3’tür. Öte yandan paydadaki polinom ikinci derecedendir. Ve 7/3>2 olduğundan limit artı sonsuzluğu verir:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

Egzersiz 7

Aşağıdaki fonksiyonun sonsuzluğa olan sınırını kesirlerle belirleyin:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Çözüme bakın

Bu alıştırmada, belirsizlik eksi sonsuz bölü eksi sonsuz, payın derecesinin paydanın derecesinden büyük olmasıyla elde edilir, dolayısıyla:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Egzersiz 8

Aşağıdaki fonksiyonun en azından sonsuza kadar olan limitini bulun:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Çözüme bakın

Payda polinomu ikinci dereceden, pay polinomu ise doğrusaldır. Dolayısıyla belirsizliğin sonsuzunun sonsuza bölümü 0 verir.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Egzersiz 9

Aşağıdaki fonksiyonun en az sonsuz limitini çözün:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Çözüme bakın

Pay, paydadan daha büyük olduğundan, ∞/∞ belirsiz formunun sonucu sonsuz olacaktır. Ek olarak, sonsuzluk işareti negatif olacaktır çünkü pozitifin negatife bölümü negatifi verir:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Egzersiz 10

Sonsuzluk arasındaki sonsuz belirsizlikle aşağıdaki limiti çözün:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Çözüme bakın

Üstel fonksiyon polinom fonksiyonundan daha yüksek mertebede olduğundan limit sonsuzluğu verecektir. Ancak pozitifi negatife böldüğümüzde sonsuzluk işareti negatif olacaktır:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Egzersiz 11

Aşağıdaki limiti hesaplayın:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

Çözüme bakın

Bu problemde, sonsuz üzerinde sonsuz belirsizliği, aynı dereceden oldukları için iki polinomun baskın katsayılarının bölünmesiyle çözülür:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

Egzersiz 12

x sonsuza yaklaşırken aşağıdaki fonksiyonun limitini çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

Çözüme bakın

Paydaki bilinmeyenin doğrudan karesi alınmamasına rağmen, dikkate değer özdeşlik çözümünde payın derecesinin paydanın derecesinden büyük olduğunu açıkça görebiliriz. Henüz:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Egzersiz 13

Aşağıdaki fonksiyonun sonsuzluğa olan sınırını küp kök kullanarak hesaplayın:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

Çözüme bakın

Pay küp kökten oluştuğu için derecesi 3/3=1’dir. O halde payın derecesi paydanın derecesine eşit olduğundan sonsuzluk arasındaki sonsuz belirsizlik şu şekilde çözülür:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

Egzersiz 14

Aşağıdaki fonksiyonun sonsuza limitini iki radikalle çözün:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Çözüme bakın

Payın derecesi 7/3 = 2,33 ve paydanın derecesi 5/2 = 2,5’tir. Dolayısıyla payın derecesi paydanın derecesinden küçük olduğundan sonsuz arasındaki belirsiz sonsuz sınır 0’dır:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Egzersiz 15

Aşağıdaki limiti hesaplayın:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Çözüme bakın

Payın derecesi ne olursa olsun, paydada üstel bir fonksiyona sahip olduğumuz için sonsuz/sonsuz belirsiz formunun sonucu 0 olur:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$