Polinom fonksiyonu

Burada polinom fonksiyonlarının ne olduğunu ve tüm polinom fonksiyon türlerinin ne olduğunu bulacaksınız. Ayrıca polinom fonksiyonlarının özelliklerini de açıklıyoruz.

Polinom fonksiyonu nedir?

Bir polinom fonksiyonu, cebirsel ifadesi bir polinom olan bir fonksiyondur , yani bir polinom fonksiyonu, farklı derecelerdeki sonlu sayıda terimin toplanması veya çıkarılmasıyla tanımlanır.

Bu nedenle, bir polinom fonksiyonu matematiksel olarak aşağıdaki ifadeyle tanımlanır:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Öte yandan polinom fonksiyonları aşağıdaki formül kullanılarak da tanımlanabilir:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

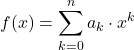
şartlar nerede

$a_k$

$x^k$

polinom fonksiyonunu oluşturan her monomiyalin sırasıyla katsayısı ve değişkenidir.

Dönem

$a_nx^n$

Ana terim olarak adlandırılan , fonksiyonun en yüksek dereceli monomiyal olması nedeniyle polinom fonksiyonunun derecesini gösterir. Başka bir deyişle en büyük değer üssü polinom fonksiyonunun derecesini gösteren üssüdür.

Aşağıda polinom fonksiyonlarının daha fazla özelliğini görecek olsak da, herhangi bir polinom fonksiyonunun tanım kümesinin tamamı gerçek sayılardır.

Polinom fonksiyon türleri

Polinom fonksiyonunun tanımı verildiğinde, şimdi tüm polinom fonksiyon türlerinin mevcut olduğunu göreceğiz.

sabit fonksiyon

Sabit fonksiyon, derecesi 0 olan bir polinom fonksiyonudur, yani bağımsız değişkenin (x) herhangi bir değeri için her zaman aynı görüntüyü alan bir fonksiyon türüdür.

Sabit fonksiyonun genel ifadesi aşağıdaki gibidir:

$f(x)=k$

Örneğin, aşağıdaki üç fonksiyon sıfır dereceli sabitler veya polinom fonksiyonlardır:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

Sabit bir fonksiyonun grafiksel gösterimi, değeri sabite eşit olan yatay bir çizgidir (x eksenine paralel).

Bu tür işlevlerle ilgili daha fazla özelliği aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: sabit fonksiyonun özellikleri

Doğrusal fonksiyon

Afin fonksiyon olarak da adlandırılan doğrusal fonksiyon , birinci dereceden bir polinom fonksiyonudur. Dolayısıyla bu tür bir polinom fonksiyonu yalnızca bir doğrusal terim ve bağımsız bir terimden oluşabilir:

$f(x)=mx+n$

Altın

$m$

çizginin eğimi ve

$n$

y-kesme noktasıdır, yani fonksiyonun Y eksenini kestiği yerdir.

Doğrusal fonksiyonlara veya birinci dereceden polinom fonksiyonlarına örnekler:

$f(x)=4x+3\qquad f(x)=-5x$

Bazıları, fonksiyonun terimi olup olmadığına bağlı olarak doğrusal fonksiyonu afin fonksiyondan ayırır.

$n$

ya da değil, kesme noktası olan afin fonksiyon ve olmayan doğrusal fonksiyon.

Doğrusal fonksiyonların grafiksel gösterimi her zaman eğim derecesi fonksiyonun eğim değerine bağlı olan çizgilerdir.

Aşağıda birinci derece polinom fonksiyonunu grafiksel olarak görebilirsiniz.

$f(x)=2x-1.$

Ancak doğrusal bir fonksiyonun grafiğini çizmek için çeşitli kavramlar hakkında net olmanız gerekir. Aşağıdaki bağlantıda bu tür bir polinom fonksiyonunun grafiğinin nasıl çizileceğinin adım adım açıklamasını bulacaksınız:

➤ Bakınız: Doğrusal bir fonksiyonun grafiksel gösterimi

İkinci dereceden fonksiyon

İkinci dereceden bir fonksiyon, 2. dereceden bir polinom fonksiyonudur, yani yüksek dereceli terimi ikinci dereceden olan bir fonksiyondur.

Bu nedenle ikinci dereceden bir fonksiyonun formülü şöyledir:

$f(x)=ax^2+bx+c$

Altın

$ax^2$

ikinci dereceden terimdir,

$bx$

doğrusal terim ve

$c$

polinom fonksiyonunun bağımsız terimi.

İkinci dereceden fonksiyonlara veya ikinci dereceden polinom fonksiyonlara örnekler:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

İkinci dereceden bir fonksiyonun grafiği her zaman bir paraboldür ve şekli baş katsayının işaretine bağlıdır.

$a:$

Eğer katsayı
$a$

pozitifse ikinci dereceden fonksiyon dışbükeydir (şeklindedir)

$\bm{\cup}$

).
Bunun yerine, eğer katsayı
$a$

negatifse, ikinci dereceden fonksiyon içbükeydir (şeklindedir)

$\bm{\cap}$

).

Dolayısıyla, ikinci dereceden polinom fonksiyonunun ana katsayısının işaretiyle grafiğinin alacağı şekli bilebiliriz, ancak tam grafiksel gösterimini yapmak için özel bir prosedür izlenmelidir. Bu prosedürü aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: İkinci dereceden bir fonksiyonun grafiksel gösterimi

kübik fonksiyon

Kübik fonksiyon üçüncü dereceden bir polinom fonksiyonudur. Dolayısıyla bu tür polinom fonksiyonları cebirsel olarak şu şekilde ifade edilir:

$f(x)=ax^3+bx^2+cx+d$

Kübik fonksiyonlara veya üçüncü derece polinom fonksiyonlarına örnekler:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

Kübik fonksiyonların grafiksel gösterimleri kübik eğrilere karşılık gelir. Ancak bu tür fonksiyonları bir grafikte temsil etmek için karmaşık bir prosedürün izlenmesi gerekir (türevleri de içerir). Burada nasıl yapıldığını görebilirsiniz:

➤ Bakınız: Bir fonksiyon nasıl temsil edilir

Gördüğünüz gibi, bir polinom sonsuz terime sahip olabileceğinden, polinom fonksiyonlarının türleri aslında sonsuzdur. Yani, örneğin, dördüncü dereceden bir fonksiyon kübik fonksiyona benzer, ancak ikinci dereceden bir terimin eklenmesiyle oluşur. Önemli olan polinom fonksiyonunun türünün, fonksiyonun derecesi tarafından belirlendiğini anlamanızdır.

Polinom fonksiyonların özellikleri

Polinom fonksiyonları aşağıdaki özelliklere sahiptir:

Herhangi bir polinom fonksiyonunun tanım kümesi gerçek sayılar kümesidir.

$\text{Dom } f=\mathbbf{R}$

Tüm polinom fonksiyonları süreklidir.

Derecesi 1’den büyük olan polinom fonksiyonlarının asimptotu yoktur.

Polinom fonksiyonunun türü ne olursa olsun, ordinat ekseni (Y ekseni) ile tek kesişme noktası bağımsız teriminin yüksekliğinde, yani aşağıdaki noktadadır:

$(0,a_0)$

Öte yandan, bir polinom fonksiyonu apsis eksenini (X ekseni) en fazla fonksiyonun derecesi kadar keser.

Bir polinom fonksiyonunun yalnızca çift dereceli terimleri varsa, bu onun OY eksenine göre simetrik olduğu anlamına gelir. Öte yandan, eğer bir polinom fonksiyonunun yalnızca tek dereceli terimleri varsa, bu, fonksiyonun koordinatların orijinine göre simetrik olduğu anlamına gelir.

Bir polinom fonksiyonunun göreceli ekstrema sayısı (maksimum veya minimum), en fazla, fonksiyonun polinomunun derecesi eksi 1’dir.

Bir polinom fonksiyonunun dönüm noktalarının sayısı en fazla fonksiyonun polinomunun derecesi eksi 2’ye eşittir.

İşlemler polinom fonksiyonlarıyla gerçekleştirilebilir:
- İki polinom fonksiyonunun toplamı başka bir polinom fonksiyonunu verir.
- İki polinom fonksiyonunun çarpımı başka bir polinom fonksiyonunu doğurur.
- Bir polinom fonksiyonunun bir skalerle (gerçek sayı) çarpılması benzer bir polinom fonksiyonuyla sonuçlanır, ancak grafiği küçültülmüş veya genişletilmiştir.
- İki polinom fonksiyonunun bileşimi başka bir polinom fonksiyonuna eşittir.