Doğrudan orantı fonksiyonu

Bu yazımızda doğru orantı fonksiyonlarının ne olduğunu, formüllerinin ne olduğunu, grafikte nasıl gösterileceğini ve belirli bir noktadan denklemlerinin nasıl hesaplanacağını açıklıyoruz.

Doğru orantılılık fonksiyonu nedir?

Doğru orantı fonksiyonu, iki doğrudan orantılı büyüklüğü ilişkilendiren bir fonksiyondur. Bu nedenle bağımlı değişkenin (y) değerini hesaplamak için bağımlı değişkenin (x) değerinin orantı sabiti ile çarpılması gerekir.

Doğru orantı fonksiyonuna doğrusal fonksiyon da denir.

Bir niceliğin değeri artarken diğerinin değeri artıyorsa (veya tam tersi) iki niceliğin doğru orantılı olduğunu unutmayın.

Doğru orantı fonksiyonu formülü

Doğru orantı fonksiyonunu tanımlayan formül aşağıdaki gibidir:

$y=mx$

burada y bağımsız değişkendir, x bağımlı değişkendir ve ym fonksiyonun eğimi veya orantı sabitidir.

Gördüğünüz gibi, bu formülle y büyüklüğünün değerlerini hesaplamak çok kolaydır, sadece x büyüklüğünün değerini her bir doğru orantı fonksiyonunun özelliği olan fonksiyonun eğimi ile çarpmanız yeterlidir.

Örneğin, aşağıdaki doğrudan orantı fonksiyonuna sahipsek:

$y=3x$

X 5 olduğunda y miktarının ne kadar olduğunu belirlemek istiyorsak, fonksiyonun (3) eğimini 5 ile çarpmamız yeterlidir:

$y=3\cdot 5=15$

Doğrudan orantı fonksiyonunun grafiksel gösterimi

Daha sonra doğru orantı fonksiyonlarının grafiğinin nasıl çizileceğini göreceğiz. Örnek olarak aşağıdaki alıştırmayı yapacağız:

$y=2x$

Doğrudan orantı fonksiyonunu bir grafik üzerinde temsil etmek için, koordinatların orijininden ((0,0)) geçen ve fonksiyonun eğimine sahip bir çizgi çizmeniz yeterlidir.

Bu durumda temsil etmek istediğimiz fonksiyonun eğimi

$m=2$

Bu nedenle doğrunun her x birimi için iki birim y kadar büyümesi gerekir.

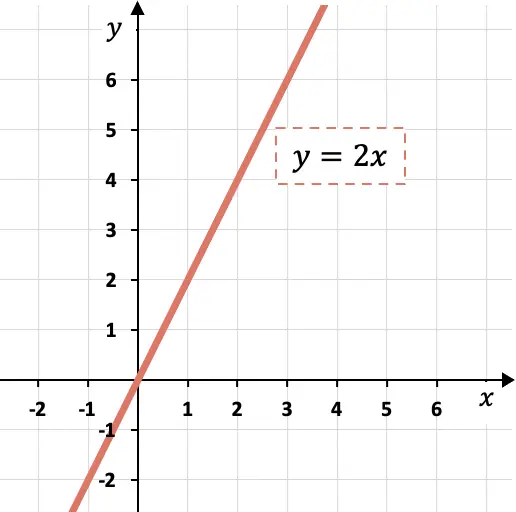
Grafikten de görebileceğiniz gibi eğim 2’ye eşitse bu, y büyüklüğünün x büyüklüğünün iki katı kadar arttığı anlamına gelir.

Doğru orantılılık fonksiyonları, afin fonksiyonlara çok benzer bir grafiğe sahiptir, ancak bunlar iki farklı fonksiyon türüdür. Aşağıdaki bağlantıda afin fonksiyon ile doğrusal fonksiyon arasındaki farkların ne olduğunu görebilirsiniz:

➤ Bakınız: doğrusal ve afin fonksiyon arasındaki fark

Doğru orantılılık fonksiyonu nasıl bulunur?

Doğru orantı fonksiyonunun bir noktasını biliyorsak denklemini kolaylıkla bulabiliriz. Doğrudan orantı fonksiyonu problemini çözerek bunun nasıl yapıldığını görelim:

Bir ressamın boyadığı oda sayısı, çalıştığı saatle yaklaşık olarak doğru orantılıdır, yani ne kadar çok çalışırsa o kadar çok odayı boyayabilir. Eğer 8 saatlik bir günde iki odanın tamamını boyadığını biliyorsak, boyanan oda sayısını çalışılan saatlerle ilişkilendiren doğru orantı fonksiyonu nedir?

Öncelikle hangisinin bağımlı, hangisinin bağımsız olduğunu belirlememiz gerekiyor. Boyanan parçaların sayısı çalışılan saatlere bağlıdır, tersi geçerli değildir. Dolayısıyla bağımsız değişken (x) çalışılan saat sayısı, bağımlı değişken (y) ise boyanan oda sayısıdır.

Problem bize ressamın 2 odayı 8 saatte boyayabileceğini, dolayısıyla fonksiyonun grafiğinin (8,2) noktasından geçmesi gerektiğini söylüyor.

$(8,2)$

Ek olarak bu ifade, iki niceliğin doğru orantılı bir ilişkiye sahip olduğunu, yani bunların matematiksel olarak doğrudan orantı fonksiyonu formülüyle ilişkili olduğunu belirtir:

$y=mx$

Artık fonksiyonun eğiminin değerini, (8,2) noktasının koordinatlarını denklemde değiştirerek hesaplayabiliriz:

$y=mx \ \xrightarrow{x=8 \ ; \ y=2}\ 2=m\cdot 8$