Bu makalede simetrik fonksiyonların ne olduğunu (çift ve tek fonksiyonlar) ve bir fonksiyonun simetrisinin nasıl çalışılacağını açıklıyoruz. Ayrıca bu tip fonksiyonların özelliklerini de görebileceksiniz ve son olarak simetrik fonksiyonlarla ilgili adım adım çözülen alıştırmalarla pratik yapabileceksiniz.
Simetrik fonksiyon nedir?
Simetrik bir fonksiyon, grafiksel gösteriminde bir simetri ekseninin bulunabildiği bir fonksiyondur. İki tür simetrik fonksiyon vardır: Y eksenine göre simetrik olan çift fonksiyonlar ve koordinatların orijinine göre simetrik olan tek fonksiyonlar.
Simetri ekseninin, herhangi bir şeyi zıt noktaları birbirine eşit uzaklıkta olacak şekilde iki parçaya bölen hayali bir çizgi olduğunu unutmayın.
eşit işlevler
Çift fonksiyonlar , y eksenine göre simetrik olan fonksiyonlardır; yani Y ekseni, fonksiyonun simetri eksenidir.
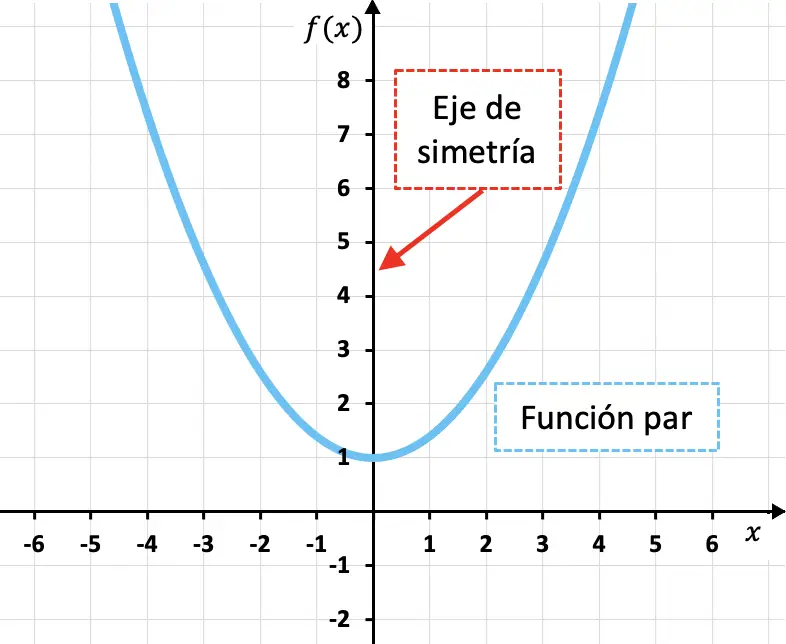
Yukarıda gösterilen ikinci dereceden fonksiyonda görebileceğiniz gibi, bağımsız değişkenin (x) herhangi bir değeri için çift fonksiyonun görüntüsü, fonksiyonun karşıt değeri (-x) için görüntüsüne eşdeğerdir. Başka bir deyişle, matematiksel olarak bir fonksiyon aşağıdaki koşulu karşılasa bile fonksiyondur:
![]()
Çift fonksiyonlar bir tür simetrik fonksiyondur, şimdi tek fonksiyonların neye benzediğine bakalım.
tek işlevler
Tek fonksiyonlar koordinatların orijinine göre yani (0,0) noktasına göre simetrik olan fonksiyonlardır.
Aşağıda garip bir fonksiyonun grafiğini görebilirsiniz:
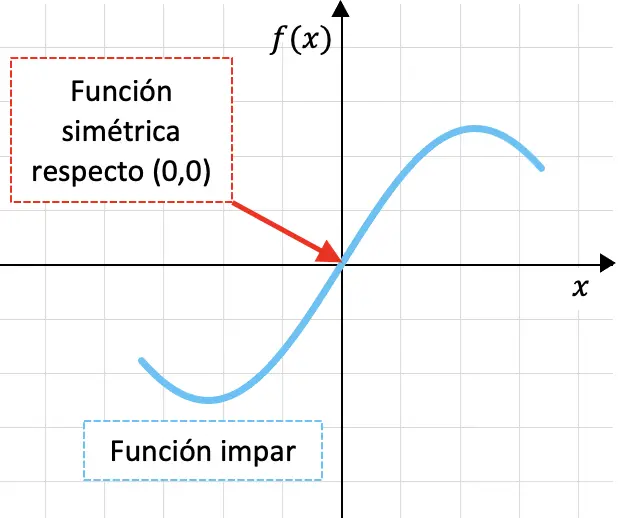
Bir fonksiyonun koordinat orijinine göre simetrik olması, fonksiyonun grafiğini önce OY ekseninden, sonra OX ekseninden katlarsak fonksiyonun grafiğinin örtüşeceği anlamına gelir.
Cebirsel olarak, bir fonksiyon, görüntüleri arasında aşağıdaki ilişki sağlanıyorsa tektir:
![]()
Bir fonksiyonun simetrisini bilmek, onu temsil etmede çok faydalıdır çünkü grafiğin yalnızca yarısını bildiğimizde diğer kısmını hızlıca çizebiliriz.
Bir fonksiyonun simetrisi nasıl bulunur?
Bir fonksiyonun simetrisini incelemek için görüntüsünü hesaplamamız gerekir.
![]()
yani hesaplamak gerekiyor
![]()
Yani görüntünün sonucuna bağlı olarak fonksiyonun simetrisi şöyle olacaktır:
- eğer doldurulursa
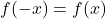
fonksiyon eşit ve dolayısıyla Y eksenine göre simetriktir.
- eğer doldurulursa
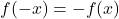
fonksiyon tektir ve bu nedenle koordinatların orijinine göre simetriktir.
- Yukarıdaki koşullardan hiçbiri karşılanmıyorsa, bu asimetrik bir fonksiyondur (simetri ekseni yoktur).
Örneğin aşağıdaki kübik fonksiyonun simetrisini analiz edelim:
![]()
Fonksiyonun simetrisini incelemek için şunu hesaplıyoruz:
![]()
![]()
Ortaya çıkan cebirsel ifade, orijinal fonksiyon ifadesine eşdeğerdir ancak işareti değişmiştir veya başka bir deyişle aşağıdaki eşitlik sağlanır:
![]()
Bu nedenle fonksiyon tektir ve dolayısıyla koordinatların (0,0) orijinine göre simetriktir.
Simetrik fonksiyonların özellikleri
Simetrik fonksiyonlar aşağıdaki özelliklere sahiptir:
- İki çift/tek fonksiyonun toplamı başka bir çift/tek fonksiyona eşittir.
- İki çift fonksiyonun veya iki tek fonksiyonun çarpımı bir çift fonksiyon verir.
- Bir çift/tek fonksiyonunun türevi bir çift/tek fonksiyondur.
- İki çift/tek fonksiyon arasındaki bileşim, bir çift/tek fonksiyona eşdeğerdir.
- Hem çift hem de tek olan, yani OY eksenine ve orijine göre simetrik olan tek fonksiyon, fonksiyondur.
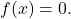
Bir fonksiyonun simetrisiyle ilgili çözülmüş problemler
1. Egzersiz
Aşağıdaki fonksiyonun simetrisini bulun:
![]()
Fonksiyonun simetrisini hesaplamak için şunu değerlendirmemiz gerekir:
![]()
![]()
Üslü bir negatif sayının herhangi bir kuvveti pozitif bir sayı verir; dolayısıyla bu durumda aşağıdaki denklem doğrudur:
![]()
Bu nedenle fonksiyon çifttir ve dolayısıyla y eksenine (Y ekseni) göre simetriktir.
Alıştırma 2
Aşağıdaki rasyonel fonksiyonun simetrisini inceleyin:
![]()
Fonksiyonun simetrisini belirlemek için şunu yaparız:
![]()
![]()
Bu problemde herhangi bir simetri koşulu sağlanmamaktadır çünkü görüntü
![]()
eşit değildir
![]()
ne de
![]()
![]()
Bu nedenle fonksiyonun bir simetri ekseni yoktur, daha ziyade asimetrik bir fonksiyondur.
Alıştırma 3
Aşağıdaki fonksiyonun simetrisini hesaplayın:
![]()
Fonksiyonun simetrisini analiz etmek için şunu hesaplamamız gerekir:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(-x)&=2(-x)|(-x)|\\[2ex]&=-2x|-x|\\[2ex]&=-2x|x|\\[2ex]&=-(2x|x|)\\[2ex]&=-f(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d939238f353c0ab70492a66466dd0569_l3.png)
Bu durumda, ortaya çıkan ifade orijinal ifadeye benzer ancak işaret değişikliği ile aşağıdaki denklem yerine getirilir:
![]()
Bu nedenle fonksiyon tektir ve dolayısıyla koordinatların (0,0) orijinine göre simetriktir.