Weierstrass teoremi

Bu yazıda Weierstrass teoreminin tanımını bulacaksınız. Ayrıca Weierstrass teoremini mükemmel bir şekilde anlamak için adım adım çözülen çeşitli alıştırmalarla pratik yapabileceksiniz.

Weierstrass teoreminin ifadesi

Weierstrass teoremi, eğer bir fonksiyon kapalı bir aralıkta sürekli ise, o fonksiyonun o aralıkta bir mutlak maksimuma ve bir mutlak minimuma sahip olduğunu söyler.

➤ Bakınız: Sürekli fonksiyon nedir?

Weierstrass teoremi sadece bir maksimum ve bir minimumun olduğunu belirtir ancak bu noktaların değerlerini hesaplamanın bir faydası yoktur.

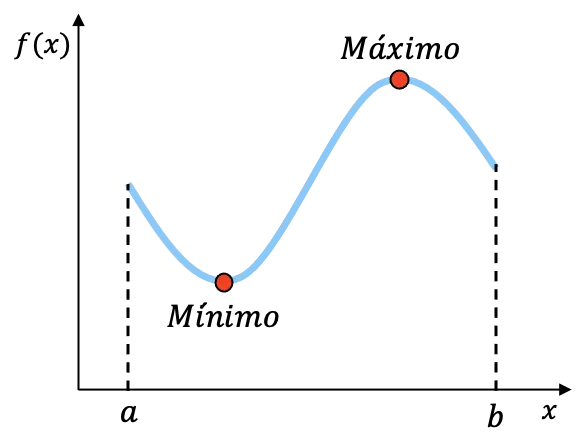
Örneğin, yukarıda grafiği çizilen fonksiyon [a,b] aralığında süreklidir ve bu aralıkta bir minimum ve bir maksimuma sahiptir. Bu iki noktanın tam koordinatlarını bilemesek de fonksiyonun aralıkta bu iki uç noktaya sahip olduğunu biliyoruz.

➤ Bakınız: bir fonksiyonun maksimum ve minimumunun nasıl hesaplanacağı

Fonksiyon tüm aralık boyunca sürekli olduğundan, bu aynı aralıkta mutlak minimum ile mutlak maksimum arasındaki olası tüm değerleri de alacağı anlamına gelir.

Ayrıca Weierstrass teoreminin bir sonucu olarak, kapalı bir aralıktaki herhangi bir sürekli fonksiyonun yukarıdan ve aşağıdan sınırlı olduğu ve fonksiyonun üst ve alt sınırlarının sırasıyla mutlak maksimum ve minimum olduğu sonucuna varılabilir.

Matematiksel olarak Weierstrass teoremi şu şekilde ifade edilebilir:

Altın

Ve

kapalı aralıkta yer alan iki noktadır (sırasıyla mutlak minimum ve mutlak maksimum)

fonksiyonun tanımlandığı yer.

Weierstrass teoreminin ispatı oldukça karmaşık olup kavrama pek bir katkısı olmadığından bu yazıda açıklamayacağız. Önemli olan Weierstrass teoreminin ne olduğunu ve ne için kullanıldığını anlamanızdır.

Weierstrass Teoremi Çözülmüş Sorunlar

1. Egzersiz

Aşağıdaki fonksiyonun önerilen aralıkta sınırlı olup olmadığını belirleyin:

➤ Bakınız: logaritmik bir fonksiyonun tanım kümesi

Weierstrass teoremini uygulayarak fonksiyonun [5,10] aralığında sınırlı olup olmadığını belirleyebiliriz. Bu nedenle fonksiyonun bu aralıkta sürekli olup olmadığını bilmemiz gerekir; bunu yapmak için logaritmik fonksiyonun tanım kümesini hesaplarız:

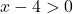
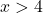
Fonksiyon x=4’ten büyük tüm değerler için süreklidir, yani [5,10] aralığında süreklidir.

Dolayısıyla fonksiyon [5,10] aralığında Weierstrass teoremini karşılar, yani bu aralığın üstünden ve altından sınırlanmıştır.

Alıştırma 2

Aşağıdaki fonksiyonun önerilen aralıkta maksimum ve/veya minimuma sahip olup olmadığını belirleyin:

➤ Bakınız: rasyonel bir fonksiyonun alanı

İlk olarak rasyonel fonksiyonun sürekliliğini analiz ediyoruz:

Ancak fonksiyon x=2’de bir süreksizlik gösterir, bu da onun [-3,3] aralığında sürekli olmadığını gösterir.

Kısacası fonksiyon Weierstrass teoremini sağlamadığından bu aralıkta minimumu veya maksimumu olup olmadığını söyleyemeyiz.

Alıştırma 3

Aşağıdaki fonksiyonun önerilen aralıkta maksimum ve/veya minimuma sahip olup olmadığını belirleyin ve bu noktaları hesaplayın:

➤ Bakınız: ikinci dereceden fonksiyonların özellikleri

Herhangi bir ikinci dereceden fonksiyonun tanım kümesinin tamamı gerçek sayılardır:

Dolayısıyla fonksiyon [0,4] aralığında süreklidir ve Weierstrass teoremini karşılar. Dolayısıyla fonksiyonun bu aralıkta mutlak bir minimumu ve mutlak bir maksimumu vardır.

Ayrıca, bu parabolün tepe noktası tam olarak x=0’dadır, dolayısıyla fonksiyon [0,4] aralığında kesin olarak artmaktadır ve sonuç olarak minimum x=0’da ve maksimum x= 4’tedir.

Karl Weierstrass

Weierstrass teoreminin ne anlama geldiğini gördükten sonra bu teoremin envanterinin kim olduğunu kısaca açıklayacağız.

Karl Theodor Wilhelm Weierstrass, 19. yüzyılda çok önemli bir Alman matematikçiydi, daha doğrusu 31 Ekim 1815’te Ostenfelde’de doğdu ve 19 Şubat 1897’de Berlin’de öldü.

Weierstrass teoreminin yanı sıra matematiğe yaptığı diğer katkılarla da tanınmaktadır. Bunlar arasında fonksiyonların çok önemli üç kavramı olan süreklilik, limit ve türevin tanımlarını verdi.

Aynı şekilde Bolzano-Weierstrass teoremi, ortalama değer teoremi veya Heine-Borel teoremi gibi o dönemde henüz matematiksel olarak doğrulanmamış bazı teoremleri göstermeyi başardı.

İlginç bir şekilde, bir ay krateri ve onun onuruna Weierstrass’ın adını taşıyan bir asteroit var.