Bu yazıda sınırlı (üst ve alt) fonksiyonların ne olduğunu açıklıyoruz. Ek olarak, size bir fonksiyonun bir noktada sınırlı olmasının ne anlama geldiğini göstereceğiz ve son olarak bu tip fonksiyonun özelliklerini bulacaksınız.
Sınırlı fonksiyon nedir?
Sınırlı bir fonksiyon, grafiği sınırlar içinde olan bir fonksiyondur. Yani, bir fonksiyon, eğer fonksiyonun K’den (f(x)≤K) daha büyük bir değeri olmayacak şekilde bir K sayısı varsa, yukarıdan sınırlıdır ve bir fonksiyon, eğer bir K sayısı varsa, aşağıdan sınırlıdır. (f(x)≥K) fonksiyonunun tüm değerlerinden küçüktür. Bu nedenle sınırlı bir fonksiyon, yukarıdan ve aşağıdan sınırlı olan bir fonksiyondur.
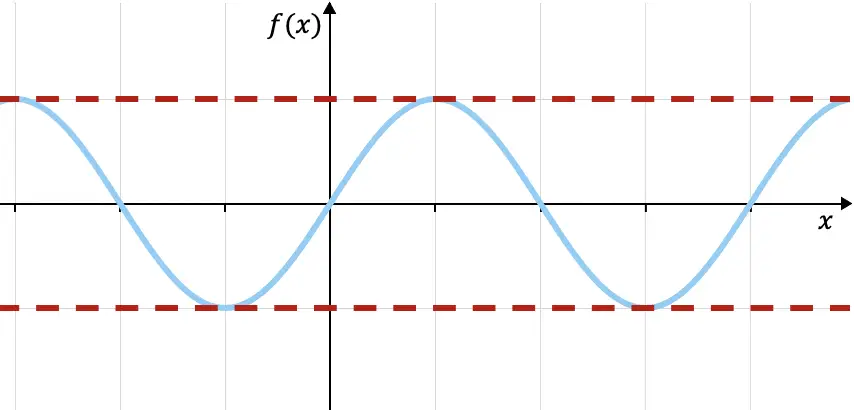
Örneğin, yukarıda grafiği gösterilen trigonometrik sinüs fonksiyonu üstte f(x)=1 ile, altta ise f(x)=-1 (kırmızı noktalı çizgiler) ile sınırlanmıştır, çünkü fonksiyonu bu iki limit dahilindedir. Bu işlevin daha fazla özelliğini aşağıdaki bağlantıda görebilirsiniz:
➤ Bakınız: Sinüs fonksiyonunun özellikleri
yukarıda sınırlı fonksiyon
Ancak tüm fonksiyonlar yukarıdan ve aşağıdan sınırlı değildir; bir fonksiyon yalnızca yukarıdan veya aşağıdan sınırlanabilir.
Yukarıda sınırlanan işlevler, belirli bir değeri aşmayan, yani aşağıdaki koşulu karşılayan işlevlerdir:
![]()
burada K değeri fonksiyonun üst sınırıdır.
Örneğin, aşağıdaki parabolün üst kısmı K=7 ile sınırlıdır, ancak dalları sonsuza kadar uzandığı için fonksiyon alttan sınırlı değildir.

Mantıksal olarak eğer fonksiyon K=7 ile sınırlıysa, aynı zamanda K=8 ve daha yüksek değerlerle de sınırlıdır.
En küçük üst sınıra üst sınır denir ve sup(f) ile temsil edilir. Ayrıca fonksiyon kendi tanım kümesinde söz konusu üst sınıra ulaşırsa bu noktanın fonksiyonun mutlak maksimumu olduğunu söyleyeceğiz.
➤ Bakınız: bir fonksiyonun maksimum ve minimumları nelerdir?
Bizim durumumuzda fonksiyon geometrik olarak K=7 ile sınırlıdır, dolayısıyla fonksiyonun üst uç noktası ve mutlak maksimumudur.
aşağıda sınırlandırılmış işlev
Aşağıda sınırlandırılan işlevler, değeri belirli bir sayıdan küçük olmayan, yani aşağıdaki matematiksel ifadeyi sağlayan işlevlerdir:
![]()
Burada K değeri fonksiyonun alt sınırıdır.
Aşağıda, K=3 ile sınırlandırılan bir üstel fonksiyonun grafiksel temsili bulunmaktadır:

Açıkçası, fonksiyon aynı zamanda K=3’ten küçük değerlerle de sınırlıdır.
Daha önce olduğu gibi en büyük alt sınıra alt sınır denir ve inf(f) ile temsil edilir. Ayrıca, eğer fonksiyon kendi tanım kümesinde söz konusu alt uca ulaşırsa, bu noktanın fonksiyonun mutlak minimumu olduğunu söyleyeceğiz.
Bu durumda K=3 fonksiyonun mutlak minimumu değildir çünkü fonksiyon bu değere sonsuzda ulaşır ve dolayısıyla tanım kümesinin dışındadır. Başka bir deyişle f(x)=3, fonksiyonunun yatay bir asimptotudur .
Bir fonksiyonun grafik gösterimi olmadan üstten ve alttan sınırlı olup olmadığını bilmenizi sağlayan bir teorem vardır. Weierstrass teoreminin ne olduğunu görmek için buraya tıklayın.
➤ Bakınız: Weierstrass teoremi
Fonksiyon bir noktada sınırlı
Bir fonksiyonun sınırlandırılması kavramını az önce genel olarak inceledik, ancak bir fonksiyonun daha küçük bir komşulukta, yani fonksiyonun bir bölümünde sınırlı olup olmadığını analiz etmek de mümkündür.
Evet
![]()
fonksiyonun tanım kümesinde bir noktadır ve
![]()
Herhangi bir değerde, fonksiyonun bu noktada yukarıdan/aşağıdan sınırlı olduğunu söyleyeceğiz.
![]()
bir ortam varsa
![]()
fonksiyonun yukarıdan/aşağıdan sınırlandığı yer.
Bu nedenle, bir fonksiyon bu noktada sınırlıdır
![]()
bir mahallede üstten ve alttan sınırlandırılmışsa
![]()
Açıkçası, eğer bir fonksiyon genel olarak sınırlıysa, her noktasında da sınırlı olacaktır. Ancak bunun tersi yanlıştır, yani bir fonksiyonun her noktasından sınırlı olabileceği ve tüm tanım kümesi boyunca sınırlı olamayacağı anlamına gelir.
Örneğin, aşağıdaki afin fonksiyon her noktasında kısmen sınırlıdır, ancak sınırlı bir fonksiyon değildir.

Sınırlı fonksiyonların özellikleri
Sınırlı işlevler aşağıdaki özelliklere sahiptir:
- Evet

Ve

iki sınırlı fonksiyondur, iki fonksiyonun toplanması (veya çıkarılması)
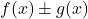
aynı zamanda sınırlı bir fonksiyondur.
- Evet

Ve

iki sınırlı fonksiyondur, iki fonksiyonun çarpımı
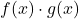
aynı zamanda sınırlı bir fonksiyondur.
- Bir fonksiyonun dikey asimptotu varsa tamamen sınırlanamaz. Öte yandan, fonksiyon yukarıdan veya aşağıdan sınırlanabilir.
- Bir aralıktaki herhangi bir sürekli ve sınırlı fonksiyon integrallenebilirdir.