Hiperbolik sinüs fonksiyonu

Bu makalede hiperbolik sinüs hakkında her şeyi bulacaksınız: formülü nedir, grafiksel gösterimi, tüm özellikleri, diğer fonksiyonlarla ilişkileri,…

Hiperbolik sinüs formülü

Hiperbolik sinüs fonksiyonu ana hiperbolik fonksiyonlardan biridir ve sinh(x) veya sinh(x) sembolüyle temsil edilir. Hiperbolik sinüs e ^x eksi e ^-x bölü 2’ye eşittir.

Hiperbolik sinüsün formülü bu nedenle aşağıdaki gibidir:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

Dolayısıyla hiperbolik sinüs üstel fonksiyonla ilişkilidir.

➤ Bakınız: üstel fonksiyonun özellikleri

Hiperbolik sinüsün grafiksel gösterimi

Önceki bölümde gördüğümüz formülü kullanarak hiperbolik sinüs değerlerinin bir tablosunu oluşturabilir ve fonksiyonun grafiğini çizebiliriz:

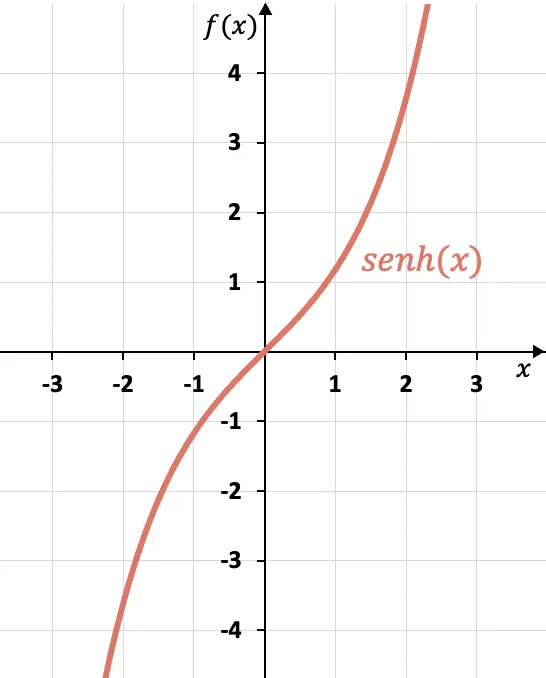
Bu grafikte hiperbolik sinüsün tek bir fonksiyon olduğunu görebiliriz, çünkü karşıt x’lerin zıt görüntüleri vardır, başka bir deyişle hiperbolik sinüs grafiği (0, 0) koordinatlarının orijinine göre simetriktir.

Gördüğünüz gibi hiperbolik sinüs grafiği, periyodik bir fonksiyon olan sinüs grafiğinden çok farklıdır. Aşağıdaki bağlantıda sinüsün grafiksel gösterimini ve hiperbolik sinüs ile tüm farklarını görebilirsiniz:

➤ Bakınız: Sinüs fonksiyonunun grafiksel gösterimi

Hiperbolik sinüsün özellikleri

Hiperbolik sinüs aşağıdaki özelliklere sahiptir:

Hiperbolik sinüs fonksiyonunun alanının tamamı gerçek sayılardır:

$\text{Dom } f = \mathbb{R}$

Hiperbolik sinüs fonksiyonunun aralığı veya aralığı da tamamen gerçek sayılardır.

$\text{Im } f= \mathbb{R}$

Hiperbolik sinüs sürekli ve tek bir fonksiyondur.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

X eksenini ve Y eksenini aynı kesişme noktasında, koordinat başlangıç noktasında keser:

$(0,0)$

X artı/eksi sonsuza yöneldiğinde hiperbolik sinüs fonksiyonunun limiti artı/eksi sonsuza eşittir:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

Hiperbolik sinüs etki alanı boyunca kesinlikle artmaktadır, dolayısıyla ne maksimumu ne de minimumu vardır.

Ancak x = 0 noktasında eğriliği değişir, dolayısıyla fonksiyonun dönüm noktasıdır. x=0’dan küçük değerler için içbükey fonksiyon, x=0’dan büyük değerler için ise dışbükey fonksiyondur.

Hiperbolik sinüs fonksiyonunun türevi hiperbolik kosinüstür:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Benzer şekilde hiperbolik sinüs fonksiyonunun integrali hiperbolik kosinüstür:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

Hiperbolik sinüs fonksiyonunun Taylor serisi aşağıdaki ifadeye eşdeğerdir:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

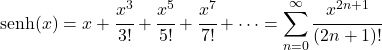
Hiperbolik sinüs fonksiyonunun Laplace dönüşümü aşağıdaki gibidir:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Hiperbolik sinüsün matematiksel ilişkileri

Hiperbolik sinüs diğer hiperbolik fonksiyonlara aşağıdaki denklemlerle bağlanır:

Temel denklem hiperbolik sinüsü hiperbolik kosinüsle ilişkilendirir:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Bu nedenle hiperbolik sinüs ve kosinüs fonksiyonları, x ² -y ² =1 olan hiperbol denklemiyle ilişkilidir. Daire denklemi (x ² +y ² =1) ile bağlanan trigonometrik sinüs ve kosinüs fonksiyonlarının aksine.

Sinüs, kosinüs ve tanjantın hiperbolik fonksiyonları aşağıdaki denklemle ilişkilendirilebilir:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Öte yandan iki farklı sayının toplanması veya çıkarılmasının hiperbolik sinüsü aşağıdaki formüllerle hesaplanabilir:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

Bir sayının iki katının hiperbolik sinüsü aşağıdaki matematiksel ilişki uygulanarak belirlenebilir:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

İki hiperbolik sinüsün toplamı veya çıkarılması aşağıdaki formüller kullanılarak bulunabilir:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Son olarak hiperbolik sinüsün karesi aşağıdaki formül uygulanarak hesaplanabilir:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Hiperbolik sinüs formülü

Hiperbolik sinüsün grafiksel gösterimi

Hiperbolik sinüsün özellikleri

Hiperbolik sinüsün matematiksel ilişkileri

Yorum bırakın Yanıtı iptal et