Teğet fonksiyonu - Mathority

Bu sayfada teğet fonksiyonu hakkında her şeyi bulacaksınız: nedir, formülü nedir, grafikte nasıl gösterilir, fonksiyonun özellikleri, periyodu vb. Ek olarak, kavramı tam olarak anlamak için teğet fonksiyon örneklerini görebileceksiniz. Hatta teğet teoremini ve teğet fonksiyonunun diğer trigonometrik ilişkilerle olan ilişkilerini bile açıklıyor.

Teğet fonksiyon formülü

Bir α açısının teğet fonksiyonu , formülü bir dik üçgenin (dik açılı üçgen) karşı dal ile bitişik (veya bitişik) dalı arasındaki oran olarak tanımlanan trigonometrik bir fonksiyondur.

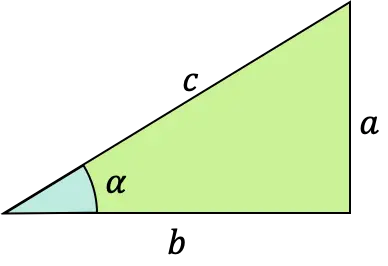
Bu tür matematiksel fonksiyona aynı zamanda teğetsel, tangenoid veya teğetsel fonksiyon da denir. Ve “tg”, hatta “tan” kısaltmasıyla da ifade edilebilir.

Teğet fonksiyonu, bir açının sinüsü ve kosinüsüyle birlikte en iyi bilinen üç trigonometrik orandan biridir.

Teğet fonksiyonunun karakteristik değerleri

Sık sık tekrarlanan belirli açılar vardır ve bu nedenle bu açılardaki teğet fonksiyonunun değerini bilmek uygundur:

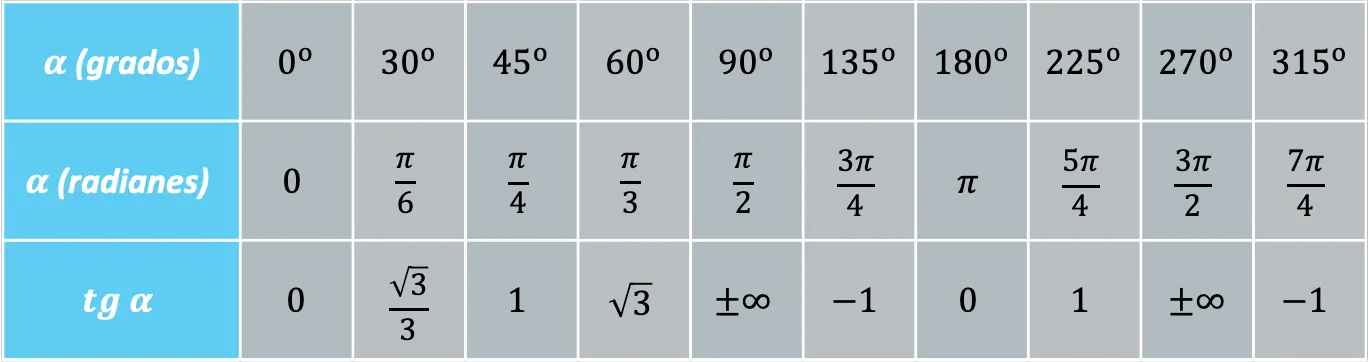
Öte yandan, teğet fonksiyonu sinüs ve kosinüs fonksiyonlarına aşağıdaki temel trigonometrik özdeşlik ile bağlanabilir:

$\text{tg } \alpha = \cfrac{\text{sen }\alpha}{\text{cos }\alpha}$

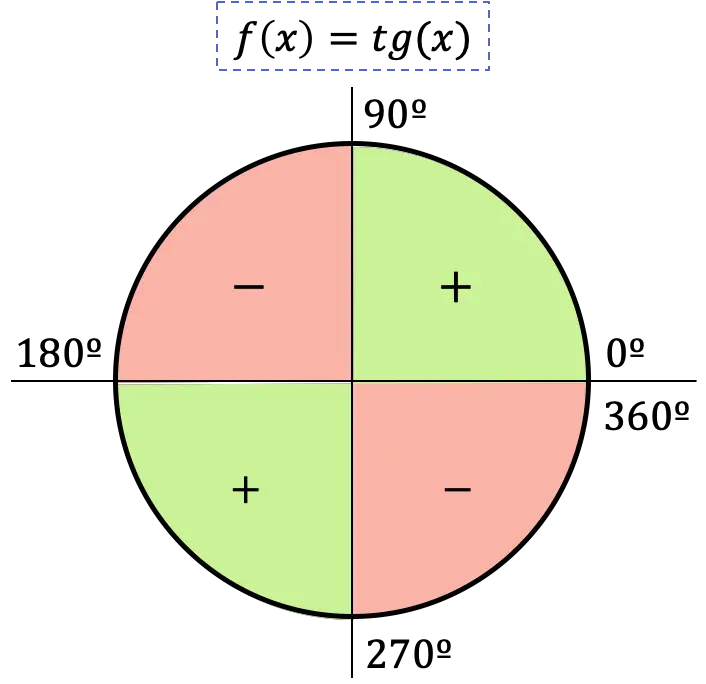
Dolayısıyla teğet fonksiyonunun işareti, açının bulunduğu çeyreğe bağlıdır:

Açı ilk çeyreğe aitse tanjantı pozitif olacaktır çünkü bu çeyrekte sinüs ve kosinüs de pozitiftir.
Açı ikinci çeyreğe düşerse tanjantı negatif olacaktır çünkü bu çeyrekte sinüs pozitif, kosinüs negatiftir.
Açı üçüncü çeyrekte ise tanjantı pozitif olacaktır çünkü bu çeyrekte sinüs ve kosinüs negatiftir.
Açı dördüncü çeyrekteyse tanjantı negatif olacaktır, çünkü bu çeyrekte sinüs negatif, bunun yerine kosinüs pozitiftir.

Teğet fonksiyonunun grafiksel gösterimi

Önceki bölümde gördüğümüz değerler tablosuyla teğet fonksiyonunun grafiğini çizebiliriz. Teğet fonksiyonunun grafiğini çizerek şunu elde ederiz:

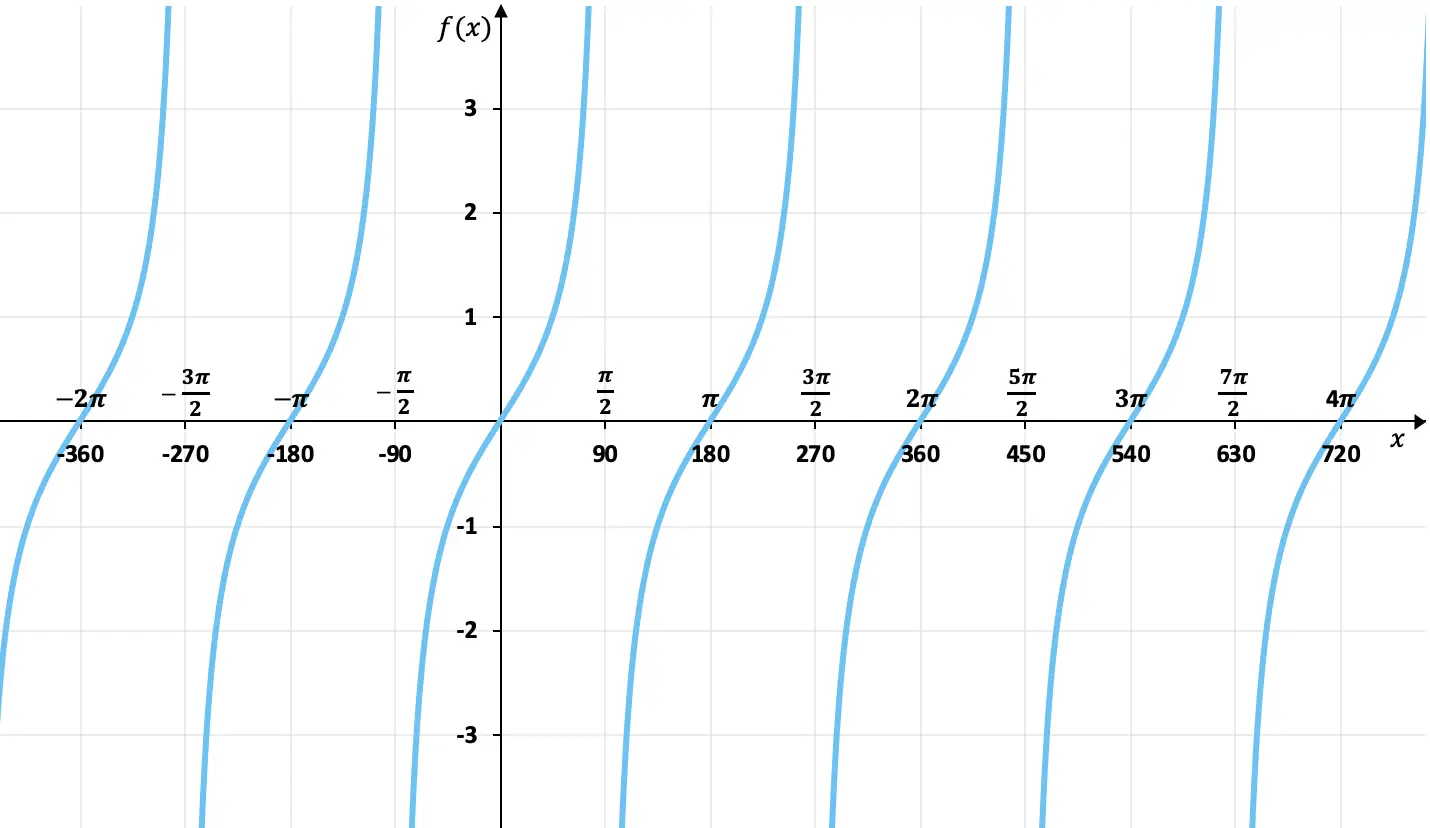
Grafikten de görebileceğiniz gibi teğet fonksiyonunun görüntülerinin değerleri sinüs ve kosinüs fonksiyonlarından farklı olarak sınırlı değildir. Ayrıca değerler her 180 derecede (π radyan) tekrarlanır, dolayısıyla periyodu 180° olan periyodik bir fonksiyondur .

Öte yandan bu grafikte teğet fonksiyonunun tek olduğunu görüyoruz çünkü karşıt elemanları zıt görüntülere sahip, yani orijine göre simetrik (0,0). Örneğin 45°’nin tanjantı 1, -45°’nin tanjantı -1 değerindedir.

Son olarak, teğet fonksiyonunun dikey asimptotlara sahip olduğunu da görebiliriz. Mesela x=90° çizgisine çok yaklaşıyor ama hiç dokunmuyor ve her 180 derecede bir aynı şey oluyor. Bu, fonksiyonun bu noktalardaki limitinin sonsuza doğru gittiği anlamına gelir.

Teğet fonksiyonunun özellikleri

Teğet fonksiyonu aşağıdaki özelliklere sahiptir:

Teğet fonksiyonunun alanı, dikey asimptotun olduğu noktalar dışındaki tüm gerçek sayılardır:

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{(2k+1)\cdot \frac{\pi}{2} \right\} \qquad k \in \mathbb{Z}$

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{\ldots \ , \ -\frac{\pi}{2} \ , \ \frac{\pi}{2} \ , \ \frac{3\pi}{2} \ , \ \ldots \right\}$

Teğet fonksiyonunun aralığı veya aralığının tümü gerçek sayılardır.

$\text{Im } f= \mathbb{R}$

Periyodikliği π olan sürekli ve tek bir fonksiyondur.

$\displaystyle \text{tg}(-x) =- \text{tg }x$

Bu tip trigonometrik fonksiyonun y ekseni (Y ekseni) ile (0,0) noktasında tek bir kesişme noktası vardır.

$(0,0)$

Bunun yerine periyodik olarak apsisi (X ekseni) pi’nin çeşitli koordinatlarında keser.

$\displaystyle (k\pi ,0) \qquad k \in \mathbb{Z}$

Fonksiyon tüm tanım kümesinde kesinlikle artmaktadır, dolayısıyla ne maksimumu ne de minimumu vardır.

Teğetin türevi:

$f(x)=\text{tg } x \ \longrightarrow \ f'(x)= 1+\text{tg}^2 x=\cfrac{1}{\text{cos}^2 x} =\text{sec}^2 x$

Son olarak teğet fonksiyonunun integrali:

$\displaystyle \int \text{tg } x \ dx= -\ln \lvert \text{cos }x \rvert + C$

Teğet fonksiyonunun periyodu

Sinüs ve kosinüs gibi diğer trigonometrik fonksiyonlardan farklı olarak tanjant fonksiyonunun büyüklüğü yoktur çünkü ne maksimum ne de minimum değeri vardır. Ancak periyodik bir fonksiyondur yani değerleri grafiğinde gördüğümüz gibi bir frekansla tekrar etmektedir.

$\displaystyle f(x)= \text{tg}(wx)$

Teğet fonksiyonunun periyodu , grafiğin tekrarlandığı iki nokta arasındaki mesafedir ve aşağıdaki formülle hesaplanır:

$\displaystyle \text{Periodo}=T=\cfrac{\pi}{w}$

teğet teoremi

Teğet formülü normalde dik üçgenlerde kullanılsa da, her tür üçgene uygulanacak bir teorem de vardır: teğet teoremi.

Teğet teoremi herhangi bir üçgenin kenarlarını ve açılarını şu şekilde ilişkilendirir:

$\displaystyle \cfrac{a+b}{a-b} = \cfrac{ \text{tg}\left(\frac{\alpha+\beta}{2}\right)}{\text{tg}\left(\frac{\alpha-\beta}{2}\right)}$

$\displaystyle \cfrac{a+c}{a-c} = \cfrac{ \text{tg}\left(\frac{\alpha+\gamma \vphantom{\beta}}{2}\right)}{\text{tg}\left(\frac{\alpha-\gamma\vphantom{\beta}}{2}\right)}$

$\displaystyle \cfrac{b+c}{b-c} = \cfrac{ \text{tg}\left(\frac{\beta+\gamma}{2}\right)}{\text{tg}\left(\frac{\beta-\gamma}{2}\right)}$

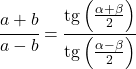
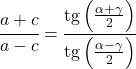
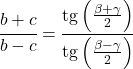
Teğet fonksiyonunun diğer trigonometrik oranlarla ilişkileri

Aşağıda tanjant ile trigonometrinin en önemli trigonometrik oranları arasındaki ilişkiler bulunmaktadır.

Meme ile ilişki

Bir açının tanjantı ve sinüsü aşağıdaki şekilde ilişkilidir:

$\displaystyle \text{tg }\alpha = \pm \cfrac{\text{sen }\alpha }{\sqrt{1-\text{sen}^2\alpha \vphantom{\bigl( }}}$

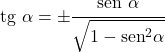
Kosinüs oranı

Benzer şekilde bir açının tanjantı ve kosinüsü aşağıdaki eşitlikle ilişkilidir:

$\displaystyle \text{tg }\alpha = \pm \cfrac{\sqrt{1-\text{cos}^2\alpha \vphantom{\bigl( }} }{\text{cos }\alpha}$

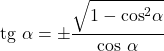
Kosekant ile ilişki

Kanıtlanması zor olsa da teğet, yalnızca kosekantına bağlı olacak şekilde çözülebilir:

$\displaystyle \text{tg }\alpha = \pm \cfrac{1}{\sqrt{\text{csc}^2\alpha -1 \vphantom{\bigl( }}}$

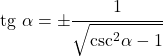
Sekant ile ilişki

Bir açının tanjantı ve sekantı aşağıdaki denklemle ilişkilidir:

$\displaystyle \text{tg }\alpha = \pm\sqrt{\text{sec}^2\alpha -1$

Kotanjant ile ilişki

Teğet ve kotanjant çarpımsal terslerdir:

$\displaystyle \text{tg }\alpha =\pm \cfrac{1}{\text{cot }\alpha}$

Teğet işlevi