Bu sayfada ters orantı fonksiyonlarının ne olduğu ve bunların grafiğinin nasıl çizileceği açıklanmaktadır. Ek olarak, bu tür bir fonksiyonun tüm özelliklerini, tanım kümesinin nasıl hesaplanacağını ve ayrıca uygulamaya yönelik adım adım çözülmüş çeşitli örnekleri ve alıştırmaları bulacaksınız.
Ters orantı fonksiyonu nedir?
Ters orantı fonksiyonu , iki ters orantılı niceliği ilişkilendiren bir fonksiyondur; yani bir nicelik artarken diğerinin azaldığını veya bunun tersinin olduğunu söyleriz. Genel olarak ters orantı fonksiyonları aşağıdaki formülle tanımlanır:
![]()
Altın
![]()
orantılılık oranı adı verilen bir sabittir.
Dolayısıyla ters orantı fonksiyonları her zaman paydasında birinci dereceden polinom bulunan kesirlerden oluşur. Bu nedenle bir tür rasyonel fonksiyondurlar.
Ters orantı fonksiyonlarına örnekler:
![]()
Genel olarak
![]()
genellikle bağımsız değişkendir ve
![]()
bağımlı değişken veya başka bir deyişle değişken
![]()
bağlıdır
![]()
Öte yandan orantı oranı (pay terimi) pozitif veya negatif olabilir ve işareti fonksiyondaki artışı veya azalışı gösterir:
- Eğer sabit

negatifse fonksiyon artıyor.
- Bunun yerine, eğer sabit

pozitifse fonksiyon azalmaktadır.
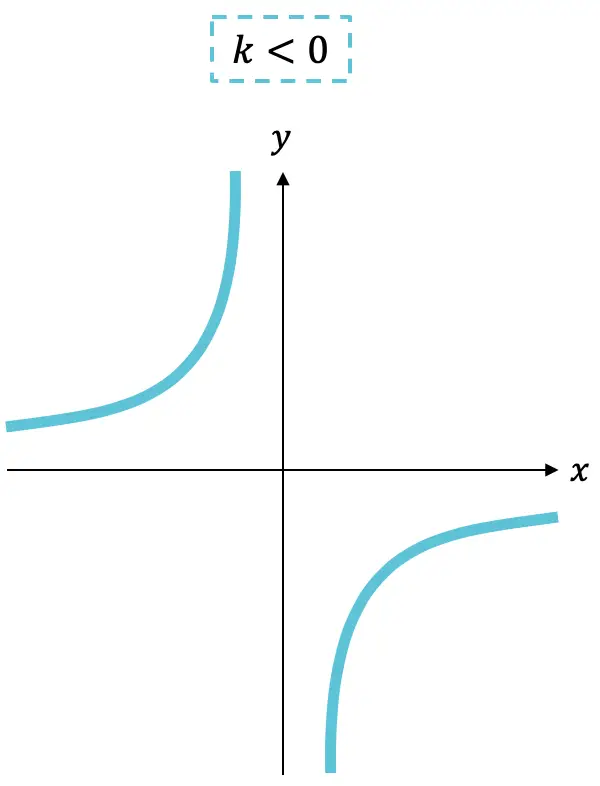
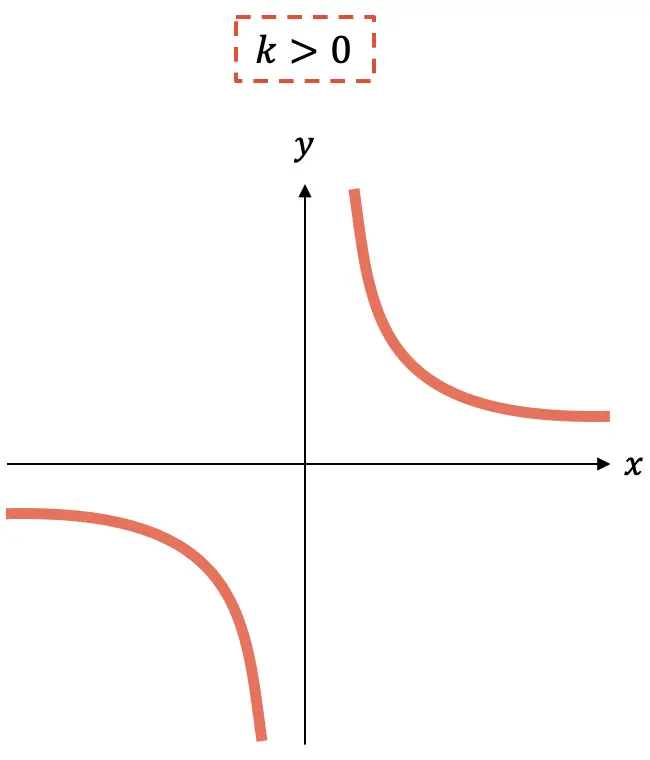
Gördüğünüz gibi, bir ters orantı fonksiyonunun grafiği her zaman k’nin işaretine bağlı olarak bir çeyrekte veya diğerinde olacak iki hiperbolden oluşur .
Ters orantı fonksiyonunun alanı
Bir rasyonel fonksiyon türü olan ters orantı fonksiyonunun alanı, paydada kaybolanlar dışındaki tüm gerçek sayılardır . Çünkü payda hiçbir zaman sıfır olamaz çünkü bu sonsuza neden olur.
Örnek olarak aşağıdaki ters orantı fonksiyonunun tanım kümesini belirleyeceğiz:
![]()
Paydanın ne zaman sıfır olduğunu bilmek için ifadesini 0’a eşitlemeli ve denklemi çözmeliyiz:
![]()
![]()
Böylece x 1 değerini aldığında payda sıfır olacak ve belirsizlik elde edeceğiz. Yani fonksiyonun tanım kümesi tüm gerçek sayılar eksidir
![]()
![]()
Ters Orantılılık Fonksiyonunun Grafiği Nasıl Çizilir
Bir örnek kullanarak ters orantı fonksiyonunun grafiğinin nasıl çizileceğini göreceğiz.
- Aşağıdaki fonksiyonu bir grafikte temsil edeceğiz:
![]()
Yapmamız gereken ilk şey fonksiyonun tanım kümesini bulmaktır. Kesir olduğundan payda hiçbir zaman 0 olamaz çünkü bu durumda sonsuzluğa neden olur. Bu nedenle, paydanın iptal edildiği durumlar dışında etki alanının tamamı x olacaktır.
Bu nedenle hangi x’in alana ait olmadığını görmek için paydayı 0’a eşitliyoruz:
![]()
![]()
Bu nedenle, fonksiyonun tanım kümesi 2 dışındaki tüm sayılardır:
![]()
Hangi sayının alana ait olmadığını öğrendikten sonra bir değerler tablosu oluştururuz. Ters orantı fonksiyonlarını temsil etmek için (2) alanına ait olmayan sayının solunda 3 veya 4, sağında 3 veya 4 puan hesaplamak gerekir:
![]()

Şimdi noktaları grafik üzerinde gösterelim :
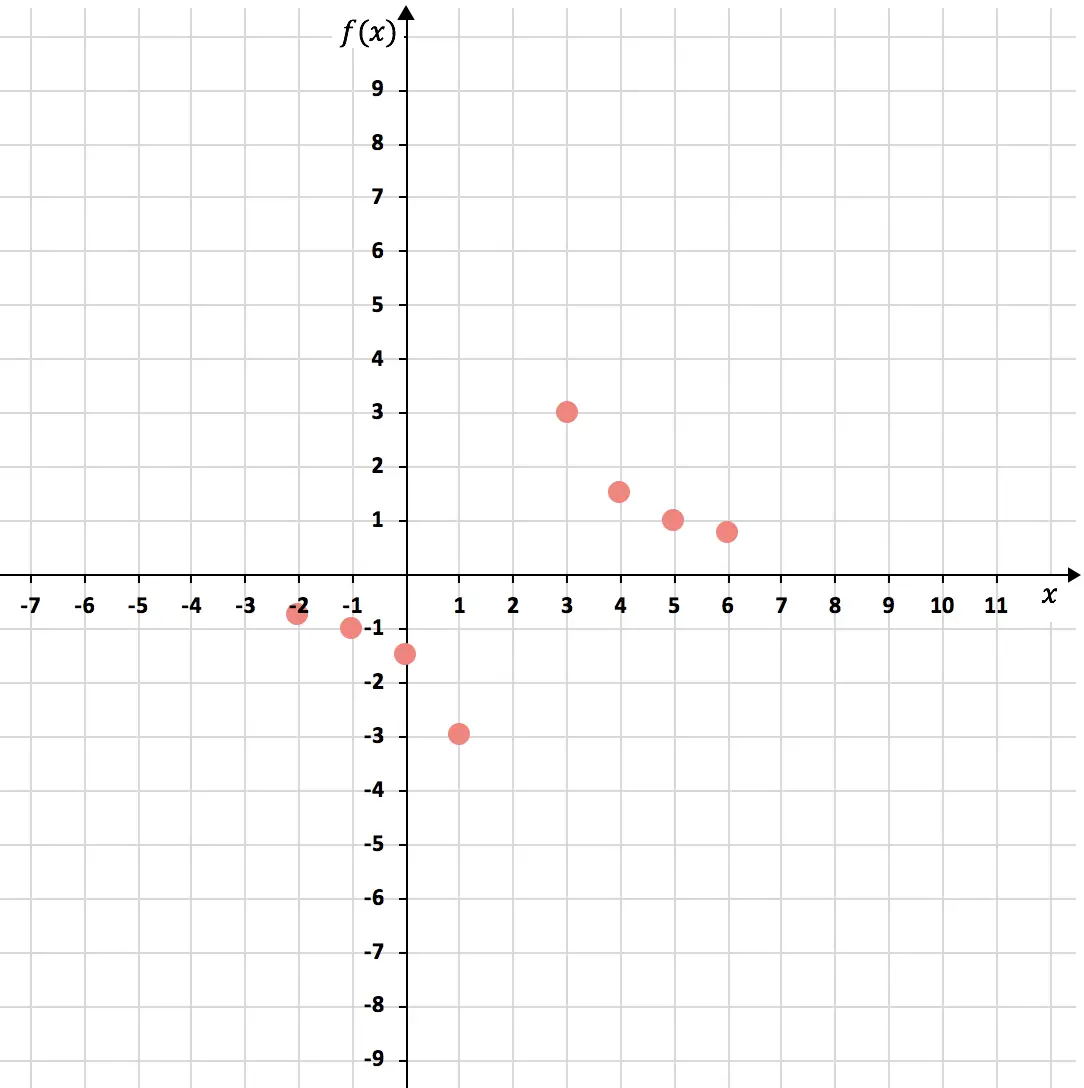
Ve son olarak ters orantı fonksiyonunun iki hiperbolünü oluşturarak noktaları birleştiriyoruz. Ek olarak hiperbollerin büyümeye devam ettiğini belirtmek için dallarını uzatıyoruz:

Fonksiyonun yaklaşık olduğunu unutmayın
![]()
, hem sağda hem de solda. Ancak asla 2’ye tam olarak ulaşamıyor, çok yaklaşıyor ama asla ulaşamıyor. BU YÜZDEN,
![]()
dikey bir asimptottur . Çünkü
![]()
fonksiyonun tanım kümesine ait değildir ve dolayısıyla fonksiyon o noktada mevcut değildir.
Aynı şey yatay X ekseninde de oluyor. Fonksiyon yaklaşıktır
![]()
ama asla dokunmayın. Henüz,
![]()
yatay bir asimptottur .
Bu, tüm ters orantı fonksiyonlarının süreksiz olduğu anlamına gelir çünkü bunların her zaman bir asimptotu vardır.
Asimptotlar ve fonksiyonların limitleri hakkında daha fazla bilgiyi web sitemizden edinebilirsiniz.
Ters orantı fonksiyonlarının çözülmüş problemleri
1. Egzersiz
Aşağıdaki ters orantı fonksiyonunun tanım kümesini hesaplayın:
![]()
Payda 0 olduğunda ters orantı fonksiyonu mevcut olmayacaktır çünkü o zaman fonksiyon ∞ sonucunu verecektir. Bu nedenle, x’in paydayı iptal ettiğini ve dolayısıyla tanım kümesine ait olmadığını görmek için fonksiyonun paydasını 0’a eşitlememiz gerekir.
![]()
![]()
![]()
![]()
Alıştırma 2
Aşağıdaki ters orantı fonksiyonunun grafiğini çizin:
![]()
Yapılacak ilk şey fonksiyonun tanım kümesini hesaplamaktır:
![]()
![]()
Hangi sayının alana ait olmadığını öğrendikten sonra aşağıdaki fonksiyonla bir değerler dizisi oluştururuz:

Son olarak elde edilen noktaları grafikte temsil edip hiperbolleri çizerek ters orantı fonksiyonunu oluşturuyoruz:
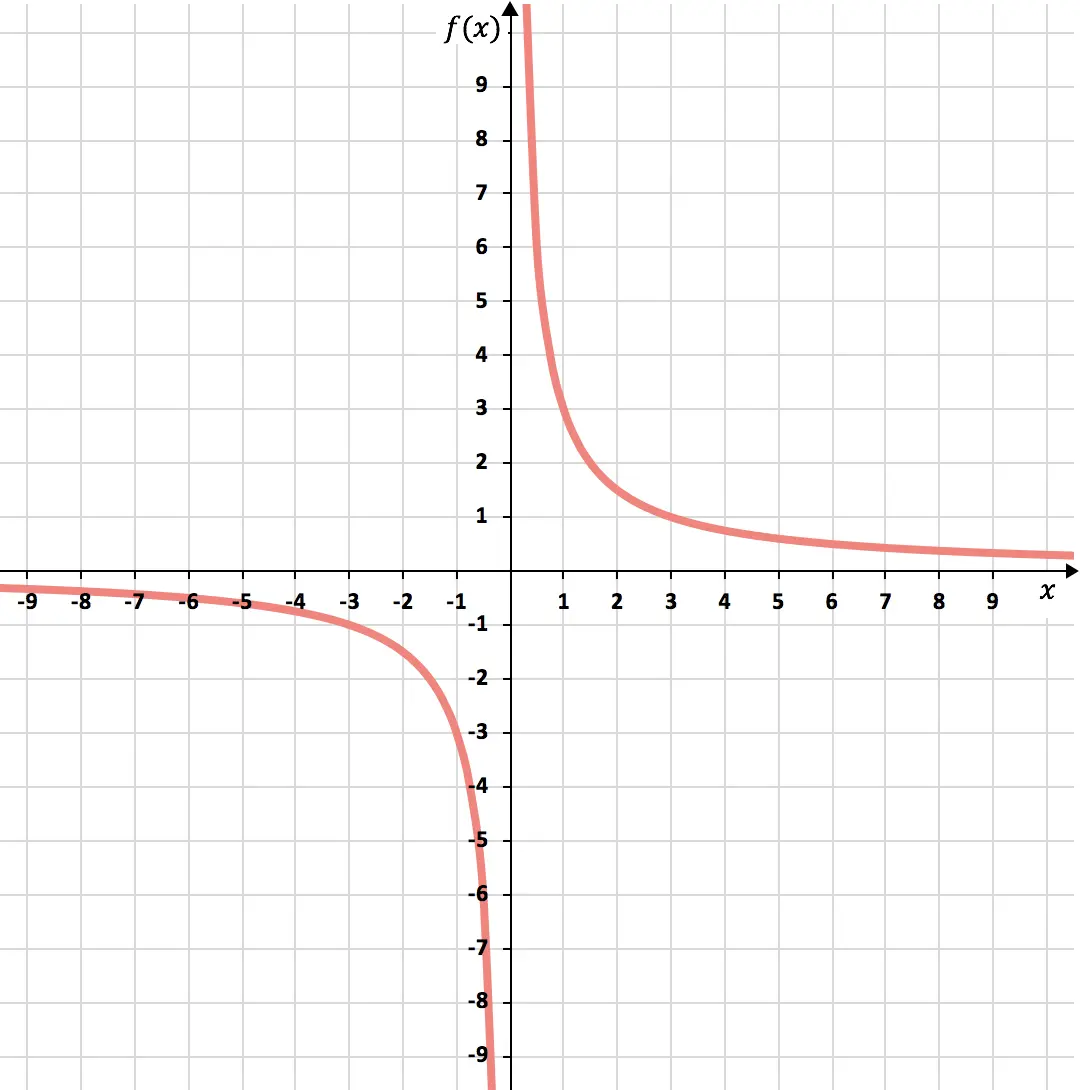
Alıştırma 3
Aşağıdaki ters orantı fonksiyonunun grafiğini çizin:
![]()
Yapılacak ilk şey fonksiyonun tanım kümesini hesaplamaktır:
![]()
![]()
![]()
Fonksiyonun tanım kümesini öğrendikten sonra bir değerler tablosu oluştururuz:

Son olarak, elde edilen noktaları bir grafik üzerinde temsil ediyoruz ve hiperbolleri çiziyoruz, böylece ters orantı fonksiyonunu oluşturuyoruz:
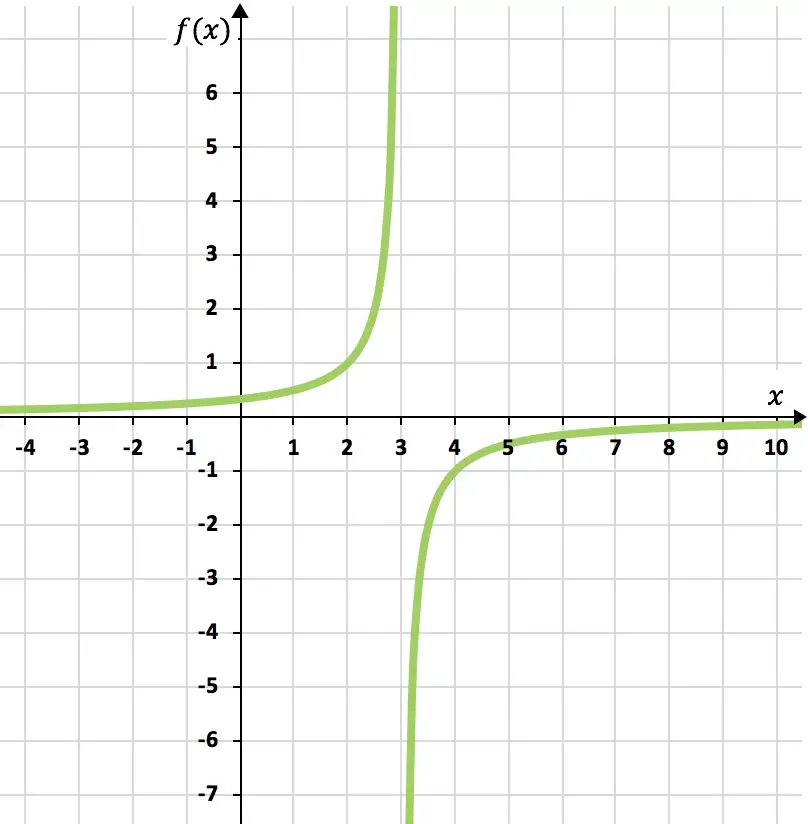
Alıştırma 4
Aşağıdaki ters orantı fonksiyonunun grafiğini çizin:
![]()
Öncelikle fonksiyonun tanım kümesini hesaplamamız gerekir:
![]()
![]()
![]()
![]()
Fonksiyonun tanım kümesini öğrendikten sonra bir değerler dizisi yaratırız:
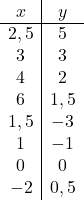
Ve son olarak elde edilen noktaları bir grafikte temsil ediyoruz ve hiperbolleri çizerek ters orantı fonksiyonunu oluşturuyoruz:
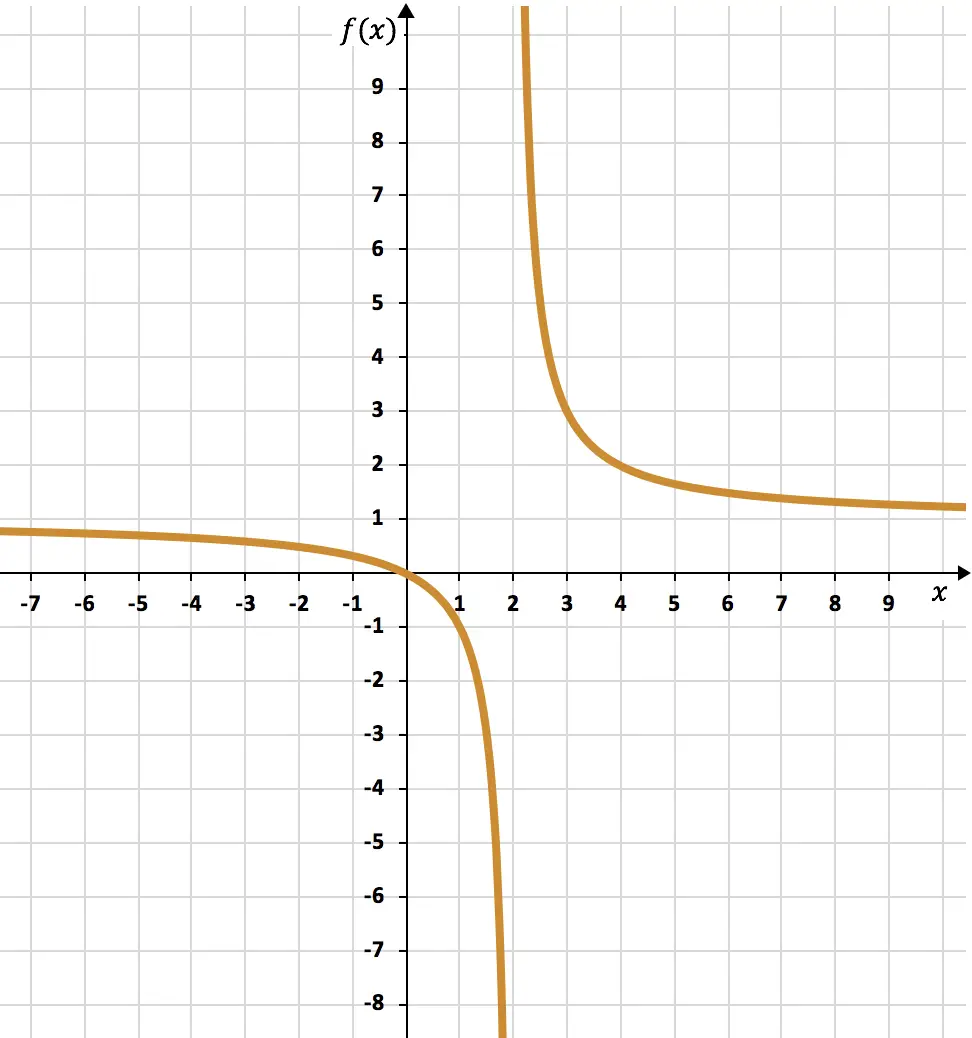
Alıştırma 5
Aşağıdaki rasyonel fonksiyonun grafiğini çizin:
![]()
Yapılacak ilk şey fonksiyonun tanım kümesini hesaplamaktır:
![]()
![]()
![]()
![]()
Fonksiyonun tanım kümesini öğrendikten sonra bir değerler tablosu oluştururuz:

Bitirmek için, elde edilen noktaları bir grafikte temsil edin ve hiperbolleri çizin, böylece kesirli fonksiyonu oluşturun:

Ters orantı fonksiyonunun uygulamaları
Ters orantı fonksiyonu fizik ve matematikte birçok durumda karşımıza çıkar.
Örneğin sabit bir k sıcaklığına maruz kalan ideal bir gazdaki basınç ve hacim arasındaki ilişkiyi tanımlamak için kullanılır. Bu fonksiyona Boyle-Mariotte yasası (P×V=k) adı verilir ve ters orantı fonksiyonunun bir örneğidir. Açıkçası, bu fonksiyonun tanım alanı yalnızca pozitif dalla sınırlıdır, çünkü negatif hacim veya basınç yoktur.
Akım yoğunluğu ile sabit potansiyel farkına maruz kalan elektrik direnci arasındaki ilişki de ters orantı fonksiyonu tarafından yönetilir. Bu fonksiyon Ohm kanunu (V=I×R) olarak bilinir.