Bu sayfada üstelsıfır matrisin ne olduğuna dair bir açıklamanın yanı sıra onu anlayabilmeniz ve hiçbir şüphe duymamanız için birkaç örnek bulacaksınız. Ayrıca üstelsıfır matrislerin yapılarını ve bu tür matrislerin tüm özelliklerini görebileceksiniz.
Üstelsıfır matris nedir?
Nilpotent matrisin tanımı aşağıdaki gibidir:
Üstelsıfır matris, sıfır matrisini veren bir tamsayıya yükseltilen bir kare matristir.
![]()
Altın
![]()
üstelsıfır matristir ve
![]()
sıfır matrisini veren kuvvetin üssü.
Bu durum, üstelsıfır bir matrisin kuvvetinin üssü ne olursa olsun her zaman sıfır vereceği anlamına gelmez; bunun yerine, sonucu 0’larla dolu bir matris olan matrisin en az bir kuvveti varsa, o zaman matrisin üstelsıfır olduğu anlamına gelir.
Öte yandan, üst düzey bir matrisin üst düzey güç indeksi , üst düzey güç koşulunun sağlandığı en küçük sayıdır. Üstelsıfır matrisinin k düzeyinde olduğunu da söyleyebiliriz; burada k , onun üstgüç indeksidir.
Üstelsıfır matris örnekleri
Üstelsıfır matris kavramını anlamayı tamamlamak için, bu tür matrislerin birkaç örneğini göreceğiz:
2 × 2 üstelsıfır matris örneği
Aşağıdaki 2×2 boyutlu kare matris üstelsıfırdır:
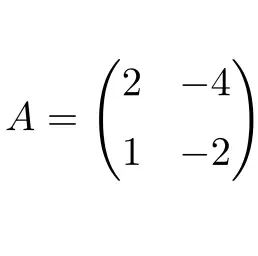
Matris üstelsıfırdır çünkü A matrisinin karesini alarak sıfır matrisini elde ederiz:
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fde370dd31b0e2a533fdf1e9d23cf2c9_l3.png)
Bu nedenle üstelsıfır bir matristir ve sıfır matrisin ikinci kuvveti elde edildiğinden üstlgüç indeksi 2’dir.
3×3 üstelsıfır matris örneği
Aşağıdaki 3. dereceden kare matris üstelsıfırdır:
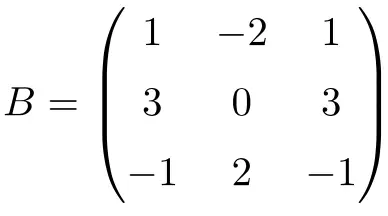
Matrisin 2’ye yükseltilmesine rağmen sıfır matrisini elde edemeyiz:
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbad4ccc270e2960ae50cc23eacc7530_l3.png)
Ancak matrisin küpünü hesaplarken tüm elemanları 0’a eşit olan bir matris elde ederiz:
![Rendered by QuickLaTeX.com \displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-da876a04b14d80c156e24c95bd22372e_l3.png)
Yani B matrisi üstelsıfır bir matristir ve sıfır matrisi 3’ün kuvvetine göre elde edildiğinden üstelgüç indeksi 3’tür.
2 × 2 üstelsıfır matrisin yapısı
Aşağıda tüm üstelsıfır matrislerin yapısını görebilirsiniz. Kanıtı biraz sıkıcı olduğundan sizi doğrudan 2. mertebeden üstelsıfır bir matris elde etmek için formülle baş başa bıraktık:
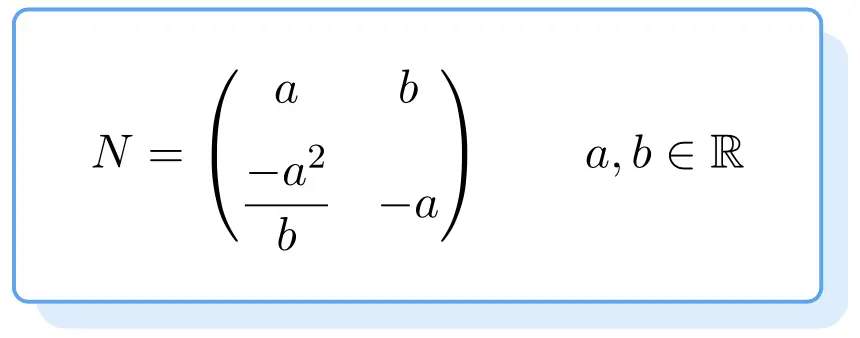
Yani yukarıdaki formülü karşılayan herhangi bir matris üstelsıfır bir matris olacaktır. Bunun için değerler
![]()
Ve
![]()
gerçek sayılar oldukları sürece keyfi olabilirler.
Üstelsıfır matrislerin özellikleri
Nilpotent matrisler aşağıdaki özelliklere sahiptir:
- Üstelsıfır bir matrisin izi her zaman sıfırdır.
- Benzer şekilde herhangi bir üstelsıfır matrisin determinantı her zaman 0’dır. Ancak bunun tersi doğru değildir, yani bir matrisin determinantının sıfır olması matrisin üstelsıfır olduğu anlamına gelmez.
- Köşegenleştirilebilen tek üstelsıfır matris sıfır matristir.
- n×n boyutlu bir üstelsıfır matrisin üstlgüç indeksi her zaman n’ye eşit veya ondan küçüktür. Bu nedenle 2 × 2 üstelsıfır matrisinin üstlsıfır indeksi her zaman 2 olacaktır.
- Nilpotent bir matris tersinir değildir.
- Ana köşegeninde sıfır bulunan herhangi bir üçgen matris aynı zamanda üstelsıfır bir matristir.
- Matrisin şöyle olduğunu söyleyen bir teorem vardır:

üstelsıfır ise matris
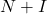
tersinirdir, burada
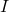
kimlik matrisidir. Ayrıca ters matrisi aşağıdaki formülle de bulunabilir:
![]()
- Eşdeğer olarak eğer

üstelsıfır bir matris ise matrisin tersi hesaplanabilir
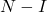
aşağıdaki denklemle:
![]()
- Herhangi bir tekil matris, yani tersinir olmayan, üstelsıfır matrislerin çarpımına ayrıştırılabilir.
- Üstelsıfır bir matrisin tüm özdeğerleri (veya özdeğerleri) sıfırdır.
![]()
- Son olarak merak olarak doğrusal bir uygulamayı tanımlayan üstelsıfır dönüşüm kavramı da var.
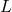
öyle bir vektör uzayının
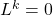
.