Burada her türlü önemli kimlik (veya önemli ürün) çözümünün açıklamasını bulacaksınız. Tüm önemli kimliklerin formüllerinin neler olduğunu, ayrıca adım adım çözülmüş örnekleri ve alıştırmaları görebileceksiniz. Ayrıca bu ünlü matematik kurallarının ne için kullanıldığını da göstereceğiz.
👉👉 Aşağıda her önemli kimliği adım adım açıklıyoruz, ancak isterseniz doğrudan tüm formüllerin özetlendiği tabloya 😉 gidebilirsiniz. 👈👈
Dikkate değer kimlikler (veya dikkate değer ürünler) nelerdir?
Dikkat çekici çarpımlar veya dikkate değer eşitlikler olarak da adlandırılan dikkat çekici özdeşlikler , polinomlarla yapılan işlemlerin doğrudan çözülmesine olanak sağlayan matematik kurallarıdır.
En yaygın dikkate değer özdeşlik formülleri , bir toplamın karesi , bir farkın karesi (veya çıkarma) ve toplam çarpı farktır .

Ancak aşağıda size yalnızca bu dikkate değer çarpımların nasıl hesaplanacağını öğretmekle kalmayıp, aynı zamanda var olan tüm dikkate değer kimlik türlerini de göstereceğiz.
Önemli kimlik formülleri (veya ürünleri)
Dikkate değer ürünlerin (veya dikkate değer eşitliklerin) tanımını gördükten sonra, dikkate değer kimliklerin formüllerinin ne olduğunu göreceğiz. Öte yandan formül demolarıyla ilgileniyorsanız, “demoyu görüntüle” butonlarına tıklayarak formülleri görüntüleyebilirsiniz.
bir toplamın karesi
Bir toplamın karesi veya toplamın karesi , en önemli kimliklerden biridir. Daha doğrusu, iki pozitif terim üssü 2 olan bir binomdur, yani cebirsel ifadesi (a+b) 2’dir .
Yani bir toplamın karesi formülü şu şekildedir:

2’ye yükseltilmiş pozitif bir binomdan başlarsak:
![]()
Matematiksel olarak yukarıdaki kare şu faktöre eşittir:
![]()
kendisi ile çarpılır:
![]()
Yani polinomları dağılma özelliğini kullanarak çarpıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Elde edilen dört terimden,
![]()
Ve
![]()
benzer görünmeleri için bunları gruplandırabiliriz:
![]()
Öyle ki, türetildiği kare toplam formülünün ifadesine zaten ulaşmıştık:
![]()
Merak konusu olarak, bu tür dikkat çekici bir ürün için ifadenin geliştirilmesine tam kare trinomial adı verilmektedir.
Yani bir toplamın karesi, birinci terimin karesi artı birinci terimin ikinci çarpımının iki katı artı ikinci terimin karesine eşittir.
Dolayısıyla kare toplamı çözmek için her toplamayı her ikisine birden yapmak yeterli değildir, ancak ek olarak iki toplamanın birbiriyle ve 2 ile çarpılması gerekir. Bunu hatırlamak önemlidir çünkü bu türden çok tipik bir hatadır. Ürünün bu terimi unutması dikkat çekicidir.

Örnek:
- İlgili formülü uygulayarak aşağıdaki dikkate değer kimliği hesaplayın:
![]()
Az önce gördüğümüz gibi, kareler toplamının kayda değer eşitliğinin formülü şöyledir:
![]()
Bu nedenle öncelikle parametreleri tanımlamamız gerekir.
![]()
Ve
![]()
formülü. Bu durumda,
![]()
temsil etmek
![]()
çiftin ve
![]()
5 numaraya karşılık gelir:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Artık değerlerini bildiğimize göre
![]()
ve
![]()
sonucu bulmak için kare pozitif binom formülünü kullanabiliriz:

farkın karesi
Bir farkın karesi veya farkın karesi , en çok kullanılan 3 önemli kimlikten bir diğeridir. Özellikle, bir pozitif terim ile 2’ye yükseltilmiş başka bir negatif terimden oluşan bir binom’a karşılık gelir, yani cebirsel ifadesi (ab) 2’dir .
Yani bir farkın karesi (veya bir çıkarmanın karesi) formülü aşağıdaki gibidir:

Kare çıkarmanın binom ifadesinden:
![]()
Açıkçası, önceki güç faktörün çarpımına eşittir
![]()
kendisi ile çarpılır:
![]()
Şimdi dağılma özelliğini uygulayarak iki parantezi çarpıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b46073fd758d93fff8956f0a8dd57af_l3.png)
Formülü kontrol etmeyi tamamlamak için benzer terimleri bir arada gruplamanız yeterlidir:
![]()
Daha sonra farkın karesi formülü matematiksel olarak kanıtlanır:
![]()
Yani bir farkın karesi, birinci terimin karesinden eksi birinci terimin ikinci çarpımının iki katı artı ikinci terimin karesine eşittir.
Toplamın karelerinin dikkat çekici eşitliğine gelince, aşağıdaki denklem yanlış olduğundan formülün orta terimini koymayı unutmamalıyız:

Örnek:
- Kare farkın aşağıdaki dikkate değer eşitliğini çözün:
![]()
Bu, kare çıkarmanın dikkate değer çarpımıdır, bu nedenle karşılık gelen formülünü uygulamak gerekir:
![]()
Daha sonra bilinmeyenlerin değerlerinin ne olduğunu belirlememiz gerekiyor.
![]()
Ve
![]()
formülü. Bu durumda,
![]()
değişken
![]()
Ve
![]()
3 numaraya karşılık gelir:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1bb2d14a30d2cdabae6458f5df32392a_l3.png)
Negatif işaretin parametrenin bir parçası olmadığını unutmayın
![]()
ancak bu formülü doğru bir şekilde uygulamak için her zaman işareti olmayan sayıyı almalısınız.
Bu nedenle değerlerini zaten biliyoruz.
![]()
ve
![]()
Bu nedenle, dikkate değer kimliği çözümlemek için bu değerleri formülde değiştirmek yeterlidir:

farka göre toplam
Bir toplamın ve bir farkın çarpımı en çok kullanılan 3 önemli kimlikten biridir. Adından da anlaşılacağı gibi, pozitif bir binomun eşlenik binomuyla (aynı binom ancak ara işareti değiştirilmiş) çarpımıdır, yani bu tür dikkat çekici çarpımın cebirsel ifadesi (a +b) · (ab) şeklindedir. .
Bir toplamın farkla çarpımının dikkat çekici özdeşliği için formül aşağıdaki gibidir:

Bir toplamın çarpımından herhangi iki terimin çıkarılmasıyla başlayarak:
![]()
Formülü göstermek için, dağılma özelliğini kullanarak ilk parantezi ikinci parantezle çarpmamız yeterlidir:
![Rendered by QuickLaTeX.com \begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-346d3d7ca4da1e71fad52c84a33ef4fc_l3.png)
Şimdi benzer terimleri bir arada gruplandırıyoruz:
![]()
Ve böylece olağanüstü eşitliğin ifadesine ulaştık. Böylece bu dikkat çekici kimlik türünün formülü ortaya çıkıyor:
![]()
Böylece, iki niceliğin farkının toplamının çarpımı, bu niceliklerin karelerinin farkına eşittir. Veya başka bir deyişle, iki farklı terimin toplamını aynı iki terimi çıkararak çarpmak, her iki terimin karesini alıp çıkarmaya eşdeğerdir.
Örnek:
- Karşılık gelen formülü kullanarak, iki farklı terimin farkına göre toplamın aşağıdaki dikkate değer çarpımını bulun:
![]()
Yukarıda gördüğümüz gibi, bir toplamın farkla çarpılmasının dikkate değer eşitliğinin formülü aşağıdaki gibidir:
![]()
Öncelikle yapmamız gereken harflerin değerlerini tespit etmek
![]()
Ve
![]()
formülü. Bu durumda
![]()
değişkene karşılık gelir
![]()
Ve
![]()
2 numaraya karşılık gelir.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-87b76b09924467ba75f033336e6a18e5_l3.png)
Ve parametrelerin hangi değerleri aldığını zaten bildiğimizde
![]()
Ve
![]()
Toplamın çarpımına ilişkin formülü farkla uygularız:
bir üçlünün karesi
Bir trinomiyalin (3 terimden oluşan polinom) karesi , birinci terimin karesi artı ikinci terimin karesi artı üçüncü terimin karesi artı birincinin iki katı ile ikincinin artı birincinin iki katına eşittir. üçüncüsü artı üçüncüsü için ikincinin iki katı.

Herhangi bir üçlü kareden:
![]()
Yukarıdaki kare üç terimlinin kendisi ile çarpılmasında dikkate alınabilir:
![]()
Şimdi polinom çarpımını çözüyoruz:
![]()
Ve son olarak benzer terimleri gruplandırıyoruz:
![]()
Bu şekilde, formülün ifadesine zaten ulaştık, böylece bir üç terimlinin karesi formülü gösterilmiştir:
![]()
Örnek:
- Aşağıdaki dikkate değer eşitliği bulun:
![]()
Üç terimlinin karesinin formülü şöyledir:
![]()
Dikkate değer tüm eşitliklerde olduğu gibi, öncelikle formüldeki bilinmeyenlerin değerlerini belirlemelisiniz. Bu alıştırmada
![]()
Doğu
![]()
katsayı
![]()
karşılık gelir
![]()
Ve
![]()
bağımsız terim 3’tür:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55e06f44486e75e9153a60d36e83bc37_l3.png)
Değerleri zaten bildiğimizde, bu değerleri formülde yerine koyup hesaplamaları yapmanız yeterlidir:

Önemli kimlikler (veya ürünler) küp şeklinde
Az önce tüm kayda değer kimliklerin karesini, yani 2’ye yükseltilmiş kuvvetler tarafından oluşturulan tüm dikkate değer kimlik türlerini inceledik. Şimdi dikkate değer kimlikleri küp şeklinde analiz edeceğiz. Elbette küp özdeşlik formülleri biraz daha karmaşıktır ama aynı zamanda çok faydalıdır.
bir toplamın küpü
Bir toplamın dikkate değer küp çarpımı, iki elemanı pozitif olan bir binomun (yalnızca iki tek terimli polinom) üzeri 3’tür. Bu nedenle cebirsel olarak bir toplamın küpü (a+b) 3 olarak ifade edilir.
Bir toplamın küpünün dikkate değer eşitliğinin formülü şöyledir:

Pozitif bir binom küpünden başlayarak:
![]()
Yukarıdaki güç faktörün çarpımına dahil edilebilir.
![]()
karesine göre:
![]()
Benzer şekilde, dikkate değer karesel eşitliklerde gördüğümüz gibi, binom
![]()
Bir toplamın karesi formülüyle çözülebilir:
![]()
Daha sonra iki polinomu birlikte çarparız:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06771ecbb13542eae2a68477f849d729_l3.png)
Son olarak benzer terimleri bir arada gruplamamız gerekiyor:
![]()
Ve böylece toplam binom küpünün dikkate değer özdeşliği formülü doğrulanır:
![]()
Kısacası, 3’e çıkan bir toplam, birincinin küpü artı birincinin karesinin üç katı ile ikincinin artı birincinin üç katı ikincinin karesi artı ikincinin küpüne eşittir.
Örnek:
- İlgili formülü kullanarak bir küp toplamının aşağıdaki dikkate değer kimliğini çözün:
![]()
Bu problemde iki terimi pozitif olan 3’ün kuvveti bir binomumuz var. Bu nedenle küp toplamı için formülü kullanmalıyız:
![]()
Şimdi parametrelerin değerini bulmamız gerekiyor.
![]()
Ve
![]()
formülü. Bu durumda,
![]()
değişkene karşılık gelir
![]()
Ve
![]()
2 numaradır.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-909b3b4a2f976c165f160a6765b3ed9d_l3.png)
Değerlerini değiştirerek dikkate değer ürünü hesapladığımız
![]()
ve
![]()
formülde:

farkın küpü
Bir farkın küpü veya bir çıkarmanın küpü , negatif işaretli bir terime sahip olan 3’ün kuvveti bir binomdur. Yani bu dikkat çekici ürün tipinin matematiksel ifadesi (ab) 3’tür .
Bir farkın (veya çıkarmanın) küpünün formülü şöyledir:

Açıkçası, bu formülün ispatı toplamın küpü dikkate değer çarpımına çok benzer. Ancak bu durumda negatif küplü binomdan başlıyoruz:
![]()
Açıkça, önceki potansiyelleşme faktörün çarpımına ayrıştırılabilir.
![]()
karesi ile çarpılır:
![]()
Dikkate değer karesel özdeşlikler üzerinde çalıştığımız gibi, binom
![]()
Farkın karesi formülüyle hesaplanabilir:
![]()
Şimdi iki polinomun çarpımını üretiyoruz:
![Rendered by QuickLaTeX.com \begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-627a273de8fff974f4a14a32fcee90b8_l3.png)
Son adım ise benzer terimleri gruplandırmaktır:
![]()
Böylece küp haline getirilen çıkarılmış bir binomun kayda değer kimliğine ilişkin formül doğrulanır:
![]()
Yani üçe çıkarılan bir fark (veya çıkarma) birincinin küpüne eşittir, eksi üç çarpı birincinin karesi çarpı ikinci, artı üç çarpı birincinin karesi ikincinin karesi eksi ikincinin küpü.
Örnek:
- İlgili formülü kullanarak bir sonraki küp binomunu (farkını) hesaplayın:
![]()
Bu alıştırmada bir pozitif ve bir negatif öğeye sahip bir çiftimiz var. Bu nedenle farkın küpü için formülü kullanmalıyız:
![]()
Öncelikle her zaman olduğu gibi bilinmeyenlerin değerini belirliyoruz.
![]()
Ve
![]()
formülü. Bu durumda
![]()
monomial’i temsil eder
![]()
Ve
![]()
binomun bağımsız terimidir, yani 2.
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a792ec6dead8466ec6a2cb2a43d9fab4_l3.png)
Parametrenin
![]()
sayının negatif işareti olmadan basitçe 2’ye eşittir. Formülü doğru bir şekilde uygulamak için bunu akılda tutmak önemlidir.
Son olarak değerleri ortaya koyarak dikkat çekici kimliği buluyoruz.
![]()
ve
![]()
formülde:

Önemli kimliklerin özet tablosu
Özetle, gördüğümüz tüm önemli kimlikleri (veya ürünleri) içeren bir tablo hazırladık, böylece bunları incelemeniz daha kolay olacaktır. 😉

Önemli kimliklere (veya ürünlere) ilişkin çözülmüş alıştırmalar
Dikkat çekici ürünler veya dikkate değer eşitlikler olarak da adlandırılan dikkate değer kimlikler kavramını anlamayı tamamlamanız için, adım adım çözülen birkaç alıştırma hazırladık. Bunları yapmayı deneyebilir ve ardından alıştırmaların çözümleriyle iyi iş çıkarıp çıkarmadığınızı kontrol edebilirsiniz.
⬇⬇ Tüm sorularınızı aşağıda yorum olarak bize sorabileceğinizi unutmayın! ⬇⬇
1. Egzersiz
Aşağıdaki dikkate değer kimlikleri genişletin (karelerin toplamı):
![]()
![]()
![]()
![]()
Sorundaki tüm dikkate değer özdeşliklerin kareleri alınmış toplamlardır, dolayısıyla bu durumda her zaman aynı formülü uygulamamız gerekir:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-067fdf38612ca481db587bda479cab24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Alıştırma 2
Aşağıdaki dikkate değer ürünleri geliştirin (farklılıkların kareleri):
![]()
![]()
![]()
![]()
Bu alıştırmada dikkate değer tüm çarpımlar kare çıkarma işlemidir, dolayısıyla yalnızca tek bir formül uygulamamız gerekir:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14d502eda968fe82617b4403cd9c4722_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c22d520301280872e645f5683a2fba8e_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95c7c481a96b20b700bd2253c90f0c0d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cea9fa89580d3d9d9df7fd93cca2b89_l3.png)
Alıştırma 3
Aşağıdaki dikkate değer eşitlikleri geliştirin (toplamların farklara göre çarpımı):
![]()
![]()
![]()
![]()
Bu alıştırmadaki tüm dikkate değer eşitlikler, toplamların farklarla çarpımı olduğundan, hepsi aynı formülle çözülür:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-826c4aec8f005514a14cdc8555c084c4_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6793239af84413fb9408c2cb6033e5ce_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-630b94cf4be27c5f7b9c87651368634d_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-80c5451e407a2c0e670c6cb22a74043c_l3.png)
Alıştırma 4
Aşağıdaki dikkate değer kimliklerin tümünü çözümleyin:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c65875e01d82840e30ae85d803d45e90_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04e0bcf5df362d320cfdb2f87cdc6ddc_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cc3f7dc61f7c44a60c01e0a95de278fa_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4d4a0c86d26820881eb65cb92c3679a_l3.png)
![Rendered by QuickLaTeX.com \text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-432c4ae0f050bec15e3fa52f426698ec_l3.png)
Alıştırma 5
Aşağıdaki önemli ürünleri hesaplayın:
![]()
![]()
![]()
![]()
Sorunun tüm dikkate değer ürünlerini bulmak için, bir toplam ve farkın küpü için formülleri durumlara göre uygulamak gerekir:
![]()
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-14695fb807e2df89352fdd1c1dced2ee_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5be0d584351feb0bef5572ca5c9e159a_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44f9c3283dad97321644c6e559f64ff_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-156e7619e4d6ef129f04250af8197d2e_l3.png)
Alıştırma 6
Aşağıdaki önemli eşitlikleri çözün:
![]()
![]()
![]()
![]()
Tüm bu dikkate değer özdeşlikleri çözmek için üç terimlinin karesi formülünü kullanmamız gerekir:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-749dc45e7a00d7122d62b774706bdcc0_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1f51f18b3c1118b6e8e3acc3441b0ec_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-49c6496bf684296d315fc96d9cb5857e_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7cd08035d8402c27c411bcf5b30216cb_l3.png)
Egzersiz 7
Aşağıdaki dikkate değer özdeşlikleri kökler ve kesirlerle hesaplayın (yüksek zorluk):
![]()
![]()
![]()
![]()
Bölüm A) kareli bir çıkarma işleminden oluşur, bu nedenle bunu çözmek için karşılık gelen formülün uygulanması gerekir ve ayrıca, eğer bir kökün karesi alınırsa basitleştirildiği de unutulmamalıdır:
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-999e71bf062ea313780439abaf2b4295_l3.png)
Bölüm B) çıkarma yoluyla toplama ile ilgilidir ve monomiyallerin kesirli katsayıları vardır; bu önemli çarpımın, çıkarma yoluyla toplama formülü ve kesirlerin özellikleri kullanılarak belirlenmesi gerekir:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24593bac7bd4a9837e1f18fef4f9c38e_l3.png)
Bölüm C)’deki dikkate değer eşitlik, 2’ye yükseltilmiş bir toplamdır ve aynı şekilde kesirlerden oluşur. Bu nedenle, bunu hesaplamak için kare toplamının formülünü artı kesirlerin özelliklerini kullanmamız gerekir:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Dikkate değer son özdeşlik, irrasyonel katsayılarla toplam çarpı farkla ilgilidir, bu nedenle formülü toplam çarpı fark için uygularız ve ardından karekökleri basitleştiririz:
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c540e4315e9e84faaa2ff656c4eec21_l3.png)
Diğer önemli kimlik türleri
Yukarıda tartıştığımız tüm önemli kimlikler en sık kullanılanlardır. Ancak matematikte farklı amaçlarla kullanıldıkları için bilinmesi gereken başka önemli ürün türleri de vardır.
küplerin toplamı
Küplerin toplamı, iki terimi pozitif olan ve üstelik kübik kökleri tam olan bir binoma karşılık gelir. Bu nedenle küplerin toplamının cebirsel ifadesi a 3 +b 3’tür .

Bu dikkate değer çarpımın formülü bir polinomu çarpanlara ayırmak için kullanılır, yani formül aracılığıyla bir polinomu bir binomun bir trinomial çarpımına dönüştürürüz.
Nasıl yapıldığını görebilirsiniz, işte bu dikkat çekici kimliğin örnek bir uygulaması:
![]()
Aslında önceki ifade küplerin eklenmesinden oluşur çünkü tek terimlinin kübik kökü
![]()
kesindir (ondalık sayı vermez) ve 8 sayısı da:
![]()
![]()
![]()
Bu nedenle, kübik ifadeyi bir binomun bir trinomial çarpımına dönüştürmek için mükemmel küplerin toplamı formülünü kullanabiliriz:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f30ea5f0f7ef1b89a16f1d00e54d063c_l3.png)
küp farkı
Küplerin farkı (veya çıkarılması), kübik kökleri kesin olan bir pozitif terim ve bir negatif terimden oluşan bir binomdur. Başka bir deyişle küp farkı a 3 -b 3 şeklinde ifade edilir.

Bu dikkat çekici kimlik tipinin nasıl çözüldüğünü görebilmeniz için bir örnek yapalım:
![]()
Bu bir küp farkıdır çünkü hem tek terimlinin kübik kökü
![]()
27 doğru olduğundan:
![]()
![]()
![]()
Bu nedenle, binom çarpanlarına ayırmak için mükemmel küplerin farkı formülünü kullanabilirsiniz:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-342a448f849bf2856ad9a5394733faeb_l3.png)
Ortak terimli binomların çarpımı
Bu dikkate değer çarpım, ortak bir terime sahip iki binomun çarpımını ikinci dereceden bir polinoma dönüştürmek için kullanılır.

İşte bu tür olağanüstü ürünün ayrıntılı bir örneği:
![Rendered by QuickLaTeX.com \begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8447db6a2246c09b2e7be29f8050a3d6_l3.png)
daha fazla kimlik
Dikkate değer kimlikler en yaygın oldukları için en ünlüleri olsa da, başka isimlerle de kimliklerin daha fazla olduğunu belirtmek gerekir. Merak ediyorsanız, daha az bilinen diğer kimliklerin bir listesi:
- Lagrange özdeşlikleri:
-
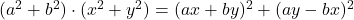
-
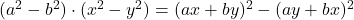
- Efsanevi kimlikler:
-
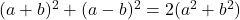
-
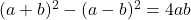
-
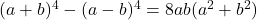
- Argand’ın kimliği:
-
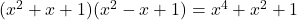
- Gauss kimlikleri:
-
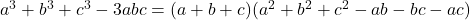
-
![Rendered by QuickLaTeX.com a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6b2da7d99ade85355a54bee45b79a9f_l3.png)
Önemli kimlik uygulamaları
Eğer bu noktaya kadar geldiyseniz, kayda değer kimliklerle hesaplamaların nasıl yapılacağını zaten biliyorsunuz demektir. Parlak! Ama gerçekten… dikkate değer kimlikler ne işe yarar? Peki dikkate değer kimlikler ne zaman kullanılır?
Bu makale boyunca gördüğümüz gibi dikkate değer kimliklerin temel amacı hesaplamaları basitleştirmektir. Yani dikkat çekici ürünler sayesinde karmaşık polinomların belirli kuvvetlerini zor işlemlere gerek kalmadan doğrudan çözebiliyoruz.
Ancak dikkate değer eşitliklerin polinomları çarpanlara ayırma ve karelere tamamlama gibi başka işlevleri de vardır. Daha sonra bu uygulamaların her birinin nelerden oluştuğunu göreceğiz.
Polinomları çarpanlara ayırma
Bazı çok özel polinom türleri dikkate değer özdeşliklerle çarpanlara ayrılabilir. Örneğin, tam kare olan iki terimden oluşan bir polinom bulursak (karekökleri tamdır), bir toplamın farkla çarpımına ilişkin dikkate değer eşitlik formülünü kullanarak bunu çarpanlarına ayırabiliriz:
![]()
![]()
Benzer şekilde, bir toplama veya çıkarma işleminin karesinin dikkate değer kimliklerine saygı duyan üç terimli sayılar çarpanlara ayrılabilir:
![]()
![]()
![]()
![]()
Benzer şekilde, bir polinom çarpanlara ayrıldıktan sonra o polinomun kökleri (veya sıfırları) bulunabilir. Öyle bile olsa, bu kavramın anlaşılması biraz daha karmaşıktır, bu nedenle daha fazla ilgileniyorsanız, açıklamayı web sitemizdeki (sağ üstte) arama motorunda aramanızı öneririz, çünkü bunu açıklayan tam bir makalemiz var.
kare tamamlama
Karelere tamamlama, ikinci dereceden bir üç terimliyi bir karenin artı (veya eksi) bir sayının toplamına dönüştürmek için kullanılan matematiksel bir prosedürdür.
Herhangi bir trinomial verildiğinde:
![]()
Daha sonra trinomial aşağıdaki ifadeye dönüştürülebilir:
![]()
parametreler nerede
![]()
Ve
![]()
aşağıdaki formüllerle hesaplanır:
![]()
Size pek öyle gelmese de bu iki formül dikkat çeken kimliklerden çıkarılıyor. Böylece dikkat çeken ürünler sayesinde kareler tamamlanabiliyor.
Örnek olarak, bu prosedürü aşağıdaki üç terimliye uygulayacağız:
![]()
Parametreleri hesaplıyoruz
![]()
Ve
![]()
![]()
![]()
Ve bu nedenle polinom kalır:
![]()