İdempotent matris

Bu sayfada idempotent matrislerin ne olduğunu açıklıyoruz. Tamamen anlamanız için size bu tür matrislerin birkaç örneğini de gösteriyoruz. Ayrıca, idempotent bir matris bulma formülünü ve son olarak da idempotent matrislerin tüm özelliklerini bulacaksınız.

İdempotent matris nedir?

İdempotent bir matrisin tanımı aşağıdaki gibidir:

İdempotent bir matris , kendisiyle çarpıldığında sonuç olarak aynı matrisi veren matristir.

$A\cdot A = A$

Bu nedenle, idempotent bir matrisin herhangi bir gücü , üsse bakılmaksızın matrisin kendisine eşittir:

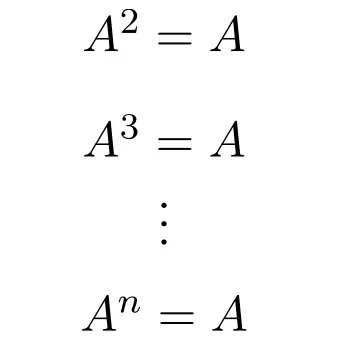
Aslında bu tür tahtaların ismini almasının nedeni de budur. Çünkü matematikte eşpotanslık bir işlemdir, yani kaç kez yapılırsa yapılsın her zaman aynı sonucu elde ederiz.

İdempotent matris örnekleri

İdempotent matris kavramını öğrendikten sonra, onu anlamayı tamamlamak için farklı boyutlardan bazı örnekler göreceğiz.

2×2 idempotent matris örneği

Aşağıdaki 2×2 boyutlu kare matris idempotenttir:

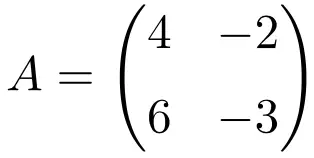
2x2 boyutunda idempotent bir matris örneği

İdempotent bir matris olduğunu doğrulamak için karesini hesaplıyoruz:

$\displaystyle A^2=\begin{pmatrix} 4 &-2 \\[1.1ex] 6 & -3 \end{pmatrix}$

Sonuç aynıdır, dolayısıyla bunun idempotent bir matris olduğunu gösteriyoruz.

3×3 idempotent matris örneği

Aşağıdaki 3×3 boyutunda kare matris idempotenttir:

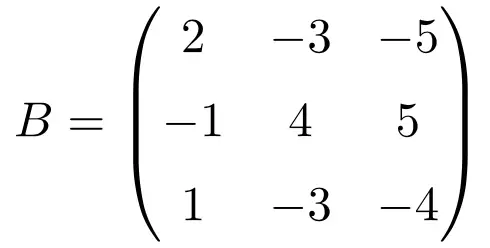
3x3 boyutunda idempotent bir matris örneği

İdempotent bir matrisin karşılık gelip gelmediğini kontrol etmek için matrisi 2’ye yükseltiriz:

$\displaystyle B^2=\begin{pmatrix} 2 &-3 & -5 \\[1.1ex] -1 & 4 & 5 \\[1.1ex] 1 & -3 & -4 \end{pmatrix}$

Sonuç orijinal matrisle aynıdır, dolayısıyla matrisin önemsizliği kanıtlanmıştır.

2 × 2 idempotent matrisin yapısı

Burada size idempotent bir matris elde etmenin formülünü gösteriyoruz. Daha fazla ilgileniyorsanız, yorumlarda aşağıdaki formülün gösterimini görebilirsiniz, ancak bu biraz sıkıcı olduğundan burada sizi doğrudan idempotent matris formülüyle baş başa bırakıyoruz:

Öyle ki, bir idempotent matrisin ikincil köşegeninin elemanları, koşul karşılandığı sürece keyfi olabilir.

$a^2+bc=a$

ve ana köşegendeki sayılar şu şekilde olmalıdır:

$a$

$1-a.$

Bu formülle açıklanan tüm matrislere ek olarak, formüle uymamasına rağmen aynı zamanda idempotent bir matris olan Kimlik matrisini de eklemeliyiz. Dizinin ne olduğunu bilmiyorsanız Kimlik dizisinin ne olduğunu sorabilirsiniz.

İdempotent matrislerin özellikleri

İdempotent matrisler aşağıdaki özelliklere sahiptir:

İdempotent bir matrisin determinantı her zaman 0 veya 1’dir.

Birim matrisi dışındaki tüm diğer idempotent matrisler hem tekil hem de dejenere matrislerdir, yani tersinir değildirler.

Herhangi bir idempotent matris köşegenleştirilebilir ve özdeğerleri (veya özdeğerleri) her zaman 0 veya 1’dir.

İdempotent bir matrisin izi, matrisin rütbesine eşittir.

Son olarak, idempotent matrisler ile evrimsel matrisler arasında bir ilişki vardır: matris
$A$

idempotenttir ancak ve ancak matris

$\displaystyle P= 2A-I$

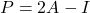
bu involüsyoneldir.

İdempotent matris